TI/Uczenie maszynowe: Różnice pomiędzy wersjami
| Linia 19: | Linia 19: | ||
W najprostzym sformułowaniu uczenie maszynowe to zbiór metod statystycznych, które na podstawie danych uczących (doświadczenie) tworzą algorytmy pozwalające klasyfikować dane, których w zbiorze uczącym nie było. Można je próbować dobrać na podstawie posiadanych danych tak, żeby dla osób, które wcześniej nie spłacały kredytów, równanie dawało wartości ujemne, a dla spłacających regularnie — dodatnie. Nawet w tak drastycznie uproszczonym przykładzie mamy sześć zmiennych A--D — uprośćmy go jeszcze bardziej, do dwóch zmiennych "obciążenia" i "majątek". Wtedy dane każdej osoby, której bank kiedyś udzielił kredytu, można przedstawić w dwóch wymiarach, czyli na płaszczyźnie. Dane osób, które spłacały, oznaczymy zielonym, a pozostałych — czerwonym kolorem: | W najprostzym sformułowaniu uczenie maszynowe to zbiór metod statystycznych, które na podstawie danych uczących (doświadczenie) tworzą algorytmy pozwalające klasyfikować dane, których w zbiorze uczącym nie było. Można je próbować dobrać na podstawie posiadanych danych tak, żeby dla osób, które wcześniej nie spłacały kredytów, równanie dawało wartości ujemne, a dla spłacających regularnie — dodatnie. Nawet w tak drastycznie uproszczonym przykładzie mamy sześć zmiennych A--D — uprośćmy go jeszcze bardziej, do dwóch zmiennych "obciążenia" i "majątek". Wtedy dane każdej osoby, której bank kiedyś udzielił kredytu, można przedstawić w dwóch wymiarach, czyli na płaszczyźnie. Dane osób, które spłacały, oznaczymy zielonym, a pozostałych — czerwonym kolorem: | ||
| − | [[Plik:LDA bank2.png| | + | [[Plik:LDA bank2.png|500px|bezramki]] |
Pozostaje wykreśli linię, oddzeilającą te dwie grupy. Nowy kandydat na kredytobiorcę po wypełnieniu informacji staje się punktem w tej przestrzeni. Jeśli punkt znajdzie się pod kreską, bank udzieli kredytu. | Pozostaje wykreśli linię, oddzeilającą te dwie grupy. Nowy kandydat na kredytobiorcę po wypełnieniu informacji staje się punktem w tej przestrzeni. Jeśli punkt znajdzie się pod kreską, bank udzieli kredytu. | ||
Jak widać przykład na powyższym rysunku, zwykle nie da się poprowadzić linii tak, żeby wszyscy dotychczasowi klienci znaleźli się "po właściwej stronie". Oczywiście można by do danych uczących dopasować łamaną lub wielomian, który rozdzielał by znane przypadki w sposób idealny. | Jak widać przykład na powyższym rysunku, zwykle nie da się poprowadzić linii tak, żeby wszyscy dotychczasowi klienci znaleźli się "po właściwej stronie". Oczywiście można by do danych uczących dopasować łamaną lub wielomian, który rozdzielał by znane przypadki w sposób idealny. | ||
| + | [[Plik:LDA bank.003.png|500px|bezramki]] | ||
| − | [[ | + | Ale doskonałe rozdzielenie przypadków w zbiorze uczącym nie musi oznaczać, że nowi klienci będą klasyfikowani prawidłowo — ta cecha określana jest zdolnością do generalizacji (wiedzy, nabytej na podstawie zbioru uczącego, na nowe przypadki, których w tym zbiorze nie było). Jej optymalizacja jest głownym celem tej części statystyki. Z niektórymi technikami zapoznamy się na wykładzie z [[Sztuczne_sieci_neuronowe_(ANN_)|Wnioskowania Statystycznego]]. |
Wersja z 13:56, 18 lip 2024
Przykład: ocena zdolności kredytowej
Przed udzieleniem kredytu bank ocenia tzw. zdolność kredytową potencjalnego kredytobiorcy. Chodzi konkretnie o prawdopodobieństwo tego, że kredyt będzie spłacany. Tradycyjnie decyzje takie podejmowali doświadczeni urzędnicy, na podstawie:
- danych potencjalnego kredytobiorcy — na przykład takich, jak na powyższym rysunku
- doświadczenia opartego na faktycznej spłacalności udzielanych wcześniej kredytów.
Jeśli "doświadczenie" potraktujemy jako wiedzę nabytą przez konkretnego urzędnika, decyzja będzie mniej lub bardziej subiektywna — na przykład lepsze wrażenie zrobi być może osoba w drogim garniturze, co niekoniecznie musi wpływać na faktyczną zdolność kredytową. Dlatego w szukamy coraz bardziej obiektywnych metod, opartych na konkretnych danych. Bank mógłby spisać doświadczenia wszystkich urzędników w postaci reguł typu "osoba bez stałego zatrudnienia, pomimo wysokiego stanu gotówki na kontach jest potencjalnym kłopotem, kredytu nie udzielamy".
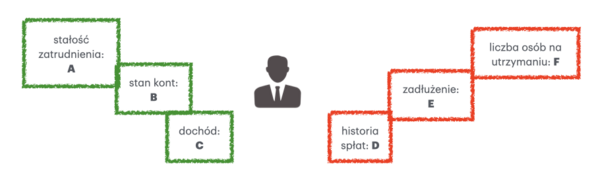
Żeby proces był całkowicie obiektywny, możemy go zalgorytmizować, czyli przedstawić w formie algorytmu. Po przypisaniu wartości liczbowych parametrom A, B, C, D, E i F, mógłby on wyglądać na przykład tak:
- oblicz [math]x = w_1 A +w_2 B + w_3 C - w_4 D - w_5 E - w_6 F[/math]
- jeśli [math]x \geq 0[/math], przyznaj kredyt, koniec
- jeśli [math]x\lt 0[/math], odmów kredytu, koniec
Skąd wziąć wartości współczynników (wag) [math] w_i[/math], określających względne znaczenie poszczególnych parametrów? Oczywiście z doświadczenia. Ale jak? Tu z pomocą przychodzi statystyka.
Uczenie maszynowe
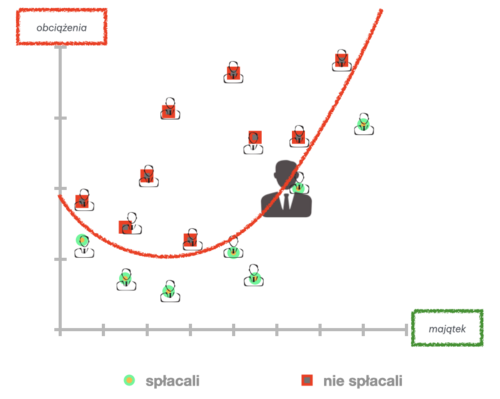
W najprostzym sformułowaniu uczenie maszynowe to zbiór metod statystycznych, które na podstawie danych uczących (doświadczenie) tworzą algorytmy pozwalające klasyfikować dane, których w zbiorze uczącym nie było. Można je próbować dobrać na podstawie posiadanych danych tak, żeby dla osób, które wcześniej nie spłacały kredytów, równanie dawało wartości ujemne, a dla spłacających regularnie — dodatnie. Nawet w tak drastycznie uproszczonym przykładzie mamy sześć zmiennych A--D — uprośćmy go jeszcze bardziej, do dwóch zmiennych "obciążenia" i "majątek". Wtedy dane każdej osoby, której bank kiedyś udzielił kredytu, można przedstawić w dwóch wymiarach, czyli na płaszczyźnie. Dane osób, które spłacały, oznaczymy zielonym, a pozostałych — czerwonym kolorem:
Pozostaje wykreśli linię, oddzeilającą te dwie grupy. Nowy kandydat na kredytobiorcę po wypełnieniu informacji staje się punktem w tej przestrzeni. Jeśli punkt znajdzie się pod kreską, bank udzieli kredytu.
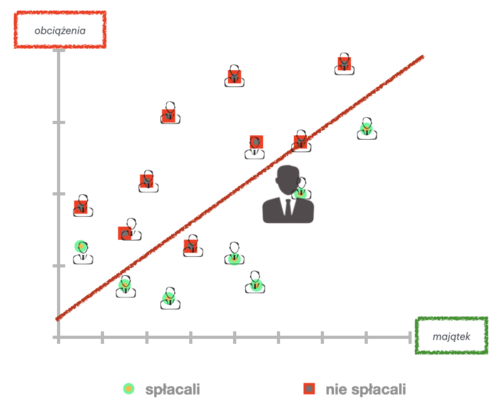
Jak widać przykład na powyższym rysunku, zwykle nie da się poprowadzić linii tak, żeby wszyscy dotychczasowi klienci znaleźli się "po właściwej stronie". Oczywiście można by do danych uczących dopasować łamaną lub wielomian, który rozdzielał by znane przypadki w sposób idealny.
Ale doskonałe rozdzielenie przypadków w zbiorze uczącym nie musi oznaczać, że nowi klienci będą klasyfikowani prawidłowo — ta cecha określana jest zdolnością do generalizacji (wiedzy, nabytej na podstawie zbioru uczącego, na nowe przypadki, których w tym zbiorze nie było). Jej optymalizacja jest głownym celem tej części statystyki. Z niektórymi technikami zapoznamy się na wykładzie z Wnioskowania Statystycznego.
