Wstep: Różnice pomiędzy wersjami
| Linia 28: | Linia 28: | ||
===Sygnał dyskretny jako wektor=== | ===Sygnał dyskretny jako wektor=== | ||
| − | [[Plik:AD.png| | + | [[Plik:AD.png|mały|220px|<pre>102, 195, 80, 16, 147, 178</pre>]] |
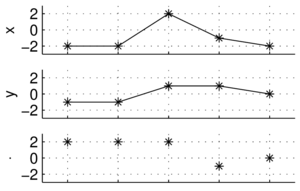
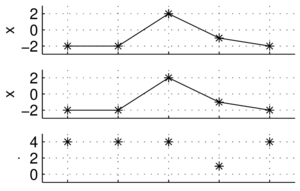
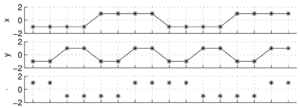
| − | + | Skoro sygnał to po prostu jako ciąg liczb, możemy go potraktować jak wektor. Na płaszczyźnie wektor to para współrzędnych (''x'', ''y''). | |
| + | Dzięki temu możemy korzystać z 'gotowych' pojęć z dziedziny algebry wektorów, jak ortogonalność czy iloczyn skalarny, który możemy przyjąć jako miarę podobieństwa dwóch sygnałów. | ||
| + | |||
| + | |||
| − | |||
| − | |||
| Linia 47: | Linia 48: | ||
[[Plik:Product6.png|bezramki]] | [[Plik:Product6.png|bezramki]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | [https://en.wikipedia.org/wiki/Energy_(signal_processing) Energia sygnału] | ||
===Liczby zespolone=== | ===Liczby zespolone=== | ||
Wersja z 09:28, 27 lip 2024
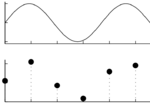
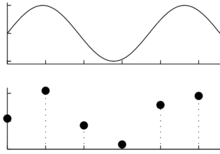
Sygnały zapisujemy, przetwarzamy i analizujemy w postaci ciągów liczb. Przejście od sygnału ciągłego do cyfrowego odbywa się przez proces próbkowania, czyli zapisywania kolejnych amplitud sygnału w ustalonych, stałych odstępach czasu, omawiany wcześniej na TIiK.
Ciągły sygnał z górnego rysunku, po próbkowaniu w punktach symbolizowanych czarnymi kropkami na rysunku dolnym, na dysku zostaje zapisany jako ciąg liczb:
102, 195, 80, 16, 147, 178
Żeby odtworzyć fizyczne własności sygnału, czyli narysować zapisane wartości próbek (czarne kropki) w odpowiedniej skali, musimy znać częstość próbkowania i stałą kalibracji.
Wyrażana w hercach (Hz) częstość próbkowania (ang. sampling frequency, [math]f_s[/math]) to liczba próbek na sekundę. Jest ona odwrotnością odstępu w czasie między kolejnymi próbkami ([math]\Delta t[/math]):
[math]f_s = \dfrac{1}{\Delta t}[/math]
Stała kalibracji to współczynnik, przez który mnożymy zapisane liczby, żeby otrzymać wartości w jednostkach fizycznych, na przykład mikrowoltach.
Oczywiście musimy też wiedzieć, w jakim formacie zapisano na dysku liczby (omawiany rok temu na wykładzie o binarnych reprezentacjach liczb), oraz, w przypadku sygnałów wielozmiennych o jednolitym próbkowaniu, znać liczbę kanałów. Taka dodatkowa informacja (metainformacja) jest konieczna do poprawnego wyświetlenia danych z pliku.
Aliasing
Poza znajomością zależności między zapisanymi liczbami a jednostkami fizycznymi w procesie próbkowania kluczową rolę odgrywa twierdzenie o próbkowaniu (inaczej twierdzenie Nyquista-Shannona, czasem w skrócie twierdzenie Nyquista). Mówi ono, że sygnał ciągły możemy odtworzyć za zapisanych próbek, jeśli częstość próbkowania [math]f_p[/math] była wyższa niż dwukrotność najwyższej z występujących w sygnale częstości [math]f_{max}[/math], nazywana częstością Nyquista [math]f_N[/math]:
[math] f_s = \dfrac{1}{\Delta t} \gt 2* f_{max} = f_N[/math]
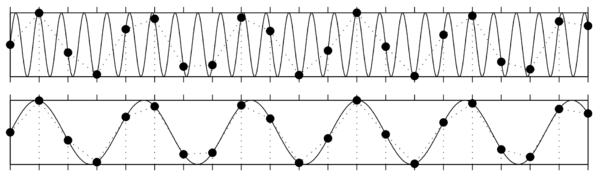
Jeśli częstość próbkowania nie była wystarczająco wysoka, nie tylko stracimy informację o zmianach amplitudy sygnału "pomiędzy próbkami", ale dojdzie też do zafałszowania sygnału w niższych częstościach, które z pozoru nie powinny być zaburzone. Efekt ten jest bliżej omówiony w rozdziale Aliasing.
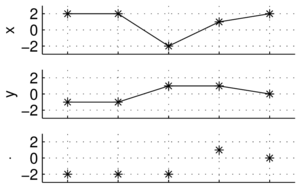
Sygnał dyskretny jako wektor
Skoro sygnał to po prostu jako ciąg liczb, możemy go potraktować jak wektor. Na płaszczyźnie wektor to para współrzędnych (x, y). Dzięki temu możemy korzystać z 'gotowych' pojęć z dziedziny algebry wektorów, jak ortogonalność czy iloczyn skalarny, który możemy przyjąć jako miarę podobieństwa dwóch sygnałów.