Wstep: Różnice pomiędzy wersjami
| Linia 43: | Linia 43: | ||
<math>y=[-1, -1, 1, 1, 0]</math> | <math>y=[-1, -1, 1, 1, 0]</math> | ||
| − | + | Zamiast strzałek w pięciowymiarowej przestrzeni, łatwiej wizualizować na wykresach wartości kolejnych próbek: | |
[[Plik:Product2.png|bezramki]] | [[Plik:Product2.png|bezramki]] | ||
<math>x\cdot y = [-2, -2, 2, -1, -2] \cdot [-1, -1, 1, 1, 0] = 2+2+2-1+0 = 5</math> | <math>x\cdot y = [-2, -2, 2, -1, -2] \cdot [-1, -1, 1, 1, 0] = 2+2+2-1+0 = 5</math> | ||
| + | |||
| + | Iloczyn skalarny sygnału z samym sobą, czyli <math>x\cdot x</math>, w analizie sygnałów nazywać będziemy jego energią — jeśli sygnałem będzie np. prąd elektryczny, płynący w obwodzie o jednostkowej oporności, to wytracona przez niego energia wyniesie właśnie <math>x\cdot x</math> | ||
[[Plik:Product3.png|bezramki]] | [[Plik:Product3.png|bezramki]] | ||
| + | |||
| + | <math>x\cdot x = [-2, -2, 2, -1, -2] \cdot [-2, -2, 2, -1, -2] = 4+4+4+1+4=17</math> | ||
| + | |||
| + | Kolejnym użytecznym pojęciem, które możemy zaczerpnąć bezpośrednio z algebry wektorów, jest ortogonalność | ||
[[Plik:Product6.png|bezramki]] | [[Plik:Product6.png|bezramki]] | ||
Wersja z 11:40, 27 lip 2024
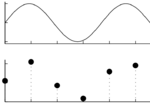
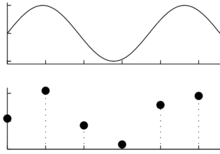
Sygnały zapisujemy, przetwarzamy i analizujemy w postaci ciągów liczb. Przejście od sygnału ciągłego do cyfrowego odbywa się przez proces próbkowania, czyli zapisywania kolejnych amplitud sygnału w ustalonych, stałych odstępach czasu, omawiany wcześniej na TIiK.
Ciągły sygnał z górnego rysunku, po próbkowaniu w punktach symbolizowanych czarnymi kropkami na rysunku dolnym, na dysku zostaje zapisany jako ciąg liczb:
102, 195, 80, 16, 147, 178
Żeby odtworzyć fizyczne własności sygnału, czyli narysować zapisane wartości próbek (czarne kropki) w odpowiedniej skali, musimy znać częstość próbkowania i stałą kalibracji.
Wyrażana w hercach (Hz) częstość próbkowania (ang. sampling frequency, [math]f_s[/math]) to liczba próbek na sekundę. Jest ona odwrotnością odstępu w czasie między kolejnymi próbkami ([math]\Delta t[/math]):
[math]f_s = \dfrac{1}{\Delta t}[/math]
Stała kalibracji to współczynnik, przez który mnożymy zapisane liczby, żeby otrzymać wartości w jednostkach fizycznych, na przykład mikrowoltach.
Oczywiście musimy też wiedzieć, w jakim formacie zapisano na dysku liczby (omawiany rok temu na wykładzie o binarnych reprezentacjach liczb), oraz, w przypadku sygnałów wielozmiennych o jednolitym próbkowaniu, znać liczbę kanałów. Taka dodatkowa informacja (metainformacja) jest konieczna do poprawnego wyświetlenia danych z pliku.
Aliasing
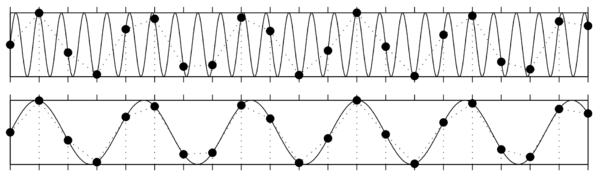
Poza znajomością zależności między zapisanymi liczbami a jednostkami fizycznymi w procesie próbkowania kluczową rolę odgrywa twierdzenie o próbkowaniu (inaczej twierdzenie Nyquista-Shannona, czasem w skrócie twierdzenie Nyquista). Mówi ono, że sygnał ciągły możemy odtworzyć za zapisanych próbek, jeśli częstość próbkowania [math]f_p[/math] była wyższa niż dwukrotność najwyższej z występujących w sygnale częstości [math]f_{max}[/math], nazywana częstością Nyquista [math]f_N[/math]:
[math] f_s = \dfrac{1}{\Delta t} \gt 2* f_{max} = f_N[/math]
Jeśli częstość próbkowania nie była wystarczająco wysoka, nie tylko stracimy informację o zmianach amplitudy sygnału "pomiędzy próbkami", ale dojdzie też do zafałszowania sygnału w niższych częstościach, które z pozoru nie powinny być zaburzone. Efekt ten jest bliżej omówiony w rozdziale Aliasing.
Sygnał dyskretny jako wektor
Skoro sygnał to po prostu ciąg liczb, możemy go potraktować jak wektor. Na płaszczyźnie wektor to para współrzędnych (x, y), w przestrzeni trójwymiarowej trójka liczby (x, y, z), a wektor wyobrażamy sobie jako strzałkę wiodącę od punktu (0, 0, 0) do (x, y, z). Sygnał składający się z pięciu punktów będzie wektorem w przestrzeni pięciowymiarowej, więc intuicja "strzałki" dla większości z nas przestaje być użyteczna. Pomimo tego, możemy możemy wciąż korzystać z użyecznych pojęć z dziedziny algebry wektorów, jak ortogonalność czy iloczyn skalarny.
Iloczyn skalarny przyjmiemy jako miarę podobieństwa dwóch sygnałów. Obliczać go będziemy tak samo jak dla wektorów — przypomnijmy: niech [math]\mathbf{x} = [x_1, x_2, x_3][/math], i [math]\mathbf{y} = [y_1, y_2, y_3][/math]; iloczyn skalarny tych wektorów oznaczamy [math]\mathbf x \cdot \mathbf y[/math] (zarówno wytłuszczenie symboli wektorów, jak i symbol mnożenia/ilocznu skalarnego "[math]\cdot[/math]", będziemy dalej pomijać):
[math]\displaystyle \mathbf a \cdot \mathbf b = \sum_{i=1}^3 x_i y_i = x_1 y_1 + x_2 y_2 + x_3 y_3[/math]
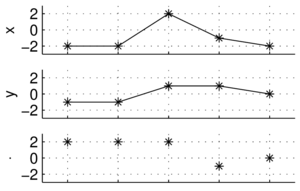
A jak to będzie wyglądać dla sygnałów złożonych z więcej niż trzech punktów? Weźmy
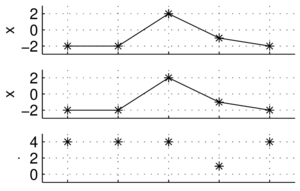
[math]x=[-2, -2, 2, -1, -2][/math]
[math]y=[-1, -1, 1, 1, 0][/math]
Zamiast strzałek w pięciowymiarowej przestrzeni, łatwiej wizualizować na wykresach wartości kolejnych próbek:
[math]x\cdot y = [-2, -2, 2, -1, -2] \cdot [-1, -1, 1, 1, 0] = 2+2+2-1+0 = 5[/math]
Iloczyn skalarny sygnału z samym sobą, czyli [math]x\cdot x[/math], w analizie sygnałów nazywać będziemy jego energią — jeśli sygnałem będzie np. prąd elektryczny, płynący w obwodzie o jednostkowej oporności, to wytracona przez niego energia wyniesie właśnie [math]x\cdot x[/math]
[math]x\cdot x = [-2, -2, 2, -1, -2] \cdot [-2, -2, 2, -1, -2] = 4+4+4+1+4=17[/math]
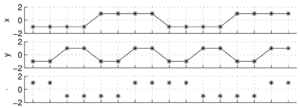
Kolejnym użytecznym pojęciem, które możemy zaczerpnąć bezpośrednio z algebry wektorów, jest ortogonalność