Spektrogram: Różnice pomiędzy wersjami
Z Brain-wiki
| Linia 9: | Linia 9: | ||
</math></center> | </math></center> | ||
| − | Moduł współczynnika <math>c_{\xi, t_0}</math> mówi o zawartości energii sygnału <math>s(t)</math> w okolicy częstości <math>\xi</math> i czasu <math>t_0</math> (rys. <xr id="fig:6"> %i</xr>). | + | Moduł współczynnika <math>c_{\xi, t_0}</math> mówi o zawartości energii sygnału <math>s(t)</math> w okolicy częstości <math>\xi</math> i czasu <math>t_0</math><!--(rys. <xr id="fig:6"> %i</xr>).--> |
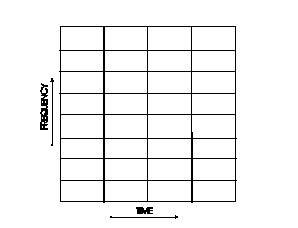
[[Plik:timefreq_rys_3.jpg|thumb|center|400px|<figure id="fig:6"></figure>Równomierny podział przestrzeni czas-częstość dla oknowanej transformaty Fouriera]] | [[Plik:timefreq_rys_3.jpg|thumb|center|400px|<figure id="fig:6"></figure>Równomierny podział przestrzeni czas-częstość dla oknowanej transformaty Fouriera]] | ||
Wersja z 11:12, 3 wrz 2024
AS/ Spektrogram — oknowana transformata Fouriera
Przepis na krótkoczasową transformatę Fouriera (Short-Time Fourier Transform, STFT ) polega na wycinaniu kolejnych odcinków sygnału z pomocą okna [math]g(t)[/math] ([math]\|g\|=1[/math]) i obliczaniu ich transformaty Fouriera. Inaczej można to opisać jako iloczyny skalarne sygnału z oknem [math]g[/math] modulowanym częstością [math]\xi[/math]:
Moduł współczynnika [math]c_{\xi, t_0}[/math] mówi o zawartości energii sygnału [math]s(t)[/math] w okolicy częstości [math]\xi[/math] i czasu [math]t_0[/math]