
TI/Programowanie dla Fizyków Medycznych/Optymalizacja: Różnice pomiędzy wersjami
Z Brain-wiki
| Linia 1: | Linia 1: | ||
==Optymalizacja jednowymiarowa== | ==Optymalizacja jednowymiarowa== | ||
| + | Omawianie zagadnienia optymalizacji rozpocznijmy od prostego przykładu. Zdefiniujmy pewną funkcję i zobaczmy jak wygląda jej wykres. | ||
| + | <source lang="python"> | ||
| + | import numpy as np | ||
| + | import pylab as py | ||
| − | |||
licznikTestowej=0 | licznikTestowej=0 | ||
| Linia 16: | Linia 19: | ||
[[Plik:opt1.png]] | [[Plik:opt1.png]] | ||
| + | Na rozważanym przedziale [0.2,2] powyższa funkcją ma tylko jedno ekstremum lokalne. Taką funkcję nazywamy unimodalną. Zmienna licznikTestowej umożliwi nam zliczać wywołania funkcji testowej przez analizowane procedury. | ||
| + | Zagadnienie którym teraz będziemy się zajmować to problem numerycznego znajdowania takiego ekstremum. Jak każdy problem numeryczny ekstremum szukać będziemy zakładając pewną dokładność otrzymanego wyniku. | ||
| + | <source lang="python"> | ||
| − | |||
| − | |||
| − | |||
import time | import time | ||
import scipy.optimize as so | import scipy.optimize as so | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Wersja z 22:01, 7 cze 2015
Optymalizacja jednowymiarowa
Omawianie zagadnienia optymalizacji rozpocznijmy od prostego przykładu. Zdefiniujmy pewną funkcję i zobaczmy jak wygląda jej wykres.
import numpy as np
import pylab as py
licznikTestowej=0
def testowa(x):
global licznikTestowej
licznikTestowej+=1
return 1/x+np.exp(x)
xtest=np.arange(0.2,2,0.01)
ytest=[testowa(x) for x in xtest]
py.plot(xtest,ytest)
py.show()
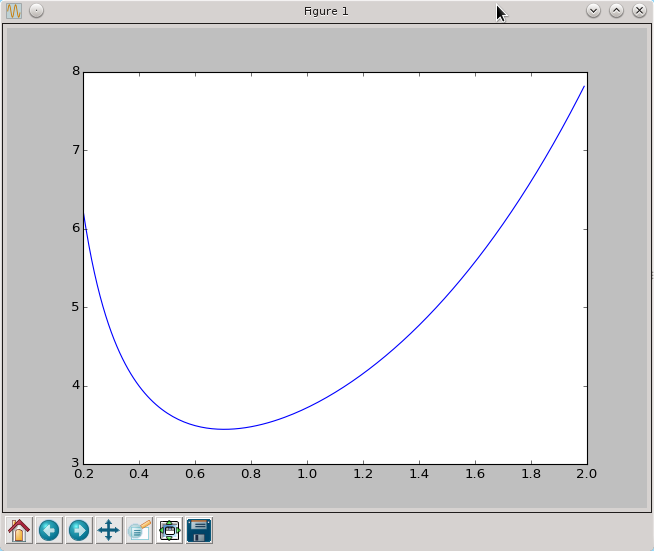 Na rozważanym przedziale [0.2,2] powyższa funkcją ma tylko jedno ekstremum lokalne. Taką funkcję nazywamy unimodalną. Zmienna licznikTestowej umożliwi nam zliczać wywołania funkcji testowej przez analizowane procedury.
Zagadnienie którym teraz będziemy się zajmować to problem numerycznego znajdowania takiego ekstremum. Jak każdy problem numeryczny ekstremum szukać będziemy zakładając pewną dokładność otrzymanego wyniku.
Na rozważanym przedziale [0.2,2] powyższa funkcją ma tylko jedno ekstremum lokalne. Taką funkcję nazywamy unimodalną. Zmienna licznikTestowej umożliwi nam zliczać wywołania funkcji testowej przez analizowane procedury.
Zagadnienie którym teraz będziemy się zajmować to problem numerycznego znajdowania takiego ekstremum. Jak każdy problem numeryczny ekstremum szukać będziemy zakładając pewną dokładność otrzymanego wyniku.
import time
import scipy.optimize as so
@stoper
def bruteForce(func,xmin,xmax,args=(),xtol=0.01):
xlist=np.arange(xmin,xmax,xtol)
ylist=[func(x,*args) for x in xlist]
#py.plot(xlist,ylist)
#py.show()
return xlist[ylist.index(max(ylist))]
#tutaj lepiej bez stopera!
def twoMidPointsR(func,xmin,xmax,args=(),xtol=0.01):
if xmax-xmin<xtol: return 0.5*(xmax+xmin)
xL=xmin+(xmax-xmin)/3.0
xR=xmax-(xmax-xmin)/3.0
fxL=func(xL,*args)
fxR=func(xR,*args)
if fxL>fxR:
return twoMidPointsR(func,xmin,xR,args,xtol)
else:
return twoMidPointsR(func,xL,xmax,args,xtol)
#szuka maximum funkcji
@stoper
def GoldenRatioRearch(func,xmin,xmax,args=(),xtol=0.01):
golden=0.5*(np.sqrt(5.0)-1.0)
xL=xmax-golden*(xmax-xmin)
xR=xmin+golden*(xmax-xmin)
fxL=func(xL,*args)
fxR=func(xR,*args)
while xmax-xmin>xtol:
if fxL<fxR:
xmin=xmin
xmax=xR
xR=xL
fxR=fxL
xL=xmax-golden*(xmax-xmin)
fxL=func(xL,*args)
else:
xmin=xL
xmax=xmax
xL=xR
fxL=fxR
xR=xmin+golden*(xmax-xmin)
fxR=func(xR,*args)
return 0.5*(xmax+xmin)
#test metody zlotego podzialu
#print GoldenRatioRearch(testowa,0,5,xtol=0.000001)
#print so.fmin(testowa,np.array([1]))[0]
#przypadek z jednym parametrem
def squares(a,func,xlist,ylist):
return sum([(func(xlist[i],*a)-ylist[i])**2 for i in range(len(xlist))])
#funkcja liniowa
def liniowa(x,a): return x*a
#funkcja kwadratowa
def kwadratowa(x,a,b=0): return a*x*x+b*x
#generujemy przykladowe xlist
xlist=np.arange(0,1,0.001)
#generujemy wartosci funkcji z szumem
ylist=[kwadratowa(x,1.23,-0.73)+0.000001*np.random.randn() for x in xlist]
#py.plot(xlist,ylist)
#py.show()
#lista przeszukiwanych wartosci parametru a
#alist=np.arange(0,10,0.01)
#wartosci squares dla tych parametrow
#squareslist=[squares(a,liniowa,xlist,ylist)for a in alist]
#zobaczmy wykres
#py.plot(alist,squareslist)
#py.show()
#najlepsze dopasowanie metoda brute force
#print bruteForce(squares,0,10,args=(liniowa,xlist,ylist),xtol=0.01)
#najlepsze dopasowanie metoda golden ration funkcji z 1 parametrem
#print GoldenRatioRearch(squares,0,10,args=(liniowa,xlist,ylist),xtol=0.01)
print so.fmin(squares,(1),args=(liniowa,xlist,ylist))
#najlepsze dopasowanie metoda symplexowa z dwoma parametrami
print so.fmin(squares,(1,0),args=(kwadratowa,xlist,ylist))
Optymalizacja wielowymiarowa
import numpy as np
import pylab as py
import scipy.optimize as so
#def squares(a,func,xlist,ylist):
# return sum([(func(xlist[i],*a)-ylist[i])**2 for i in range(len(xlist))])
#print so.fmin(squares,(1,0),args=(kwadratowa,xlist,ylist))
def rho_cauchy(x,loc,scale):
return (np.pi*scale*(1.0+(x-loc)**2/(scale**2)))**(-1.0)
def F_cauchy(x,loc,scale):
return 0.5+np.arctan((x-loc)*1.0/scale)/np.pi
#losujemy 10000 liczb z rozkladu Caychyego o loc=1.23 i scale=2.0
x=2*np.random.standard_cauchy(10000)+1.23
N=len(x)
#METODA 1 - Dopasowanie metoda najmniejszych kwadratow do histogramu
#tworzymy histogram
hist,bins= np.histogram(x,bins=np.linspace(-20,20,61))
#dlugosc przedzialu histogramowania
przedzial=bins[1]-bins[0]
#normalizujemy histogram aby moc go porownac z gestoscia
hist=hist*1.0/len(x)/przedzial
#liczymy wsp. srodkow przedzialow histogramowania
xhist=bins[:-1]+0.5*przedzial
#definiujemy sume kwadratow
def squares((loc,scale)):
return sum([(rho_cauchy(xhist[i],loc,scale)-hist[i])**2 for i in range(len(hist))])
#szukamy minimum funkcja fmin
fit1=tuple(so.fmin(squares,(0,1)))
print 'wynik metody1 to '+str(fit1)
#ogladamy wynik
py.plot(xhist,hist)
xtest=np.linspace(-20,20,1001)
ytest=[rho_cauchy(a,*fit1) for a in xtest]
py.plot(xtest,ytest)
py.show()
#METODA 2 - Metoda najwiekszej wiarygodnosci
#definiujemy -funkcje wiarygodnosci
def L((loc,scale)):
return -sum([np.log(rho_cauchy(a,loc,scale)) for a in x])
#szukamy minimum
fit2=tuple(so.fmin(L,(0,1)))
print 'wynik metody2 to '+str(fit2)
#METODA 3 - dopasowanie dystrybuant
xx=sorted(x)
yy=np.linspace(0,1,N)
#definiujemy funkcje KS bedaca maksimum z roznicy miedzy dystrybuanta empiryczna a teoretyczna
def KS((loc,scale)):
return max([abs(F_cauchy(xx[i],loc,scale)-yy[i]) for i in xrange(N)])
#szukamy minimum
fit3=tuple(so.fmin(KS,(0,1)))
print 'wynik metody3 to '+str(fit3)
#ogladamy wynik
cut=100
py.plot(xx[cut:-cut],yy[cut:-cut])
xtest=np.linspace(-20,20,1001)
ytest=[F_cauchy(x,*fit3) for x in xtest]
py.plot(xtest,ytest)
py.show()
Zadanie
Napisz data container...
import numpy as np
import pylab as py
import time
import scipy.optimize as so
class funkcja(object):
def __init__(self,*args):
self.args=args
def __str__(self):
return 'to jest funkcja o nazwie '+self.__class__.__name__+' i argumentach '+str(self.args)
class liniowa(funkcja):
def __call__(self,x):
return self.args[0]*x*x+self.args[1]
class DataContainer(object):
def __init__(self,x,y):
self.x=np.array(x)
self.y=np.array(y)
self.n=len(x)
def __str__(self):
return '''to jest Data Container z danymi:
x[:10]:'''+str(self.x[:10])+'''
y[:10]:'''+str(self.y[:10])
def fit(self,funkcja):
parametry_poczatkowe=funkcja.args
def squares(parametry):
funkcja.__init__(*tuple(parametry))
return sum((map(funkcja,self.x)-self.y)**2)
parametry_dopasowane=so.fmin(squares,parametry_poczatkowe)
funkcja.__init__(*tuple(parametry_dopasowane))
return funkcja
#generujemy przykladowe xlist
xlist=np.arange(0,1,0.001)
#generujemy wartosci funkcji z szumem
f=liniowa(1.23,-0.73)
ylist=[f(x)+0.05*np.random.randn() for x in xlist]
d=DataContainer(xlist,ylist)
f=liniowa(1,2)
f=d.fit(f)
py.plot(d.x,d.y)
py.plot(d.x,map(f,d.x))
py.show()