Obrazowanie:Obrazowanie Medyczne/Podstawowe Parametry Obrazów: Różnice pomiędzy wersjami
| (Nie pokazano 3 pośrednich wersji utworzonych przez tego samego użytkownika) | |||
| Linia 47: | Linia 47: | ||
===Dwuwymiarowa Transformata Fouriera=== | ===Dwuwymiarowa Transformata Fouriera=== | ||
Występujące w przyrodzie sygnały niejednokrotnie charakteryzują się wysokim stopniem złożoności, który utrudnia, a czasami wręcz uniemożliwia badanie ich właściwości. Na rysunkach <xr id="fig:linie_x_ft"> %i</xr> - <xr id="fig:linie_xy_ft"> %i</xr> zaprezentowano obrazy o bardzo prostej strukturze. Przykład obrazu o znacznym stopniu złożoności zaprezentowano na rysunku <xr id="fig:mandril">rys. %i</xr>. Wzrokowa analiza właściwości tego obrazu jest w zasadzie niemożliwa. Jedną z metod ułatwiających analizę skomplikowanego sygnału, zarówno jedno- jak i dwuwymiarowego, jest dobór odpowiedniej dla niego reprezentacji. Większość spośród stosowanych powszechnie typów reprezentacji ciągłych ma postać tzw. przekształcenia całkowego (inne określenie transformata całkowa). Najczęściej stosowaną transformatą w analizie sygnałów jednowymiarowych jest Transformata Fouriera, za pomocą której analizowany sygnał może być przedstawiony jako suma funkcji harmonicznych. Jest to o tyle istotne, iż funkcje te są niezmiennikami [[STAT:Systemy_liniowe_niezmiennicze_w_czasie_%28LTI%29|systemów LTI (ang. Linear Time-Invariant)]], pełniących niezwykle ważna rolę w przetwarzaniu sygnałów. Układy LTI występują również w systemach obrazowania medycznego, co będzie jeszcze omówione w dalszej części materiałów. Pary Transformat Fouriera dla przypadków jedno- i dwuwymiarowych, zarówno ciągłych jak i dyskretnych wyrażają poniższe wzory. | Występujące w przyrodzie sygnały niejednokrotnie charakteryzują się wysokim stopniem złożoności, który utrudnia, a czasami wręcz uniemożliwia badanie ich właściwości. Na rysunkach <xr id="fig:linie_x_ft"> %i</xr> - <xr id="fig:linie_xy_ft"> %i</xr> zaprezentowano obrazy o bardzo prostej strukturze. Przykład obrazu o znacznym stopniu złożoności zaprezentowano na rysunku <xr id="fig:mandril">rys. %i</xr>. Wzrokowa analiza właściwości tego obrazu jest w zasadzie niemożliwa. Jedną z metod ułatwiających analizę skomplikowanego sygnału, zarówno jedno- jak i dwuwymiarowego, jest dobór odpowiedniej dla niego reprezentacji. Większość spośród stosowanych powszechnie typów reprezentacji ciągłych ma postać tzw. przekształcenia całkowego (inne określenie transformata całkowa). Najczęściej stosowaną transformatą w analizie sygnałów jednowymiarowych jest Transformata Fouriera, za pomocą której analizowany sygnał może być przedstawiony jako suma funkcji harmonicznych. Jest to o tyle istotne, iż funkcje te są niezmiennikami [[STAT:Systemy_liniowe_niezmiennicze_w_czasie_%28LTI%29|systemów LTI (ang. Linear Time-Invariant)]], pełniących niezwykle ważna rolę w przetwarzaniu sygnałów. Układy LTI występują również w systemach obrazowania medycznego, co będzie jeszcze omówione w dalszej części materiałów. Pary Transformat Fouriera dla przypadków jedno- i dwuwymiarowych, zarówno ciągłych jak i dyskretnych wyrażają poniższe wzory. | ||
| − | Para jednowymiarowych Transformat Fouriera dla sygnału ciągłego <math>x(t)</math> | + | Para jednowymiarowych Transformat Fouriera dla sygnału ciągłego <math>x(t)</math>: |
| − | <equation> | + | <equation id="3"> |
<math> | <math> | ||
\begin{matrix} | \begin{matrix} | ||
| Linia 64: | Linia 64: | ||
Para jednowymiarowych dyskretnych Transformat Fouriera dla sygnału dyskretnego: | Para jednowymiarowych dyskretnych Transformat Fouriera dla sygnału dyskretnego: | ||
| − | <equation> | + | <equation id="4"> |
<math> | <math> | ||
\begin{array}{l} | \begin{array}{l} | ||
| Linia 76: | Linia 76: | ||
<math> N</math> — liczba dyskretnych punktów w sygnale. | <math> N</math> — liczba dyskretnych punktów w sygnale. | ||
| − | Para Transformat Fouriera funkcji ciągłej dwóch zmiennych <math>g(x,y)</math> | + | Para Transformat Fouriera funkcji ciągłej dwóch zmiennych <math>g(x,y)</math>: |
| − | <equation> | + | <equation id="5"> |
<math> | <math> | ||
\begin{array}{l} | \begin{array}{l} | ||
| Linia 93: | Linia 93: | ||
Para Dyskretnych Transformat Fouriera funkcji <math>g(k,l)</math> dwóch zmiennych dyskretnych <math>k</math> i <math>l</math>. | Para Dyskretnych Transformat Fouriera funkcji <math>g(k,l)</math> dwóch zmiennych dyskretnych <math>k</math> i <math>l</math>. | ||
| − | <equation> | + | <equation id="6"> |
<math> | <math> | ||
\begin{array}{l} | \begin{array}{l} | ||
| Linia 104: | Linia 104: | ||
gdzie:<br> | gdzie:<br> | ||
<math>M, N</math> — liczba dyskretnych punktów (liczba wierszy i kolumn w obrazie), | <math>M, N</math> — liczba dyskretnych punktów (liczba wierszy i kolumn w obrazie), | ||
| − | <equation> | + | <equation id="7"> |
<math> | <math> | ||
\begin{matrix} | \begin{matrix} | ||
| Linia 120: | Linia 120: | ||
Dotychczas pojecie sygnału kojarzyliśmy głównie z przebiegami pewnych wielkości fizycznych w czasie (np. sygnał EEG jest zapisem czynności elektrycznej mózgu). Termin sygnał można także stosować do obrazu. W tym przypadku sygnał jest reprezentacją pewnej mierzalnej cechy obiektu w przestrzeni (na <xr id="fig:linie_x_ft">rys. %i</xr> - <xr id="fig:linie_xy_ft">rys. %i</xr> cechą tą jest rozkład jasności obiektu). Jak pamiętamy z kursu [[STAT:Analiza_sygnałów|"Analiza Sygnałów"]], rzeczywiste układy pomiarowe, które realizują przetwarzanie sygnałów nazywamy systemem. System modelowany jest jako ''czarna skrzynka'', generująca odpowiedni sygnał wyjściowy w odpowiedzi na stan wejściowy. Szczególną klasę systemów przetwarzających sygnały, tworzą tzw. Układy Liniowe Niezmiennicze w Czasie (ang. ''Linear, Time Invariant Systems'', LTI). Oznaczmy przez <math>T\left\{\cdot\right\}</math> operacje wykonywane na sygnałach wejściowych ''x(t)'' oraz ''y(t)'', wtedy układ LTI charakteryzuje się następującymi własnościami: | Dotychczas pojecie sygnału kojarzyliśmy głównie z przebiegami pewnych wielkości fizycznych w czasie (np. sygnał EEG jest zapisem czynności elektrycznej mózgu). Termin sygnał można także stosować do obrazu. W tym przypadku sygnał jest reprezentacją pewnej mierzalnej cechy obiektu w przestrzeni (na <xr id="fig:linie_x_ft">rys. %i</xr> - <xr id="fig:linie_xy_ft">rys. %i</xr> cechą tą jest rozkład jasności obiektu). Jak pamiętamy z kursu [[STAT:Analiza_sygnałów|"Analiza Sygnałów"]], rzeczywiste układy pomiarowe, które realizują przetwarzanie sygnałów nazywamy systemem. System modelowany jest jako ''czarna skrzynka'', generująca odpowiedni sygnał wyjściowy w odpowiedzi na stan wejściowy. Szczególną klasę systemów przetwarzających sygnały, tworzą tzw. Układy Liniowe Niezmiennicze w Czasie (ang. ''Linear, Time Invariant Systems'', LTI). Oznaczmy przez <math>T\left\{\cdot\right\}</math> operacje wykonywane na sygnałach wejściowych ''x(t)'' oraz ''y(t)'', wtedy układ LTI charakteryzuje się następującymi własnościami: | ||
<ol><li>Liniowość. | <ol><li>Liniowość. | ||
| − | <equation> | + | <equation id="8"> |
<math>T\left\{x(t)+y(t)\right\}=T\left\{x(t)\right\}+T\left\{y(t)\right\}</math> | <math>T\left\{x(t)+y(t)\right\}=T\left\{x(t)\right\}+T\left\{y(t)\right\}</math> | ||
</equation> | </equation> | ||
| − | <equation> | + | <equation id="9"> |
<math>T\left\{ax(t)\right\}=aT\left\{x(t)\right\}</math> | <math>T\left\{ax(t)\right\}=aT\left\{x(t)\right\}</math> | ||
</equation> | </equation> | ||
<li> Niezmienniczość w czasie. | <li> Niezmienniczość w czasie. | ||
| − | <equation> | + | <equation id="10"> |
<math>T\left\{x(t+\tau)\right\}=T\left\{x(t)\right\}</math> | <math>T\left\{x(t+\tau)\right\}=T\left\{x(t)\right\}</math> | ||
</equation> | </equation> | ||
| Linia 133: | Linia 133: | ||
Przykładem układów LTI są filtry typu ''IIR'' oraz ''FIR''. Filtry te, jako układu LTI zmieniają amplitudę oraz poszczególnych składowych częstościowych sygnału. Nie mogą natomiast wytworzyć w sygnale składowych o nowych częstościach, co jest charakterystyczną cechą układów nielinowych. Operację przetwarzania sygnału przez układ LTI zapisujemy przy pomocy splotu. Niech ''x(t)'' będzie sygnałem na wejściu układu LTI, ''y(t)'' sygnałem na jego wyjściu, zaś ''h(t)'' odpowiedzią systemu LTI na impuls jednostkowy, wtedy zachodzi następująca relacja: | Przykładem układów LTI są filtry typu ''IIR'' oraz ''FIR''. Filtry te, jako układu LTI zmieniają amplitudę oraz poszczególnych składowych częstościowych sygnału. Nie mogą natomiast wytworzyć w sygnale składowych o nowych częstościach, co jest charakterystyczną cechą układów nielinowych. Operację przetwarzania sygnału przez układ LTI zapisujemy przy pomocy splotu. Niech ''x(t)'' będzie sygnałem na wejściu układu LTI, ''y(t)'' sygnałem na jego wyjściu, zaś ''h(t)'' odpowiedzią systemu LTI na impuls jednostkowy, wtedy zachodzi następująca relacja: | ||
| − | <equation> | + | <equation id="11"> |
<math>y(t)=\int\limits_{-\infty}^\infty x(\tau)h(t - \tau) d\tau = x(t)\ast h(t)</math> | <math>y(t)=\int\limits_{-\infty}^\infty x(\tau)h(t - \tau) d\tau = x(t)\ast h(t)</math> | ||
</equation> | </equation> | ||
| Linia 140: | Linia 140: | ||
Pojęcie układów LTI można rozszerzyć również na sygnały dwuwymiarowe, czyli np. obrazy. Niech ''g(x,y,)'' oraz ''v(x,y)'' będą dwoma obrazami na wejściu pewnego systemu, realizującego operację <math>T\left\{\cdot\right\}</math>. System nazwiemy liniowym, jeśli spełni następujące warunki: | Pojęcie układów LTI można rozszerzyć również na sygnały dwuwymiarowe, czyli np. obrazy. Niech ''g(x,y,)'' oraz ''v(x,y)'' będą dwoma obrazami na wejściu pewnego systemu, realizującego operację <math>T\left\{\cdot\right\}</math>. System nazwiemy liniowym, jeśli spełni następujące warunki: | ||
<ol><li>Liniowość. | <ol><li>Liniowość. | ||
| − | <equation> | + | <equation id="12"> |
<math>T\left\{g(x,y)+v(x,y)\right\}=T\left\{g(x,y)\right\}+T\left\{v(x,y)\right\}</math> | <math>T\left\{g(x,y)+v(x,y)\right\}=T\left\{g(x,y)\right\}+T\left\{v(x,y)\right\}</math> | ||
</equation> | </equation> | ||
| − | <equation> | + | <equation id="13"> |
<math>T\left\{ag(x,y)\right\}=aT\left\{g(x,y)\right\}</math> | <math>T\left\{ag(x,y)\right\}=aT\left\{g(x,y)\right\}</math> | ||
</equation> | </equation> | ||
<li> Niezmienniczość w czasie. | <li> Niezmienniczość w czasie. | ||
| − | <equation> | + | <equation id="14"> |
<math>T\left\{g(x,y,t+\tau)\right\}=T\left\{g(x,y,t)\right\}</math> | <math>T\left\{g(x,y,t+\tau)\right\}=T\left\{g(x,y,t)\right\}</math> | ||
</equation> | </equation> | ||
</ol> | </ol> | ||
Podobnie jak i w przypadku sygnałów jednowymiarowych, przykładem układów LTI w analizie obrazów są filtry cyfrowe. Własności filtrujące posiadają również znane z kursów fizyki soczewki, które działają jak filtry dolnoprzepustowe — usuwają z padającego na nie obrazu składowe o wysokich częstościach, przez co obraz po przejściu przez soczewkę staje się rozmyty. Wiele elementów aparatury stosowanej w obrazowaniu medycznym może być również traktowana jako układy LTI co znacznie ułatwia analizę ich działania. Relację pomiędzy obrazem na wejściu i wyjściu układu LTI można opisać za pomocą dwuwymiarowego splotu. Niech ''g(x,y)'' będzie obrazem wejściowym, ''v(x,y)'' obrazem na wyjściu systemu LTI, zaś i ''h(x,y)'' odpowiedzią układu LTI na punktowe źródło światła, wtedy: | Podobnie jak i w przypadku sygnałów jednowymiarowych, przykładem układów LTI w analizie obrazów są filtry cyfrowe. Własności filtrujące posiadają również znane z kursów fizyki soczewki, które działają jak filtry dolnoprzepustowe — usuwają z padającego na nie obrazu składowe o wysokich częstościach, przez co obraz po przejściu przez soczewkę staje się rozmyty. Wiele elementów aparatury stosowanej w obrazowaniu medycznym może być również traktowana jako układy LTI co znacznie ułatwia analizę ich działania. Relację pomiędzy obrazem na wejściu i wyjściu układu LTI można opisać za pomocą dwuwymiarowego splotu. Niech ''g(x,y)'' będzie obrazem wejściowym, ''v(x,y)'' obrazem na wyjściu systemu LTI, zaś i ''h(x,y)'' odpowiedzią układu LTI na punktowe źródło światła, wtedy: | ||
| − | <equation> | + | <equation id="15"> |
<math>v(x,y)=\int\limits_{-\infty}^\infty\int\limits_{-\infty}^\infty g(\tau_x,\tau_y)h(x - \tau_x,y-\tau_y)d\tau_xd\tau_y</math> | <math>v(x,y)=\int\limits_{-\infty}^\infty\int\limits_{-\infty}^\infty g(\tau_x,\tau_y)h(x - \tau_x,y-\tau_y)d\tau_xd\tau_y</math> | ||
</equation> | </equation> | ||
Operację splotu w dziedzinie częstości przestrzennych można zapisać w następujący sposób: | Operację splotu w dziedzinie częstości przestrzennych można zapisać w następujący sposób: | ||
| − | <equation> | + | <equation id="16"> |
<math>V(u,v)=G(u,v)\cdot H(u,v)</math> | <math>V(u,v)=G(u,v)\cdot H(u,v)</math> | ||
</equation> | </equation> | ||
| Linia 193: | Linia 193: | ||
:<math>I_B</math> — minimalna intensywność cechy fizycznej (np. natężenia światła) w interesującym nas obszarze przestrzeni lub obrazu. | :<math>I_B</math> — minimalna intensywność cechy fizycznej (np. natężenia światła) w interesującym nas obszarze przestrzeni lub obrazu. | ||
* Kontrast lokalny | * Kontrast lokalny | ||
| − | <equation> | + | <equation id="eq:kontrast_lokalny"> |
<math>C = \frac{I_A - I_B}{I_B}</math> | <math>C = \frac{I_A - I_B}{I_B}</math> | ||
</equation> | </equation> | ||
| Linia 200: | Linia 200: | ||
:<math>I_B</math> — intensywność cechy fizycznej (np. natężenia światła) otoczenia (tła) interesującego nas obiektu rzeczywistego lub jego odwzorowania na obrazie. | :<math>I_B</math> — intensywność cechy fizycznej (np. natężenia światła) otoczenia (tła) interesującego nas obiektu rzeczywistego lub jego odwzorowania na obrazie. | ||
* Stosunek Kontrastu do Szumu (ang. ''Contrast To Noise Ratio'', CNR). | * Stosunek Kontrastu do Szumu (ang. ''Contrast To Noise Ratio'', CNR). | ||
| − | <equation> | + | <equation id="eq:kontrast_snr"> |
<math>C = \frac{I_A - I_B}{\sigma}</math> | <math>C = \frac{I_A - I_B}{\sigma}</math> | ||
</equation> | </equation> | ||
| Linia 210: | Linia 210: | ||
W przypadku <xr id="fig:rozdzielczosc_kontrast">rys. %i</xr>.B obiekt składa się z trzech źródeł punktowych o kontraście lokalnym dążącym do nieskończoności. W wyniku rozmycia wprowadzonego przez urządzenie diagnostyczne, obrazy poszczególnych źródeł punktowych nakładają się na siebie. Natężenie światła tła na obrazie jest niezerowe, w związku z czym lokalny kontrast <math>C = \frac{I'_1 - I'_0}{I'_0}</math> osiąga wartość skończoną. <br> | W przypadku <xr id="fig:rozdzielczosc_kontrast">rys. %i</xr>.B obiekt składa się z trzech źródeł punktowych o kontraście lokalnym dążącym do nieskończoności. W wyniku rozmycia wprowadzonego przez urządzenie diagnostyczne, obrazy poszczególnych źródeł punktowych nakładają się na siebie. Natężenie światła tła na obrazie jest niezerowe, w związku z czym lokalny kontrast <math>C = \frac{I'_1 - I'_0}{I'_0}</math> osiąga wartość skończoną. <br> | ||
Systemy obrazujące powinny jak najwierniej odwzorowywać kontrast rzeczywistych obiektów. Na skutek niedoskonałości poszczególnych elementów układu obrazującego kontrast własny obiektu jest zniekształcony na obrazie (zwykle kontrast ulega zmniejszeniu). Przykładowo, standardowe soczewki działają jak filtry dolnoprzepustowe. Usuniecie z obrazu wysokich częstości przestrzennych, które odpowiedzialne są za odtwarzanie szczegółów obiektu, powoduje rozmycie jego krawędzi co jak wiemy (patrz <xr id="fig:kontrast">rys. %i</xr>) skutkuje w obniżeniu kontrastu. Funkcją, za pomocą której opisuje się wpływ elementu układu obrazującego na kontrast jest "Funkcja Przenoszenia Kontrastu"(ang. ''Contrast Transfer Function'', CTF). CTF to stosunek kontrastu na wyjściu układu obrazującego do kontrastu na wejściu tego układu, obliczany dla zadanej linii na jednostkę długości. | Systemy obrazujące powinny jak najwierniej odwzorowywać kontrast rzeczywistych obiektów. Na skutek niedoskonałości poszczególnych elementów układu obrazującego kontrast własny obiektu jest zniekształcony na obrazie (zwykle kontrast ulega zmniejszeniu). Przykładowo, standardowe soczewki działają jak filtry dolnoprzepustowe. Usuniecie z obrazu wysokich częstości przestrzennych, które odpowiedzialne są za odtwarzanie szczegółów obiektu, powoduje rozmycie jego krawędzi co jak wiemy (patrz <xr id="fig:kontrast">rys. %i</xr>) skutkuje w obniżeniu kontrastu. Funkcją, za pomocą której opisuje się wpływ elementu układu obrazującego na kontrast jest "Funkcja Przenoszenia Kontrastu"(ang. ''Contrast Transfer Function'', CTF). CTF to stosunek kontrastu na wyjściu układu obrazującego do kontrastu na wejściu tego układu, obliczany dla zadanej linii na jednostkę długości. | ||
| − | <equation> | + | <equation id="eq:CTF"> |
<math>CTF = \frac{C_{wy}\left(\frac{linie}{mm}\right)}{C_{wej}\left(\frac{linie}{mm}\right)}\times100%</math> | <math>CTF = \frac{C_{wy}\left(\frac{linie}{mm}\right)}{C_{wej}\left(\frac{linie}{mm}\right)}\times100%</math> | ||
</equation> | </equation> | ||
| Linia 236: | Linia 236: | ||
<br> | <br> | ||
W celu dogodniejszego opisu właściwości urządzenia obrazującego została wprowadzona tzw. Funkcja Przenoszenia Modulacji (ang. ''Modulation Transfer Function'', MTF). Omówienie tej funkcji zaczniemy od przypomnienia pojęcia głębokości modulacji. Załóżmy, iż zmiany jasności pewnego obiektu zachodzą wzdłuż jednego z jego boków z częstością ''u''. Amplituda zmian jasności, wokół pewnego stałego poziomu ''A'', wynosi ''B''. Zmiany jasności obiektu, które wyraża następujący wzór: | W celu dogodniejszego opisu właściwości urządzenia obrazującego została wprowadzona tzw. Funkcja Przenoszenia Modulacji (ang. ''Modulation Transfer Function'', MTF). Omówienie tej funkcji zaczniemy od przypomnienia pojęcia głębokości modulacji. Załóżmy, iż zmiany jasności pewnego obiektu zachodzą wzdłuż jednego z jego boków z częstością ''u''. Amplituda zmian jasności, wokół pewnego stałego poziomu ''A'', wynosi ''B''. Zmiany jasności obiektu, które wyraża następujący wzór: | ||
| − | <equation><math> | + | <equation id="17"><math> |
f(x,y) = A + B\sin(2\pi ux), | f(x,y) = A + B\sin(2\pi ux), | ||
</math></equation> | </math></equation> | ||
zaprezentowano na rys <xr id="fig:modulation_depth">rys. %i</xr>. | zaprezentowano na rys <xr id="fig:modulation_depth">rys. %i</xr>. | ||
Współczynnik głębokości modulacji to wielkość, która określa zmiany pewnego parametru względem pewnej stałej wartości. Jak widzimy na rys <xr id="fig:modulation_depth">rys. %i</xr> zmiany jasności obiektu osiągają amplitudę ''B'' względem pewnego poziomu jasności ''A''. W takim przypadku współczynnik głębokości modulacji określa poniższy wzór: | Współczynnik głębokości modulacji to wielkość, która określa zmiany pewnego parametru względem pewnej stałej wartości. Jak widzimy na rys <xr id="fig:modulation_depth">rys. %i</xr> zmiany jasności obiektu osiągają amplitudę ''B'' względem pewnego poziomu jasności ''A''. W takim przypadku współczynnik głębokości modulacji określa poniższy wzór: | ||
| − | <equation><math> | + | <equation id="18"><math> |
m = \frac{B}{A}. | m = \frac{B}{A}. | ||
</math></equation> | </math></equation> | ||
Wykonajmy teraz obraz obiektu za pomocą układu LTI. Przypominamy, że układ LTI może zmieniać amplitudę i fazę poszczególnych częstości przestrzennych. W związku z tym, na wyjściu układu otrzymamy obraz <math>g(x,y)</math>, którego zmiany jasności będą opisane wzorem: | Wykonajmy teraz obraz obiektu za pomocą układu LTI. Przypominamy, że układ LTI może zmieniać amplitudę i fazę poszczególnych częstości przestrzennych. W związku z tym, na wyjściu układu otrzymamy obraz <math>g(x,y)</math>, którego zmiany jasności będą opisane wzorem: | ||
| − | <equation><math> | + | <equation id="19"><math> |
g(x,y) = C + D\sin(2\pi ux), | g(x,y) = C + D\sin(2\pi ux), | ||
</math></equation> | </math></equation> | ||
natomiast współczynnik modulacji wyniesie: | natomiast współczynnik modulacji wyniesie: | ||
| − | <equation><math> | + | <equation id="20"><math> |
m = \frac{D}{C}. | m = \frac{D}{C}. | ||
</math></equation> | </math></equation> | ||
Możemy zbadać teraz, jak układ LTI przeniósł współczynnik głębokości modulacji w następujący sposób: | Możemy zbadać teraz, jak układ LTI przeniósł współczynnik głębokości modulacji w następujący sposób: | ||
| − | <equation><math> | + | <equation id="21"><math> |
H = \frac{\frac{D}{C}}{\frac{B}{A}} = \frac{D\cdot A}{C\cdot B}. | H = \frac{\frac{D}{C}}{\frac{B}{A}} = \frac{D\cdot A}{C\cdot B}. | ||
</math></equation> | </math></equation> | ||
| Linia 261: | Linia 261: | ||
Zmiany w jasności, czy też innych cechach rzeczywistych obiektów są jednak znacznie bardziej skomplikowane niż powyższy przykład. | Zmiany w jasności, czy też innych cechach rzeczywistych obiektów są jednak znacznie bardziej skomplikowane niż powyższy przykład. | ||
Jednakże, zarówno rzeczywiste obiekty, jak też ich obrazy, możemy przedstawić jako szereg harmonicznych oscylacji przestrzennych. Załóżmy, iż obiekt, zmiany jasności opisuje funkcja <math>f(x,y)</math> oraz jego obraz <math>g(x,y)</math> rozłożyliśmy na Szereg Fouriera: | Jednakże, zarówno rzeczywiste obiekty, jak też ich obrazy, możemy przedstawić jako szereg harmonicznych oscylacji przestrzennych. Załóżmy, iż obiekt, zmiany jasności opisuje funkcja <math>f(x,y)</math> oraz jego obraz <math>g(x,y)</math> rozłożyliśmy na Szereg Fouriera: | ||
| − | <equation> | + | <equation id="22"> |
<math> | <math> | ||
\begin{array}{l} | \begin{array}{l} | ||
| Linia 276: | Linia 276: | ||
Niech obiekt ''f(x,y)'' o widmie ''F(u,v)'' zostanie odwzorowany za pomocą układu LTI na obrazie <math>g(x,y)</math> o widmie <math>G(u,v)</math>. Układ LTI scharakteryzowany jest przy pomocy funkcji odpowiedzi impulsowej ''h(x,y)'' o widmie <math>H(u,v)</math>. Z własności układów LTI wiemy, iż pomiędzy stanem wejściowym (obrazowanym obiektem) a wyjściem (obrazem) istnieje następujący związek: | Niech obiekt ''f(x,y)'' o widmie ''F(u,v)'' zostanie odwzorowany za pomocą układu LTI na obrazie <math>g(x,y)</math> o widmie <math>G(u,v)</math>. Układ LTI scharakteryzowany jest przy pomocy funkcji odpowiedzi impulsowej ''h(x,y)'' o widmie <math>H(u,v)</math>. Z własności układów LTI wiemy, iż pomiędzy stanem wejściowym (obrazowanym obiektem) a wyjściem (obrazem) istnieje następujący związek: | ||
| − | <equation> | + | <equation id="23"> |
<math> G(u,v) = H(u,v)F(u,v)</math> | <math> G(u,v) = H(u,v)F(u,v)</math> | ||
</equation> | </equation> | ||
Przypominamy również, że moduł Transformaty Fouriera odpowiada amplitudzie danej składowej harmonicznej, w związku z czym możemy zapisać: | Przypominamy również, że moduł Transformaty Fouriera odpowiada amplitudzie danej składowej harmonicznej, w związku z czym możemy zapisać: | ||
| − | <equation> | + | <equation id="24"> |
<math> | <math> | ||
\begin{array}{l} | \begin{array}{l} | ||
| Linia 296: | Linia 296: | ||
</equation> | </equation> | ||
Korzystając z powyższych zależności możemy zapisać: | Korzystając z powyższych zależności możemy zapisać: | ||
| − | <equation> | + | <equation id="25"> |
<math> g(x,y) = H(0,0)A + \sum_i\sum_jH(u_i,v_j)B_{ij}\sin(2\pi u_ix+2\pi v_jy) </math> | <math> g(x,y) = H(0,0)A + \sum_i\sum_jH(u_i,v_j)B_{ij}\sin(2\pi u_ix+2\pi v_jy) </math> | ||
</equation> | </equation> | ||
W przypadku obiektu złożonego z wielu składowych harmonicznych, głębokość modulacji może być inna dla każdej częstości przestrzennej: | W przypadku obiektu złożonego z wielu składowych harmonicznych, głębokość modulacji może być inna dla każdej częstości przestrzennej: | ||
| − | <equation> | + | <equation id="26"> |
<math>m_{u_i,v_j} = \frac{B_{ij}}{A}</math> | <math>m_{u_i,v_j} = \frac{B_{ij}}{A}</math> | ||
</equation> | </equation> | ||
Zauważmy teraz, iż głębokość modulacji <math>m^g_{u_i,v_j}</math> obrazu ''g(x,y)'' można wyrazić w następujący sposób: | Zauważmy teraz, iż głębokość modulacji <math>m^g_{u_i,v_j}</math> obrazu ''g(x,y)'' można wyrazić w następujący sposób: | ||
| − | <equation> | + | <equation id="27"> |
<math> m^g_{u_i,v_j} = \frac{|H(u_i,v_j)|B_{ij}}{|H(0,0)|A}</math> | <math> m^g_{u_i,v_j} = \frac{|H(u_i,v_j)|B_{ij}}{|H(0,0)|A}</math> | ||
</equation> | </equation> | ||
Zbadajmy teraz, jak głębokość modulacji <math>m^f_{u_i,v_j}</math> rzeczywistego obiektu została odwzorowana na obrazie. Głębokość modulacji obrazu oznaczmy <math>m^g_{u_i,v_j}</math> | Zbadajmy teraz, jak głębokość modulacji <math>m^f_{u_i,v_j}</math> rzeczywistego obiektu została odwzorowana na obrazie. Głębokość modulacji obrazu oznaczmy <math>m^g_{u_i,v_j}</math> | ||
| − | <equation> | + | <equation id="28"> |
<math>\frac{m^g_{u_i,v_j}}{m^f_{u_i,v_j}} = \frac{|H(u_i,v_j)|B_{ij}}{|H(0,0)|A}\frac{A}{B_{ij}} = \frac{|H(u_i,v_j)|}{|H(0,0)|}</math> | <math>\frac{m^g_{u_i,v_j}}{m^f_{u_i,v_j}} = \frac{|H(u_i,v_j)|B_{ij}}{|H(0,0)|A}\frac{A}{B_{ij}} = \frac{|H(u_i,v_j)|}{|H(0,0)|}</math> | ||
</equation> | </equation> | ||
Wielkość opisującą stosunek głębokości modulacji dla zadanych częstości przestrzennych w obrazie, do głębokości modulacji dla tych samych częstości przestrzennych w rzeczywistym obiekcie nazywamy Funkcją Przenoszenia Modulacji (MTF): | Wielkość opisującą stosunek głębokości modulacji dla zadanych częstości przestrzennych w obrazie, do głębokości modulacji dla tych samych częstości przestrzennych w rzeczywistym obiekcie nazywamy Funkcją Przenoszenia Modulacji (MTF): | ||
| − | <equation> | + | <equation id="29"> |
<math> MTF(u_i,v_j) = \frac{|H(u_i,v_j)|}{|H(0,0)|}</math> | <math> MTF(u_i,v_j) = \frac{|H(u_i,v_j)|}{|H(0,0)|}</math> | ||
</equation> | </equation> | ||
| Linia 321: | Linia 321: | ||
Linie x ft.png | Linie x ft.png | ||
Obiekt zaprezentowany na <xr id="fig:mtf_kontrast">rys. %i</xr> może zostać opisany za pomocą jednej funkcji harmonicznej biegnącej wzdłuż osi ''X'': | Obiekt zaprezentowany na <xr id="fig:mtf_kontrast">rys. %i</xr> może zostać opisany za pomocą jednej funkcji harmonicznej biegnącej wzdłuż osi ''X'': | ||
| − | <equation> | + | <equation id="30"> |
<math> | <math> | ||
f(x,y) = A_0 + B_0\sin(2\pi u_0 x) | f(x,y) = A_0 + B_0\sin(2\pi u_0 x) | ||
| Linia 328: | Linia 328: | ||
gdzie: <math>u_0=32\frac{\textrm{1}}{\textrm{m}}</math>. <br> | gdzie: <math>u_0=32\frac{\textrm{1}}{\textrm{m}}</math>. <br> | ||
Maksima funkcji harmonicznej tworzą pionowe jasne linie. Odległość pomiędzy tymi liniami <math>\Delta x</math> jest odwrotnością częstości przestrzennej funkcji harmonicznej <math>u_0</math>: | Maksima funkcji harmonicznej tworzą pionowe jasne linie. Odległość pomiędzy tymi liniami <math>\Delta x</math> jest odwrotnością częstości przestrzennej funkcji harmonicznej <math>u_0</math>: | ||
| − | <equation> | + | <equation id="31"> |
<math> \Delta x = \frac{1}{u_0}</math> | <math> \Delta x = \frac{1}{u_0}</math> | ||
</equation> | </equation> | ||
Obraz ''g(x,y)'' obiektu ''f(x,y)'' może być rozłożony na składowe harmoniczne w następujący sposób: | Obraz ''g(x,y)'' obiektu ''f(x,y)'' może być rozłożony na składowe harmoniczne w następujący sposób: | ||
| − | <equation> | + | <equation id="32"> |
<math> | <math> | ||
g(x,y) = C + D_0\sin(2\pi u_0 x) | g(x,y) = C + D_0\sin(2\pi u_0 x) | ||
| Linia 338: | Linia 338: | ||
</equation> | </equation> | ||
Związek pomiędzy składowymi harmonicznymi obrazu ''g(x,y)'' na wyjściu układu LTI, a składowymi harmonicznymi rzeczywistego obiektu ''f(x,y)'' na wejściu tego układu, wyraża poniższa zależność | Związek pomiędzy składowymi harmonicznymi obrazu ''g(x,y)'' na wyjściu układu LTI, a składowymi harmonicznymi rzeczywistego obiektu ''f(x,y)'' na wejściu tego układu, wyraża poniższa zależność | ||
| − | <equation> | + | <equation id="33"> |
<math> | <math> | ||
\begin{array}{l} | \begin{array}{l} | ||
| Linia 364: | Linia 364: | ||
<math> A_{\max}, A_{\min}</math> to odpowiednio maksymalna i minimalna amplituda zmian obserwowana w sygnale. <br> | <math> A_{\max}, A_{\min}</math> to odpowiednio maksymalna i minimalna amplituda zmian obserwowana w sygnale. <br> | ||
Obliczmy kontrast globalny obiektu opisanego wzorem (<xr id="eq:eq2"> %i</xr>): | Obliczmy kontrast globalny obiektu opisanego wzorem (<xr id="eq:eq2"> %i</xr>): | ||
| − | <equation><math>C = \frac{A + B - (A - B)}{A + B + (A - B)} = \frac{B}{A}</math></equation> | + | <equation id="34"><math>C = \frac{A + B - (A - B)}{A + B + (A - B)} = \frac{B}{A}</math></equation> |
Jak możemy zauważyć, uzyskany kontrast jest tożsamy z głębokością modulacji sygnału harmonicznego, który wynosi: | Jak możemy zauważyć, uzyskany kontrast jest tożsamy z głębokością modulacji sygnału harmonicznego, który wynosi: | ||
| − | <equation><math>m = \frac{B}{A}</math></equation> | + | <equation id="35"><math>m = \frac{B}{A}</math></equation> |
Modulacja sygnału jest wielkością, której przenoszenie przez układ LTI opisuje funkcja MTF. | Modulacja sygnału jest wielkością, której przenoszenie przez układ LTI opisuje funkcja MTF. | ||
Doszliśmy zatem do wniosku, iż funkcja MTF pośrednio opisuje przenoszenie kontrastu zawartego w sygnale przez układ LTI. | Doszliśmy zatem do wniosku, iż funkcja MTF pośrednio opisuje przenoszenie kontrastu zawartego w sygnale przez układ LTI. | ||
| Linia 375: | Linia 375: | ||
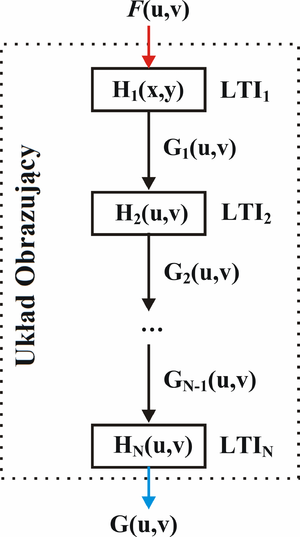
Układu wykorzystywane w obrazowaniu medycznych są zbudowane z bardzo wielu elementów (źródeł promieniowania, układów formujących wiązki promieniowania, detektorów, itd.), które mają wpływ na uzyskiwany obraz. Nawet w budowie zwykłego aparatu fotograficznego możemy wyróżnić kilka podzespołów, takich jak obiektyw oraz detektor promieniowania (film lub matrycę CCD). Obiektyw z kolei złożony jest najczęściej z przesłony i kilku soczewek, których działanie może być opisane w formalizmie systemów LTI. Czy znając funkcję MTF dla każdego z elementów układu obrazującego jesteśmy w stanie coś wywnioskować na temat jakości obrazu uzyskanego przez cały układ obrazujący? Okazuje się że tak. Załóżmy, że nasz system obrazujący składa się z ''N'' bloków (czarnych skrzynek), z których każda może być opisana jako układ LTI. Schemat takiego urządzenia zaprezentowano na <xr id="fig:lti_mtf">rys. %i</xr>. | Układu wykorzystywane w obrazowaniu medycznych są zbudowane z bardzo wielu elementów (źródeł promieniowania, układów formujących wiązki promieniowania, detektorów, itd.), które mają wpływ na uzyskiwany obraz. Nawet w budowie zwykłego aparatu fotograficznego możemy wyróżnić kilka podzespołów, takich jak obiektyw oraz detektor promieniowania (film lub matrycę CCD). Obiektyw z kolei złożony jest najczęściej z przesłony i kilku soczewek, których działanie może być opisane w formalizmie systemów LTI. Czy znając funkcję MTF dla każdego z elementów układu obrazującego jesteśmy w stanie coś wywnioskować na temat jakości obrazu uzyskanego przez cały układ obrazujący? Okazuje się że tak. Załóżmy, że nasz system obrazujący składa się z ''N'' bloków (czarnych skrzynek), z których każda może być opisana jako układ LTI. Schemat takiego urządzenia zaprezentowano na <xr id="fig:lti_mtf">rys. %i</xr>. | ||
Właściwości każdego z elementów układu obrazującego w dziedzinie częstości przestrzennych opisane są przy pomocy funkcji przejścia <math>H_i(u,v)</math>, gdzie ''u'',''v'' to częstości przestrzenne. Na wejściu układu obrazującego podawany jest sygnał o widmie <math>F(u,v)</math>. Trafia on jednocześnie na wejście pierwszego układu LTI. Na wyjściu pierwszego układu LTI sygnał będzie miał postać: | Właściwości każdego z elementów układu obrazującego w dziedzinie częstości przestrzennych opisane są przy pomocy funkcji przejścia <math>H_i(u,v)</math>, gdzie ''u'',''v'' to częstości przestrzenne. Na wejściu układu obrazującego podawany jest sygnał o widmie <math>F(u,v)</math>. Trafia on jednocześnie na wejście pierwszego układu LTI. Na wyjściu pierwszego układu LTI sygnał będzie miał postać: | ||
| − | <equation><math>G_1(u,v) = H_1(u,v)\cdot F(u,v)</math></equation> | + | <equation id="36"><math>G_1(u,v) = H_1(u,v)\cdot F(u,v)</math></equation> |
Sygnał wyjściowy z pierwszego układu LTI jest sygnałem wejściowym dla kolejnego układu. W związku z tym, na wyjściu drugiego układu LTI pojawi sygnał: | Sygnał wyjściowy z pierwszego układu LTI jest sygnałem wejściowym dla kolejnego układu. W związku z tym, na wyjściu drugiego układu LTI pojawi sygnał: | ||
| − | <equation><math>G_2(u,v) = H_2(u,v)\cdot G_1(u,v) = H_2(u,v)\cdot H_1(u,v)\cdot F(u,v)</math></equation> | + | <equation id="37"><math>G_2(u,v) = H_2(u,v)\cdot G_1(u,v) = H_2(u,v)\cdot H_1(u,v)\cdot F(u,v)</math></equation> |
Ostatecznie, po przejściu przez ''N'' układów LTI, na wyjściu układu obrazującego uzyskamy sygnał: | Ostatecznie, po przejściu przez ''N'' układów LTI, na wyjściu układu obrazującego uzyskamy sygnał: | ||
<equation id="eq:lti_mtf"><math>G(u,v) = H_2(u,v)\cdot G_1(u,v) = H_N(u,v)\cdot \ldots \cdot H_2(u,v)\cdot H_1(u,v)\cdot F(u,v)</math></equation> | <equation id="eq:lti_mtf"><math>G(u,v) = H_2(u,v)\cdot G_1(u,v) = H_N(u,v)\cdot \ldots \cdot H_2(u,v)\cdot H_1(u,v)\cdot F(u,v)</math></equation> | ||
Dla całego układu obrazującego możemy zatem zdefiniować następująca funkcję przejścia: | Dla całego układu obrazującego możemy zatem zdefiniować następująca funkcję przejścia: | ||
| − | <equation><math>H(u,v) = H_2(u,v)\cdot G_1(u,v) = H_N(u,v)\cdot \ldots \cdot H_2(u,v)\cdot H_1(u,v) </math></equation> | + | <equation id="38"><math>H(u,v) = H_2(u,v)\cdot G_1(u,v) = H_N(u,v)\cdot \ldots \cdot H_2(u,v)\cdot H_1(u,v) </math></equation> |
i wyznaczyć funkcję MTF tego układu: | i wyznaczyć funkcję MTF tego układu: | ||
| − | <equation><math>MTF(u,v) = \frac{|H(u,v)|}{H(0,0)} </math></equation> | + | <equation id="39"><math>MTF(u,v) = \frac{|H(u,v)|}{H(0,0)} </math></equation> |
Funkcję MTF można również wyznaczyć znając przebieg funkcji przenoszenia modulacji <math>MTF_i(u,v) = \frac{H_1(u,v)}{ H_1(0,0)}</math> każdego systemu LTI wchodzącego w skład układu obrazującego, co wynika ze wzoru (<xr id="eq:lti_mtf"> %i</xr>): | Funkcję MTF można również wyznaczyć znając przebieg funkcji przenoszenia modulacji <math>MTF_i(u,v) = \frac{H_1(u,v)}{ H_1(0,0)}</math> każdego systemu LTI wchodzącego w skład układu obrazującego, co wynika ze wzoru (<xr id="eq:lti_mtf"> %i</xr>): | ||
| − | <equation><math>MTF(u,v) = MTF_1(u,v)\cdot MTF_2(u,v)\cdot \ldots \cdot MTF_N(u,v)</math></equation> | + | <equation id="40"><math>MTF(u,v) = MTF_1(u,v)\cdot MTF_2(u,v)\cdot \ldots \cdot MTF_N(u,v)</math></equation> |
===Zalety Funkcji MTF=== | ===Zalety Funkcji MTF=== | ||
| Linia 397: | Linia 397: | ||
Przypominamy na początku, że działanie systemu obrazującego o własnościach układu LTI można opisać następującym wzorem: | Przypominamy na początku, że działanie systemu obrazującego o własnościach układu LTI można opisać następującym wzorem: | ||
| − | <equation> | + | <equation id="41"> |
<math>v(x,y)=\int\limits_{-\infty}^\infty\int\limits_{-\infty}^\infty g(\tau_x,\tau_y)h(x - \tau_x,y-\tau_y)d\tau_xd\tau_y</math> | <math>v(x,y)=\int\limits_{-\infty}^\infty\int\limits_{-\infty}^\infty g(\tau_x,\tau_y)h(x - \tau_x,y-\tau_y)d\tau_xd\tau_y</math> | ||
</equation> | </equation> | ||
| Linia 408: | Linia 408: | ||
</ul> | </ul> | ||
Funkcję <math>h(x,y)</math> nazywamy punktową funkcja rozproszenia (ang. ''Point Spread Function'',PSF). Transformatę Fouriera <math> OTF(u,v)</math> funkcji PSF: | Funkcję <math>h(x,y)</math> nazywamy punktową funkcja rozproszenia (ang. ''Point Spread Function'',PSF). Transformatę Fouriera <math> OTF(u,v)</math> funkcji PSF: | ||
| − | <equation><math> | + | <equation id="41"><math> |
OTF(u,v) = \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}h(x,y) e^{-2\pi i(ux + vy)}dxdy | OTF(u,v) = \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}h(x,y) e^{-2\pi i(ux + vy)}dxdy | ||
</math></equation> | </math></equation> | ||
| Linia 414: | Linia 414: | ||
nazywamy optyczną funkcją przenoszenia (ang. ''Optical Transfer Function'',OTF). Funkcję OTF tę można zapisać w następujący sposób: | nazywamy optyczną funkcją przenoszenia (ang. ''Optical Transfer Function'',OTF). Funkcję OTF tę można zapisać w następujący sposób: | ||
| − | <equation><math> | + | <equation id="42"><math> |
OTF(u,v) = |OTF|e^{-i\phi(u,v)} | OTF(u,v) = |OTF|e^{-i\phi(u,v)} | ||
</math></equation> | </math></equation> | ||
| Linia 421: | Linia 421: | ||
Moduł Transformaty Fouriera funkcji PSF, znormalizowany w ten sposób, aby | Moduł Transformaty Fouriera funkcji PSF, znormalizowany w ten sposób, aby | ||
<math>|OTF(0,0)| = 1</math> nazywamy funkcją przenoszenia modulacji: | <math>|OTF(0,0)| = 1</math> nazywamy funkcją przenoszenia modulacji: | ||
| − | <equation><math> | + | <equation id="43"><math> |
MTF(u,v) = \frac{|OTF(u,v)|}{|OTF(0,0)|} | MTF(u,v) = \frac{|OTF(u,v)|}{|OTF(0,0)|} | ||
</math></equation> | </math></equation> | ||
z kolei argument funkcji OTF nazywamy funkcją przenoszenia fazy (ang. ''Phase Transfer Function'',PTF): | z kolei argument funkcji OTF nazywamy funkcją przenoszenia fazy (ang. ''Phase Transfer Function'',PTF): | ||
| − | <equation><math> | + | <equation id="44"><math> |
PTF(u,v) = \arg(OTF(u,v)) | PTF(u,v) = \arg(OTF(u,v)) | ||
</math></equation> | </math></equation> | ||
| Linia 432: | Linia 432: | ||
Obrazem punktowego źródła światła, znajdującego się w nieskończonej odległości od kamery otworkowej jest krążek o średnicy ''d'' równej średnicy obiektywu (otworka) kamery i równomiernym rozkładzie natężenia światła ''A'', który możemy opisać następującym wzorem: | Obrazem punktowego źródła światła, znajdującego się w nieskończonej odległości od kamery otworkowej jest krążek o średnicy ''d'' równej średnicy obiektywu (otworka) kamery i równomiernym rozkładzie natężenia światła ''A'', który możemy opisać następującym wzorem: | ||
| − | <equation><math> | + | <equation id="45"><math> |
PSF(x,y) = \left\{\begin{array}{l} | PSF(x,y) = \left\{\begin{array}{l} | ||
A, \textrm{\ dla\ } \sqrt{x^2 + y^2} \leq d\\ | A, \textrm{\ dla\ } \sqrt{x^2 + y^2} \leq d\\ | ||
| Linia 443: | Linia 443: | ||
Transformata Fouriera funkcji PSF(x,y) wynosi: | Transformata Fouriera funkcji PSF(x,y) wynosi: | ||
| − | <equation><math> | + | <equation id="46"><math> |
OTF(u,v) = FFT(PSF(x,y)) = \frac{J_1(2\pi d\rho)}{ 2\pi d\rho } | OTF(u,v) = FFT(PSF(x,y)) = \frac{J_1(2\pi d\rho)}{ 2\pi d\rho } | ||
</math></equation> | </math></equation> | ||
| Linia 453: | Linia 453: | ||
</ul> | </ul> | ||
Funkcja przenoszenia modulacji – MTF, to moduł znormalizowanej funkcji OTF. Wartość funkcji OTF w punkcie <math>(0,0)</math> wynosi <math>\frac{1}{2}</math>, w związku z czym funkcja MTF jest równa: | Funkcja przenoszenia modulacji – MTF, to moduł znormalizowanej funkcji OTF. Wartość funkcji OTF w punkcie <math>(0,0)</math> wynosi <math>\frac{1}{2}</math>, w związku z czym funkcja MTF jest równa: | ||
| − | <equation><math> | + | <equation id="47"><math> |
MTF(u,v) = 2\cdot|OTF(u,v)| = 2\frac{J_1(2\pi d\rho)}{ 2\pi d\rho} | MTF(u,v) = 2\cdot|OTF(u,v)| = 2\frac{J_1(2\pi d\rho)}{ 2\pi d\rho} | ||
</math></equation> | </math></equation> | ||
| Linia 459: | Linia 459: | ||
Wykres funkcji OTF oraz MTF zaprezentowano na <xr id="bessel_2">rys. %i</xr>. | Wykres funkcji OTF oraz MTF zaprezentowano na <xr id="bessel_2">rys. %i</xr>. | ||
Funkcja MTF osiąga pierwsze miejsce zerowe dla argumentu równego | Funkcja MTF osiąga pierwsze miejsce zerowe dla argumentu równego | ||
| − | <equation><math> | + | <equation id="48"><math> |
\rho_g = \frac{0.61}{d} | \rho_g = \frac{0.61}{d} | ||
</math></equation> | </math></equation> | ||
Wielkość <math>\rho_g</math> to górna granica pasma częstości przestrzennych przenoszonych przez Kamerę Otworkową. | Wielkość <math>\rho_g</math> to górna granica pasma częstości przestrzennych przenoszonych przez Kamerę Otworkową. | ||
Aktualna wersja na dzień 19:51, 28 wrz 2015
Podstawowe Parametry Obrazów
Zanim omówimy podstawowe parametry obrazów uzyskiwanych w diagnostyce medycznej, spróbujemy określić pojęcie obrazu. Każdy z nas zapewne widział wielokrotnie zdjęcie fotograficzne. Jeszcze do niedawana zdjęcia takie było wykonywane przy pomocy aparatu fotograficznego wyposażonego w obiektyw i kliszę fotograficzną, która pełniła rolę detektora światła. Współczesne aparaty fotograficzne zamiast kliszy posiadają matrycę CCD (ang. Charge Coupled Device, CCD). Zarówno w przypadku analogowych, jak i cyfrowych aparatów, zdjęcie fotograficzne powstaje w efekcie naświetlania detektora przez wiązkę światła emitowanego lub odbijanego przez fotografowany obiekt. Zdolność do emisji lub odbijania światła jest pewną cechą obiektu. Możemy zatem stwierdzić, że obraz to odwzorowanie pewnej cechy obiektu przestrzeni trójwymiarowej na płaszczyznę. W przypadku obrazowania medycznego cechą obiektów może być:
- Liniowy współczynnik osłabienia promieniowania Rentgenowskiego (Radiografia Rentgenowska, Rentgenowska Tomografia Komputerowa).
- Rozkład radionuklidu promieniotwórczego (Obrazowanie Nuklearne).
- Gęstość protonów (MRI).
Komputerowe przetwarzanie obrazów jest możliwe tylko dla obrazów cyfrowych, to jest skwantowanych ([1]) i dyskretnych ([2]). Pojedynczy element obrazu cyfrowego nazywamy pikselem. Naturalnym sposobem matematycznej reprezentacji takiego obrazu jest dwuwymiarowa macierz. Każdy element macierzy odpowiada pojedynczemu pikselowi i zawiera liczbę określającą cechę obrazowanego obiektu. Jeśli obraz uzyskujemy za pomocą detektorów analogowych (np. błony fotograficznej), zawsze możemy go zamienić na postać cyfrową za pomocą przetworników analogowo – cyfrowych ([3]).
Obrazy uzyskiwane na potrzeby diagnostyki medycznej muszą charakteryzować się odpowiednią jakością. Do najważniejszych parametrów obrazu należą:
- rozdzielczość,
- kontrast.
Pojęcia te omówimy analizując działanie najstarszego i najprostszego urządzenia optycznego jakim jest Camera Obscura (patrz rys. 1).
Spis treści
- 1 Camera Obscura
- 2 Układy LTI w przetwarzaniu obrazów
- 3 O rozdzielczości raz jeszcze
- 4 Kontrast. Funkcja Przenoszenia Kontrastu.
- 5 Modulacja. Funkcja przenoszenia Modulacji.
- 5.1 Funkcja Przenoszenia Modulacji a rozdzielczość przestrzenna.
- 5.2 Funkcja Przenoszenia Modulacji a przenoszenie kontrastu.
- 5.3 Funkcja MTF złożonych układów obrazowania
- 5.4 Zalety Funkcji MTF
- 5.5 Wyznaczanie funkcji MTF na przykładzie Kamery Otworkowej
- 5.6 Przykład wyznaczenia funkcji MTF dla Kamery Otworkowej
Camera Obscura
Camera Obscura to urządzenie optyczne składające się z wyczernionego wewnątrz pudełka oraz małego otworu (pełniącego rolę obiektywu), który znajduje się w jednej ze ścian pudełka. Nazwa urządzenia w bezpośrednim tłumaczeniu z języka łacińskiego oznacza ciemną komnatę i jest nieprzypadkowa. Na przestrzeni dziejów, duże, ciemne pomieszczenia z otworem w okiennicach lub dachu służyły to uzyskiwania obrazów różnych obiektów, np. Johannes Kepler wykorzystywał do obserwacji plam słonecznych katedrę w Ratyzbonie, z wykonanym w jej dachu małym otworem. W języku angielskim Camera Obscura nazywana jest również kamerą otworkową (pinhole camera). Pomimo swojej prostoty, kamera otworkowa jest niezwykle interesującym urządzeniem, które obecnie nadal wykorzystuje się w fotografii artystycznej (pierwsze aparaty fotograficzne były właśnie Camerami Obscura, dopiero później w miejsce otworu wstawiono soczewkę).
Rozdzielczość
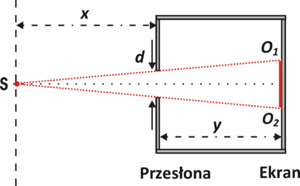
Rozdzielczość układu obrazującego to jego zdolność do zobrazowania dwóch punktowych źródeł światła, znajdujących się w określonej odległości od siebie, jako dwóch oddzielnych obiektów. Powyższa definicja zawiera pojęcie odległości pomiędzy dwoma punktowymi źródłami fali elektromagnetycznej. Jest to jak najbardziej uzasadnione, ponieważ obiekty rzeczywiste (rozciągłe w przestrzeni, emitujące lub odbijające światło), można traktować jako złożenie wielu punktowych źródeł. W przypadku kamery otworkowej, obraz punktowego źródła światła wyznaczymy w oparciu o prawa optyki geometrycznej. Ich podstawowym założeniem jest rozchodzenie się światła w postaci wiązki promieni. W ośrodku jednorodnym promienie te biegną prostoliniowo. Korzystając z tych założeń widzimy, że obrazem punktowego źródła światła na ekranie Camera Obscura jest krążek o średnicy:
jeśli punktowe źródło światła znajduje się bardzo daleko od otworu kamery, średnica krążka na ekranie będzie równa średnicy d otworu:
W przypadku gdy źródła światła znajdują się zbyt blisko siebie, ich obrazy (krążki) nałożą się, uniemożliwiając ich rozróżnienie na obrazie. Przyjmijmy zatem, że dwa punktowe źródła światła będziemy mogli postrzegać na ekranie "Camera Obscura" jako oddzielne obiekty, jeśli odległość s środków krążków (patrz rys. 2), będzie nie mniejsza niż średnica otworu d.
Rozdzielczość układów obrazujących można wyznaczyć na podstawie testów, w których danym urządzeniem obrazuje się pewne wzorce geometryczne. Najczęściej są to równoległe linie, których liczba na jednostkę długości rośnie wzdłuż pewnego kierunku. Przykład takiego wzorca zaprezentowano na rys. 3.
Częstości przestrzenne

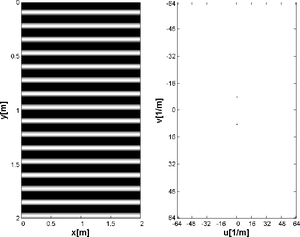
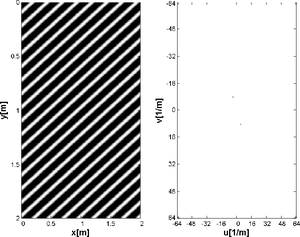
Na rysunku rys. 3 zaprezentowano przykład wzorca stosowanego do wyznaczania rozdzielczości układu obrazującego. Zauważmy, że przedstawiona ilustracja składa się z powtarzających się, w określonej liczbie na jednostkę długości, linii. Inne przykłady obiektów składających się z linii zaprezentowano na rysunkach rys. 4, rys. 5 i rys. 6.
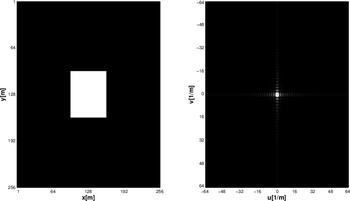
Podobnie jak na rys. 3, na ilustracjach rys. 4, rys. 5 oraz rys. 6 możemy wyróżnić pewne periodycznie powtarzające się struktur, np. na rys. 6 jasne, pionowe linie powtarzają się 8 razy na metr wzdłuż osi x. Z kolei na rys. 5 jasne linie poziome również powtarzają się z częstością 8 razy na metr, tym razem jednak wzdłuż osi y. W przypadku obrazu zaprezentowanego na rys. 6 periodycznie powtarzające się linie są skierowane pod pewnych kątem względem osi x i przecinają tę oś w 4 punktach na
jednostkę długości, zaś oś y w ośmiu punktach na jednostkę długości.
W oparciu o powyższe przykłady, analogicznie jak ma to miejsce w analizie sygnałów jednowymiarowych, dla obiektów przestrzennych i ich obrazów można wprowadzić pojęcie częstości, którą nazwiemy częstością przestrzenną.
Częstość - wielkość określająca, liczbę cykli zjawiska okresowego na jednostce czasu.
Częstość przestrzenna - wielkość określająca, liczbę cykli zjawiska okresowego na jednostkę długości.
Mierzalną wielkością fizyczną przytoczonych ilustracjach jest jasność obiektu.
Dwuwymiarowa Transformata Fouriera
Występujące w przyrodzie sygnały niejednokrotnie charakteryzują się wysokim stopniem złożoności, który utrudnia, a czasami wręcz uniemożliwia badanie ich właściwości. Na rysunkach %i 4 - %i 6 zaprezentowano obrazy o bardzo prostej strukturze. Przykład obrazu o znacznym stopniu złożoności zaprezentowano na rysunku rys. 7. Wzrokowa analiza właściwości tego obrazu jest w zasadzie niemożliwa. Jedną z metod ułatwiających analizę skomplikowanego sygnału, zarówno jedno- jak i dwuwymiarowego, jest dobór odpowiedniej dla niego reprezentacji. Większość spośród stosowanych powszechnie typów reprezentacji ciągłych ma postać tzw. przekształcenia całkowego (inne określenie transformata całkowa). Najczęściej stosowaną transformatą w analizie sygnałów jednowymiarowych jest Transformata Fouriera, za pomocą której analizowany sygnał może być przedstawiony jako suma funkcji harmonicznych. Jest to o tyle istotne, iż funkcje te są niezmiennikami systemów LTI (ang. Linear Time-Invariant), pełniących niezwykle ważna rolę w przetwarzaniu sygnałów. Układy LTI występują również w systemach obrazowania medycznego, co będzie jeszcze omówione w dalszej części materiałów. Pary Transformat Fouriera dla przypadków jedno- i dwuwymiarowych, zarówno ciągłych jak i dyskretnych wyrażają poniższe wzory. Para jednowymiarowych Transformat Fouriera dla sygnału ciągłego [math]x(t)[/math]:
gdzie:
[math]t[/math] — czas,
[math]f[/math] — częstość,
[math]i=\sqrt{-1}[/math],
Para jednowymiarowych dyskretnych Transformat Fouriera dla sygnału dyskretnego:
gdzie:
[math] N[/math] — liczba dyskretnych punktów w sygnale.
Para Transformat Fouriera funkcji ciągłej dwóch zmiennych [math]g(x,y)[/math]:
gdzie:
[math]x, y[/math] — współrzędne przestrzenne,
[math]u, v[/math] — częstości przestrzenne,
[math]i=\sqrt{-1}[/math].
Para Dyskretnych Transformat Fouriera funkcji [math]g(k,l)[/math] dwóch zmiennych dyskretnych [math]k[/math] i [math]l[/math].
gdzie:
[math]M, N[/math] — liczba dyskretnych punktów (liczba wierszy i kolumn w obrazie),
Układy LTI w przetwarzaniu obrazów
Dotychczas pojecie sygnału kojarzyliśmy głównie z przebiegami pewnych wielkości fizycznych w czasie (np. sygnał EEG jest zapisem czynności elektrycznej mózgu). Termin sygnał można także stosować do obrazu. W tym przypadku sygnał jest reprezentacją pewnej mierzalnej cechy obiektu w przestrzeni (na rys. 4 - rys. 6 cechą tą jest rozkład jasności obiektu). Jak pamiętamy z kursu "Analiza Sygnałów", rzeczywiste układy pomiarowe, które realizują przetwarzanie sygnałów nazywamy systemem. System modelowany jest jako czarna skrzynka, generująca odpowiedni sygnał wyjściowy w odpowiedzi na stan wejściowy. Szczególną klasę systemów przetwarzających sygnały, tworzą tzw. Układy Liniowe Niezmiennicze w Czasie (ang. Linear, Time Invariant Systems, LTI). Oznaczmy przez [math]T\left\{\cdot\right\}[/math] operacje wykonywane na sygnałach wejściowych x(t) oraz y(t), wtedy układ LTI charakteryzuje się następującymi własnościami:
- Liniowość.
[math]T\left\{x(t)+y(t)\right\}=T\left\{x(t)\right\}+T\left\{y(t)\right\}[/math][math]T\left\{ax(t)\right\}=aT\left\{x(t)\right\}[/math]
- Niezmienniczość w czasie.
[math]T\left\{x(t+\tau)\right\}=T\left\{x(t)\right\}[/math]
Przykładem układów LTI są filtry typu IIR oraz FIR. Filtry te, jako układu LTI zmieniają amplitudę oraz poszczególnych składowych częstościowych sygnału. Nie mogą natomiast wytworzyć w sygnale składowych o nowych częstościach, co jest charakterystyczną cechą układów nielinowych. Operację przetwarzania sygnału przez układ LTI zapisujemy przy pomocy splotu. Niech x(t) będzie sygnałem na wejściu układu LTI, y(t) sygnałem na jego wyjściu, zaś h(t) odpowiedzią systemu LTI na impuls jednostkowy, wtedy zachodzi następująca relacja:
gdzie [math]\ast[/math] oznacza splot.
Pojęcie układów LTI można rozszerzyć również na sygnały dwuwymiarowe, czyli np. obrazy. Niech g(x,y,) oraz v(x,y) będą dwoma obrazami na wejściu pewnego systemu, realizującego operację [math]T\left\{\cdot\right\}[/math]. System nazwiemy liniowym, jeśli spełni następujące warunki:
- Liniowość.
[math]T\left\{g(x,y)+v(x,y)\right\}=T\left\{g(x,y)\right\}+T\left\{v(x,y)\right\}[/math][math]T\left\{ag(x,y)\right\}=aT\left\{g(x,y)\right\}[/math]
- Niezmienniczość w czasie.
[math]T\left\{g(x,y,t+\tau)\right\}=T\left\{g(x,y,t)\right\}[/math]
Podobnie jak i w przypadku sygnałów jednowymiarowych, przykładem układów LTI w analizie obrazów są filtry cyfrowe. Własności filtrujące posiadają również znane z kursów fizyki soczewki, które działają jak filtry dolnoprzepustowe — usuwają z padającego na nie obrazu składowe o wysokich częstościach, przez co obraz po przejściu przez soczewkę staje się rozmyty. Wiele elementów aparatury stosowanej w obrazowaniu medycznym może być również traktowana jako układy LTI co znacznie ułatwia analizę ich działania. Relację pomiędzy obrazem na wejściu i wyjściu układu LTI można opisać za pomocą dwuwymiarowego splotu. Niech g(x,y) będzie obrazem wejściowym, v(x,y) obrazem na wyjściu systemu LTI, zaś i h(x,y) odpowiedzią układu LTI na punktowe źródło światła, wtedy:
Operację splotu w dziedzinie częstości przestrzennych można zapisać w następujący sposób:
Podobnie jak w analizie sygnałów, funkcję [math]h(x,y)[/math] nazywana jest funkcją odpowiedzi impulsowej lub punktową funkcją rozproszenia (ang. Point Spread Function, PSF). Nazwa jest nieprzypadkowa, ponieważ efektem działania układu optycznego jest rozmycie obrazu obiektu punktowego.
O rozdzielczości raz jeszcze
Pojęcie rozdzielczości układu obrazującego zostało już wprowadzone na przykładzie prostego urządzenia jakim jest "Camera Obscura" oraz punktowych źródeł światła. Obecnie postaramy się omówić pojęcie rozdzielczości w kontekście systemów LTI.
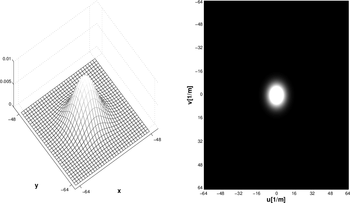
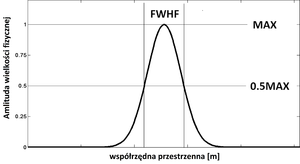
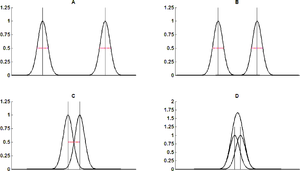
W poprzednim rozdziale dowiedzieliśmy się, że wśród urządzeń służących do obrazowania można wyróżnić niezwykle ważną klasę układów, czyli tzw. systemy LTI. W przypadku układów obrazujących LTI, rolę impulsu jednostkowego pełni punktowe lub nieskończenie wąskie i długie (liniowe) źródło światła. Każdy dwuwymiarowy obiekt można być reprezentowany jako suma punktowych źródeł światła. Z kolei model liniowego (nieskończenie długiego i wąskiego źródła światła) jest wygodny do pomiaru rozdzielczości układu. W takim przypadku rozdzielczość jest to maksymalna liczba linowych źródeł światła na jednostkę długości obrazowanego obiektu, które można rozpoznać jako oddzielne źródła fali elektromagnetycznej. Wiemy już, że układ obrazujący LTI, nie odwzoruje dokładnie rzeczywistych obiektów. Na skutek filtrowania częstości przestrzennych, obrazy obiektów punktowych czy obiektów mający charakter nieskończenie cienkich linii, zostaną rozmyte. Na rysunku rys. 11 zaprezentowano typowy znormalizowany rozkład natężenia światła emitowanego przez obiekt punktowy, po przejściu przez układ LTI. Rozkład ten ma charakter krzywej "dzwonowej". Jako miarę rozmycia obrazu obiektu punktowego przyjmuje się szerokość rozkładu w połowie jego maksymalnej wysokości (ang. Full Width at Half Maximum, FWHM).
Jeśli dwa obiekty punktowe znajdują się blisko siebie, to na skutek rozmycia, mogą być trudne do rozróżnienia na obrazie utworzonym przez układ LTI. Rozdzielczość układu obrazującego zależy od bardzo wielu czynników, które sukcesywnie będą wprowadzane w trakcie poznawania kolejnych metod obrazowania. W tym rozdziale zajmiemy się najważniejszym z parametrów, to jest wielkością FWHM. Nie istnieje ściśle deterministyczny związek pomiędzy parametrem FWHM a rozdzielczością. Można jednak zauważyć, że rozdzielczość jest odwrotnie proporcjonalna do wielkości FWHM, co zaprezentowano na rysunku rys. 12.
Jak wspomniano, rozdzielczość układu obrazującego najczęściej podaje się w liniach, które można rozróżnić na mm. Mierzoną tak rozdzielczość łatwo jest określić za pomocą fantomów, wykonanych np. w przypadku promieniowania RTG z tworzyw sztucznych wewnątrz których rozmieszczone są odpowiednio elementy metalowe (np. druty).
Kontrast. Funkcja Przenoszenia Kontrastu.





Na początku podręcznika zdefiniowaliśmy obraz jako odwzorowanie pewnej cechy obiektu na płaszczyznę. Aby interesujący nas obiekt można było rozpoznać na na obrazie, musi się on różnić pod względem intensywności odwzorowywanej cechy od innych obiektów i tła. Różnicę w natężeniu cechy danego obiektem oraz natężeniu cechy innych przedmiotów lub tła nazywamy kontrastem. Wyróżnia się przy tym pojęcie kontrastu dla rzeczywistych przedmiotów, który nazywamy kontrastem własnym obiektu. Jeśli interesujący nas obiekt charakteryzuje się bardzo niskim kontrastem własnym, zauważenie na nim jakiś szczegółów jest niemożliwe nawet przy użyciu bardzo wysokiej klasy aparatury obrazującej (patrz rys. 15 i rys. 16). Pojęcie kontrastu nie jest w pełni ujednolicone i istnieją różne sposoby jego obliczania. Najczęściej podaje się
- Kontrast globalny.
- gdzie (patrz rys. 13):
- [math]I_A[/math] — maksymalna intensywność cechy fizycznej (np. natężenia światła) w interesującym nas obszarze przestrzeni lub obrazu.
- [math]I_B[/math] — minimalna intensywność cechy fizycznej (np. natężenia światła) w interesującym nas obszarze przestrzeni lub obrazu.
- Kontrast lokalny
- gdzie (patrz rys. 14):
- [math]I_A[/math] — intensywność cechy fizycznej (np. natężenia światła), interesującego nas obiektu rzeczywistego lub jego odwzorowania na obrazie.
- [math]I_B[/math] — intensywność cechy fizycznej (np. natężenia światła) otoczenia (tła) interesującego nas obiektu rzeczywistego lub jego odwzorowania na obrazie.
- Stosunek Kontrastu do Szumu (ang. Contrast To Noise Ratio, CNR).
- gdzie:
- [math]I_A, I_B[/math] — intensywność cechy fizycznej (np. natężenia światła), dwóch interesujących nas obiektów lub ich odwzorowania na obrazie.
- [math]\sigma^2[/math] — wariancja szumu.
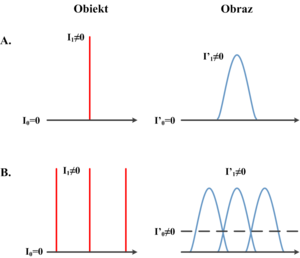
Postrzegany przez nas kontrast zależy od bardzo wielu czynników, m.in. od rozmiarów obiektu i rozmycia jego brzegów. Istotną wpływ ma także szerokość funkcji PSF co zaprezentowano na rys. 17. W przypadku rys. 17.A lokalny kontrast własny obiektu wynosi: [math]C = \frac{I_1 - 0}{0} = \infty[/math]. Urządzenie diagnostyczne utworzyło rozmyty obraz punktowego źródła światła, o maksymalnym natężeniu światła [math]I_1'\lt I_1[/math] i natężeniu tła wnoszącym [math]I_0'=0[/math]. Kontrast lokalny obrazu jest nadal wysoki, ponieważ [math]C = \frac{I'_1 - 0}{0} = \infty[/math], jednak z uwagi na rozmycie brzegów obiektu, obserwator stwierdzi, że kontrast obrazu jest niższy niż kontrast obiektu, co zaprezentowano na rys. 18.
W przypadku rys. 17.B obiekt składa się z trzech źródeł punktowych o kontraście lokalnym dążącym do nieskończoności. W wyniku rozmycia wprowadzonego przez urządzenie diagnostyczne, obrazy poszczególnych źródeł punktowych nakładają się na siebie. Natężenie światła tła na obrazie jest niezerowe, w związku z czym lokalny kontrast [math]C = \frac{I'_1 - I'_0}{I'_0}[/math] osiąga wartość skończoną.
Systemy obrazujące powinny jak najwierniej odwzorowywać kontrast rzeczywistych obiektów. Na skutek niedoskonałości poszczególnych elementów układu obrazującego kontrast własny obiektu jest zniekształcony na obrazie (zwykle kontrast ulega zmniejszeniu). Przykładowo, standardowe soczewki działają jak filtry dolnoprzepustowe. Usuniecie z obrazu wysokich częstości przestrzennych, które odpowiedzialne są za odtwarzanie szczegółów obiektu, powoduje rozmycie jego krawędzi co jak wiemy (patrz rys. 18) skutkuje w obniżeniu kontrastu. Funkcją, za pomocą której opisuje się wpływ elementu układu obrazującego na kontrast jest "Funkcja Przenoszenia Kontrastu"(ang. Contrast Transfer Function, CTF). CTF to stosunek kontrastu na wyjściu układu obrazującego do kontrastu na wejściu tego układu, obliczany dla zadanej linii na jednostkę długości.
gdzie:
[math]C_{wy}\left(\frac{linie}{mm}\right)[/math] — kontrast na wyjściu układu obrazującego, uzyskany dla danej rozdzielczości.
[math]C_{we}\left(\frac{linie}{mm}\right)[/math] — kontrast na wejściu układu obrazującego, uzyskany dla danej rozdzielczości.
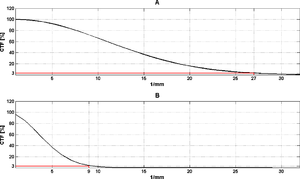
Funkcja Przenoszenia Kontrastu nie osiąga wartości wyższej niż 100% (układy obrazujące mogą zmniejszyć kontrast a nie go poprawić) oraz maleje wraz ze wzrostem z liczbą linii na jednostkę długości. Przykład wykresu funkcji CTF zaprezentowano na rysunku rys. 20. W oparciu o krzywą CTF można zdefiniować rozdzielczość układu obrazującego.
Rozdzielczość układu obrazującego jest to taka liczba linii na jednostkę długości dla której kontrast spada poniżej pewnej ustalonej wartości. Zwykle graniczna wartość kontrastu ustalona jest na poziomie 3%.
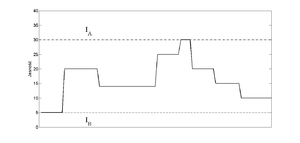
Powyższy sposób określania rozdzielczości układu obrazującego ma następujące uzasadnienie. Kontrast z definicji to różnica w intensywności odwzorowywanej cechy poszczególnych elementów obrazowanej przestrzeni lub obrazu. Jeśli układ obrazujący, na skutek swoich wad, pomniejsza tę różnicę, obiekty są coraz trudniej odróżnialne, zwłaszcza jeśli znajdują się w niewielkiej od siebie odległości. Jeśli kontrast własny obiektu zostanie zmniejszony przez układ obrazujący do pewnej, bardzo niskiej wartości, dwa obiekty położone blisko siebie przestaną być rozróżnialne. Efekt ten zaprezentowano na rys. 19, na którym rzeczywisty obiekt składa się z periodycznie powtarzających się jasnych i ciemnych pionowych linii (%i.A 19). Na rysunku (%i.B 19) pokazano przebieg jasności obiektu wzdłuż osi poziomej. Jak można zauważyć, globalny kontrast obiektu wynosi:
- [math] C = \frac{3.0-2.0}{3.0+2.0} = 0.2[/math].
Na %i.C 19 i %i.D 19 zaprezentowano - odpowiednio: odwzorowanie obiektu zaprezentowanego na %i.A 19 za pomocą układu LTI oraz przebieg jasności światła wzdłuż osi poziomej na obrazie obiektu. Jak można zauważyć, układ LTI odfiltrował wysokie częstotliwości przestrzenne, co doprowadziło do rozmycia brzegów linii. Kontrast uzyskany na obrazie (%i.D 19) wynosi: C = 0.185. Układ LTI odwzorował zatem około 92% (0.185/0.2 x 100) kontrastu własnego rzeczywistego obiektu. Na %i.E 19 i %i.F 19 zaprezentowano obraz obiektu z %i.A 19 otrzymany za pomocą kolejnego układu LTI oraz przebieg jasności światła wzdłuż osi poziomej na obrazie. Zastosowany układ obrazujący znacznie silniej odfiltrował wysokie częstości przestrzenne niż poprzedni system. Kontrast uzyskany na obrazie (%i.D 19) wynosi: C = 0.155. Układ LTI odwzorował zatem około 77% kontrastu własnego rzeczywistego obiektu. Zaprezentowany na rysunku %i.G 19 obraz obiektu z %i.A 19 charakteryzuje się największym rozmyciem brzegów linii i najgorszym kontrastem. Pionowe linie są trudne do odróżnienia od tła. Jak można zauważyć na %i.H 19, kontrast obiektu jest bardzo niski i wynosi C = 6%. Zastosowany układ LTI przeniósł zatem jedynie 3% kontrastu własnego rzeczywistego obiektu.
Modulacja. Funkcja przenoszenia Modulacji.
Główną zaletą opisanej w poprzednim rozdziale Funkcji Przenoszenia Kontrastu jest prostota jej wyznaczenia. Do tego celu można wykorzystać odpowiednie przygotowane fantomy. Niestety, funkcja ta posiada również pewne wady:
- Przenoszenie kontrastu wyznaczane jest w funkcji linii na jednostkę długości. Rzeczywiste obiekty (zwłaszcza tkanki z jakich składa się organizm) rzadko jednak składają się z linii.
- Systemy obrazujące składają się z bardzo wielu elementów, które niejednokrotnie można opisać przy pomocy formalizmu systemów LTI.
Przykładowo, głównymi elementami odpowiedzialnymi za utworzenie obrazu w aparacie fotograficznym jest obiektyw oraz film (lub matryca CCD). Obiektyw składa się zwykle z wielu soczewek. Załóżmy, że każda z soczewek film lub matryca CCD, funkcjonuje jak układ LTI. Nawet jeśli znamy przebieg funkcji CTF dla każdego z tych elementów, to nie można na tej podstawie przewidzieć wielkości kontrastu uzyskanego na obrazie. Taką informację otrzyma się dopiero badając układ obrazujący jako całość.
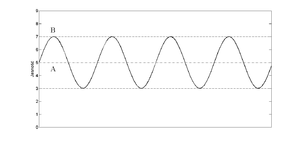
W celu dogodniejszego opisu właściwości urządzenia obrazującego została wprowadzona tzw. Funkcja Przenoszenia Modulacji (ang. Modulation Transfer Function, MTF). Omówienie tej funkcji zaczniemy od przypomnienia pojęcia głębokości modulacji. Załóżmy, iż zmiany jasności pewnego obiektu zachodzą wzdłuż jednego z jego boków z częstością u. Amplituda zmian jasności, wokół pewnego stałego poziomu A, wynosi B. Zmiany jasności obiektu, które wyraża następujący wzór:
zaprezentowano na rys rys. 21. Współczynnik głębokości modulacji to wielkość, która określa zmiany pewnego parametru względem pewnej stałej wartości. Jak widzimy na rys rys. 21 zmiany jasności obiektu osiągają amplitudę B względem pewnego poziomu jasności A. W takim przypadku współczynnik głębokości modulacji określa poniższy wzór:
Wykonajmy teraz obraz obiektu za pomocą układu LTI. Przypominamy, że układ LTI może zmieniać amplitudę i fazę poszczególnych częstości przestrzennych. W związku z tym, na wyjściu układu otrzymamy obraz [math]g(x,y)[/math], którego zmiany jasności będą opisane wzorem:
natomiast współczynnik modulacji wyniesie:
Możemy zbadać teraz, jak układ LTI przeniósł współczynnik głębokości modulacji w następujący sposób:
Im wartość współczynnika ‘‘H’’ jest bliższa jedności, tym układ LTI wiernej odwzorował na obrazie zmiany zachodzące w jasności obiektu.
Zmiany w jasności, czy też innych cechach rzeczywistych obiektów są jednak znacznie bardziej skomplikowane niż powyższy przykład.
Jednakże, zarówno rzeczywiste obiekty, jak też ich obrazy, możemy przedstawić jako szereg harmonicznych oscylacji przestrzennych. Załóżmy, iż obiekt, zmiany jasności opisuje funkcja [math]f(x,y)[/math] oraz jego obraz [math]g(x,y)[/math] rozłożyliśmy na Szereg Fouriera:
gdzie:
[math]x, y[/math] - współrzędne przestrzenne,
[math]u_i, v_j[/math] - i-ta oraz j-ta częstości przestrzenna,
[math]A, B_{ij}, C, D_{ij}[/math] - amplitudy poszczególnych składowych harmonicznych.
Niech obiekt f(x,y) o widmie F(u,v) zostanie odwzorowany za pomocą układu LTI na obrazie [math]g(x,y)[/math] o widmie [math]G(u,v)[/math]. Układ LTI scharakteryzowany jest przy pomocy funkcji odpowiedzi impulsowej h(x,y) o widmie [math]H(u,v)[/math]. Z własności układów LTI wiemy, iż pomiędzy stanem wejściowym (obrazowanym obiektem) a wyjściem (obrazem) istnieje następujący związek:
Przypominamy również, że moduł Transformaty Fouriera odpowiada amplitudzie danej składowej harmonicznej, w związku z czym możemy zapisać:
Korzystając z powyższych zależności możemy zapisać:
W przypadku obiektu złożonego z wielu składowych harmonicznych, głębokość modulacji może być inna dla każdej częstości przestrzennej:
Zauważmy teraz, iż głębokość modulacji [math]m^g_{u_i,v_j}[/math] obrazu g(x,y) można wyrazić w następujący sposób:
Zbadajmy teraz, jak głębokość modulacji [math]m^f_{u_i,v_j}[/math] rzeczywistego obiektu została odwzorowana na obrazie. Głębokość modulacji obrazu oznaczmy [math]m^g_{u_i,v_j}[/math]
Wielkość opisującą stosunek głębokości modulacji dla zadanych częstości przestrzennych w obrazie, do głębokości modulacji dla tych samych częstości przestrzennych w rzeczywistym obiekcie nazywamy Funkcją Przenoszenia Modulacji (MTF):
Funkcję MTF układu LTI można w w łatwy sposób wyznaczyć, jeśli znamy widmo odpowiedzi tego systemu na impuls jednostkowy.
Funkcja Przenoszenia Modulacji a rozdzielczość przestrzenna.

Linie x ft.png Obiekt zaprezentowany na rys. 22 może zostać opisany za pomocą jednej funkcji harmonicznej biegnącej wzdłuż osi X:
gdzie: [math]u_0=32\frac{\textrm{1}}{\textrm{m}}[/math].
Maksima funkcji harmonicznej tworzą pionowe jasne linie. Odległość pomiędzy tymi liniami [math]\Delta x[/math] jest odwrotnością częstości przestrzennej funkcji harmonicznej [math]u_0[/math]:
Obraz g(x,y) obiektu f(x,y) może być rozłożony na składowe harmoniczne w następujący sposób:
Związek pomiędzy składowymi harmonicznymi obrazu g(x,y) na wyjściu układu LTI, a składowymi harmonicznymi rzeczywistego obiektu f(x,y) na wejściu tego układu, wyraża poniższa zależność
gdzie: MTF jest funkcja przenoszenia modulacji charakterystyczną dla zadanego systemu LTI. Jeśli dla danej częstości przestrzennej [math]u_0[/math], funkcja przenoszenia modulacji [math]MTF(u_0,0)[/math] osiąga wartość bliską 0, częstość ta nie zostanie odwzorowana na obrazie. W związku z tym niemożliwe będzie rozróżnienie szczegółów znajdujących się bliżej niż [math]\Delta x = \frac{1}{u_0}[/math]. W praktyce przyjmuje się, że graniczna rozdzielczość przestrzenna układu obrazującego osiągana jest dla częstości, dla której wartość funkcji przenoszenia modulacji wynosi 0.03.
Funkcja Przenoszenia Modulacji a przenoszenie kontrastu.
Na początku rozpatrzmy następujący przykład. Zamierzamy odwzorować cechę pewnego obiektu, jaką jest rozkład jego jasności. Ponadto zmiany jasności obiektu f(x,y) można opisać za pomocą jednej funkcji harmonicznej:
Obiekt taki zaprezentowano na rys. 22, w przypadku którym A = 3, B=1. Przyjęte założenia mają na celu uprościć pewne przekształcenia matematyczne, nie wpłyną jednak na końcowe wnioski jakie uzyskamy w niniejszym przykładzie. Zdefiniujmy teraz kontrast globalny w następujący sposób:
gdzie:
[math] A_{\max}, A_{\min}[/math] to odpowiednio maksymalna i minimalna amplituda zmian obserwowana w sygnale.
Obliczmy kontrast globalny obiektu opisanego wzorem (%i 39):
Jak możemy zauważyć, uzyskany kontrast jest tożsamy z głębokością modulacji sygnału harmonicznego, który wynosi:
Modulacja sygnału jest wielkością, której przenoszenie przez układ LTI opisuje funkcja MTF. Doszliśmy zatem do wniosku, iż funkcja MTF pośrednio opisuje przenoszenie kontrastu zawartego w sygnale przez układ LTI.
Funkcja MTF złożonych układów obrazowania
Układu wykorzystywane w obrazowaniu medycznych są zbudowane z bardzo wielu elementów (źródeł promieniowania, układów formujących wiązki promieniowania, detektorów, itd.), które mają wpływ na uzyskiwany obraz. Nawet w budowie zwykłego aparatu fotograficznego możemy wyróżnić kilka podzespołów, takich jak obiektyw oraz detektor promieniowania (film lub matrycę CCD). Obiektyw z kolei złożony jest najczęściej z przesłony i kilku soczewek, których działanie może być opisane w formalizmie systemów LTI. Czy znając funkcję MTF dla każdego z elementów układu obrazującego jesteśmy w stanie coś wywnioskować na temat jakości obrazu uzyskanego przez cały układ obrazujący? Okazuje się że tak. Załóżmy, że nasz system obrazujący składa się z N bloków (czarnych skrzynek), z których każda może być opisana jako układ LTI. Schemat takiego urządzenia zaprezentowano na rys. 23. Właściwości każdego z elementów układu obrazującego w dziedzinie częstości przestrzennych opisane są przy pomocy funkcji przejścia [math]H_i(u,v)[/math], gdzie u,v to częstości przestrzenne. Na wejściu układu obrazującego podawany jest sygnał o widmie [math]F(u,v)[/math]. Trafia on jednocześnie na wejście pierwszego układu LTI. Na wyjściu pierwszego układu LTI sygnał będzie miał postać:
Sygnał wyjściowy z pierwszego układu LTI jest sygnałem wejściowym dla kolejnego układu. W związku z tym, na wyjściu drugiego układu LTI pojawi sygnał:
Ostatecznie, po przejściu przez N układów LTI, na wyjściu układu obrazującego uzyskamy sygnał:
Dla całego układu obrazującego możemy zatem zdefiniować następująca funkcję przejścia:
i wyznaczyć funkcję MTF tego układu:
Funkcję MTF można również wyznaczyć znając przebieg funkcji przenoszenia modulacji [math]MTF_i(u,v) = \frac{H_1(u,v)}{ H_1(0,0)}[/math] każdego systemu LTI wchodzącego w skład układu obrazującego, co wynika ze wzoru (%i 44):
Zalety Funkcji MTF
- Na podstawie przebiegu funkcji MTF można określić graniczną rozdzielczość układu obrazującego. Im lepiej układ LTI przenosi głębokość modulacji sygnału wejściowego dla wysokich częstości przestrzennych, tym lepsza będzie rozdzielczość otrzymywanego na wyjściu obrazu.
- Na podstawie przebiegu funkcji MTF można określić jak układ LTI odwzorowuje kontrast zawarty w sygnale wejściowym.
- Znając przebieg funkcji MTF dla poszczególnych składowych układu obrazującego można estymować funkcję MTF dla całego układu i przewidzieć jego właściwości.
Wyznaczanie funkcji MTF na przykładzie Kamery Otworkowej
Przypominamy na początku, że działanie systemu obrazującego o własnościach układu LTI można opisać następującym wzorem:
gdzie:
- * oznacza operację splotu,
- g(x,y) – reprezentacja obiektu na wejściu układu obrazującego,
- g(x,y) – reprezentacja obiektu na wyjściu układu obrazującego,
- h(x,y) – odpowiedź układu obrazującego na pobudzenie punktowym źródłem światła.
Funkcję [math]h(x,y)[/math] nazywamy punktową funkcja rozproszenia (ang. Point Spread Function,PSF). Transformatę Fouriera [math] OTF(u,v)[/math] funkcji PSF:
nazywamy optyczną funkcją przenoszenia (ang. Optical Transfer Function,OTF). Funkcję OTF tę można zapisać w następujący sposób:
gdzie: [math]\phi(u,v) = \arg(OTF(u,v))[/math].
Moduł Transformaty Fouriera funkcji PSF, znormalizowany w ten sposób, aby [math]|OTF(0,0)| = 1[/math] nazywamy funkcją przenoszenia modulacji:
z kolei argument funkcji OTF nazywamy funkcją przenoszenia fazy (ang. Phase Transfer Function,PTF):
Przykład wyznaczenia funkcji MTF dla Kamery Otworkowej
Obrazem punktowego źródła światła, znajdującego się w nieskończonej odległości od kamery otworkowej jest krążek o średnicy d równej średnicy obiektywu (otworka) kamery i równomiernym rozkładzie natężenia światła A, który możemy opisać następującym wzorem:
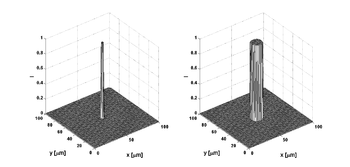
Rozkład natężenia światła emitowanego z punktowego źródła oraz jego obraz (funkcję PSF) zaprezentowano na rys. 24. Transformata Fouriera funkcji PSF(x,y) wynosi:
gdzie:
- [math]J_1(\cdot)[/math] — to funkcja Bessla pierwszego rodzaju, rzędu pierwszego,
- [math]\rho=\sqrt{u^2 + v^2}[/math],
- [math]u,v[/math] — częstości przestrzenne.
Funkcja przenoszenia modulacji – MTF, to moduł znormalizowanej funkcji OTF. Wartość funkcji OTF w punkcie [math](0,0)[/math] wynosi [math]\frac{1}{2}[/math], w związku z czym funkcja MTF jest równa:
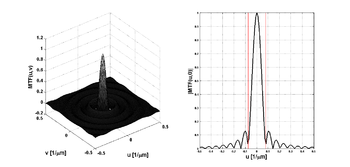
Wykres funkcji OTF oraz MTF zaprezentowano na rys. 25. Funkcja MTF osiąga pierwsze miejsce zerowe dla argumentu równego
Wielkość [math]\rho_g[/math] to górna granica pasma częstości przestrzennych przenoszonych przez Kamerę Otworkową.