Aliasing: Różnice pomiędzy wersjami
| Linia 1: | Linia 1: | ||
==[[Analiza_sygnałów_-_lecture|AS/]] Przekształcenie Fouriera sygnałów dyskretnych, aliasing== | ==[[Analiza_sygnałów_-_lecture|AS/]] Przekształcenie Fouriera sygnałów dyskretnych, aliasing== | ||
| − | ===[[Media:aliasing.ogv|''' | + | ===[[Media:aliasing.ogv|'''Animacja pokazująca efekt aliasingu''']]=== |
| − | + | [[Media:aliasing.ogv|'''Kliknij na tym napisie aby obejrzeć animację pokazującą efekt aliasingu na sygnale jednowymiarowym''']] | |
| − | [[ | + | [[Plik:aliasingklatka.png]] |
| + | |||
| + | ===Próbkowanie odwrotnej transformaty Fouriera=== | ||
Przypomnijmy [[Przekształcenie Fouriera#label-eq:21|wzór na odwrotną transformację Fouriera]] sygnału ciągłego | Przypomnijmy [[Przekształcenie Fouriera#label-eq:21|wzór na odwrotną transformację Fouriera]] sygnału ciągłego | ||
| Linia 38: | Linia 40: | ||
<math>\Delta t</math>. | <math>\Delta t</math>. | ||
| − | Innym sposobem pokazania | + | |
| + | ===Splot z grzebieniem Diraca=== | ||
| + | Innym sposobem pokazania powyższego efektu jest przedstawienie sekwencji dyskretnej <math>s[n]</math> jako iloczynu sygnału ciągłego <math>s(t)</math> z grzebieniem Diraca | ||
<math> | <math> | ||
| Linia 61: | Linia 65: | ||
sygnału ciągłego, przesuwanej o wielokrotności odwrotności | sygnału ciągłego, przesuwanej o wielokrotności odwrotności | ||
<math>\Delta t</math>. | <math>\Delta t</math>. | ||
| + | |||
| + | |||
| + | Poniższy przykład ilustruje aliasing w dziedzinie czasu: | ||
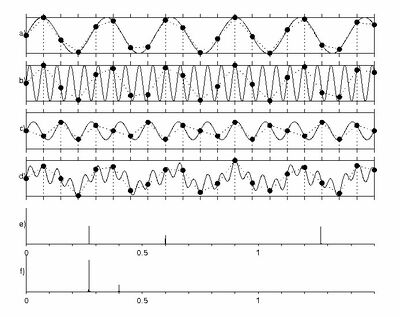
[[Plik:klasyczna_rys_5.jpg|thumb|center|400px|<figure id="fig:36"></figure>Próbkowanie (<math>\Delta t = 1</math>) sygnałów o częstościach: (a) 0.27, (b) 1.27 i (c) 0.6. | [[Plik:klasyczna_rys_5.jpg|thumb|center|400px|<figure id="fig:36"></figure>Próbkowanie (<math>\Delta t = 1</math>) sygnałów o częstościach: (a) 0.27, (b) 1.27 i (c) 0.6. | ||
| Linia 74: | Linia 81: | ||
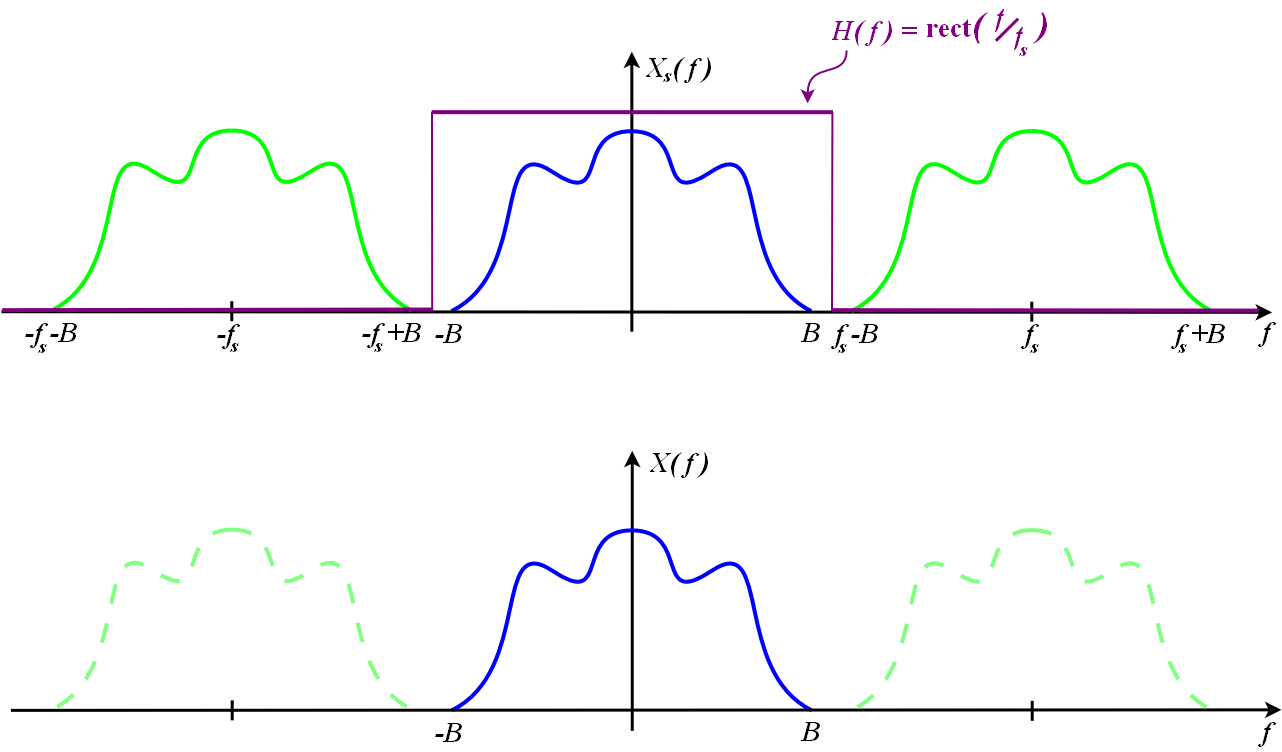
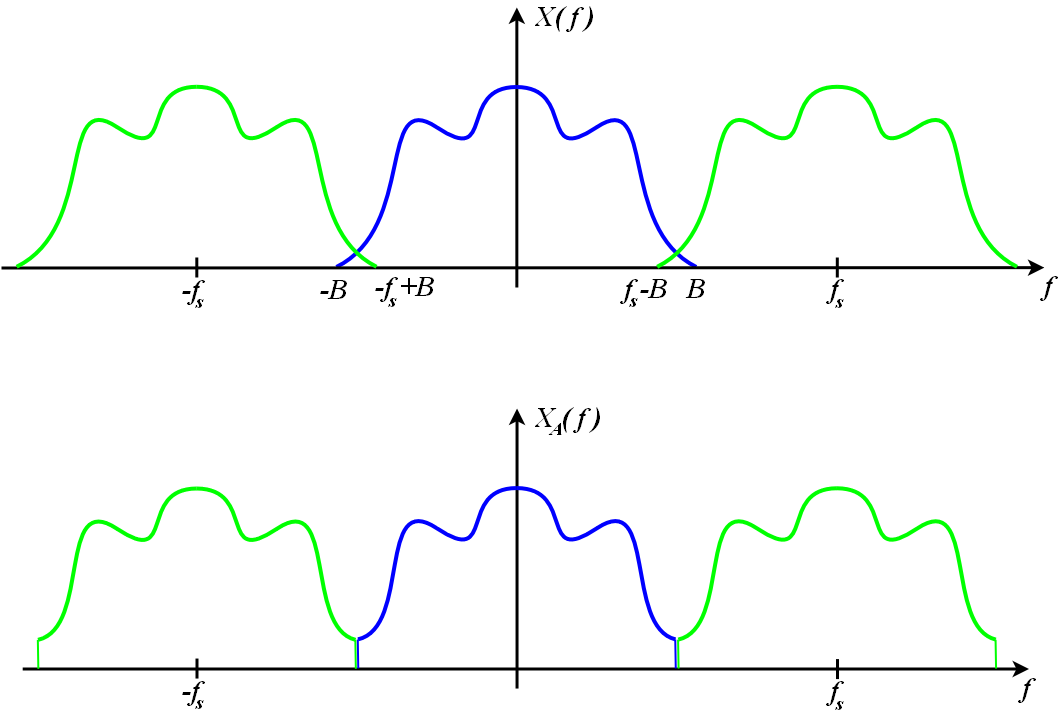
| + | Kolejne dwa rysunki z Wikipedii ilustrują ten efekt w dziedzinie częstości, dla przypadku próbkowania z częstością większą i mniejszą od częstości Nyquista: | ||
| + | |||
| + | [[Plik:ReconstructFilter.png|width=400]] | ||
| + | [[Plik:AliasedSpectrum.png|width=400]] | ||
<references/> | <references/> | ||
Wersja z 12:31, 25 paź 2015
Spis treści
AS/ Przekształcenie Fouriera sygnałów dyskretnych, aliasing
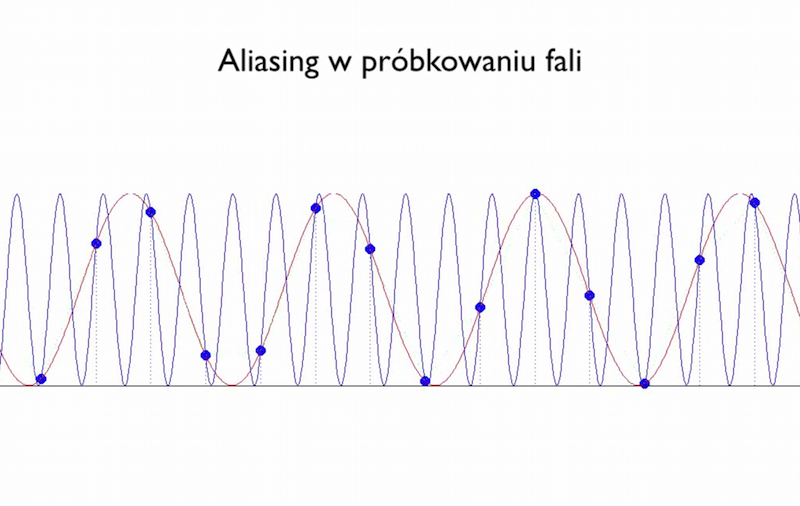
Animacja pokazująca efekt aliasingu
Kliknij na tym napisie aby obejrzeć animację pokazującą efekt aliasingu na sygnale jednowymiarowym
Próbkowanie odwrotnej transformaty Fouriera
Przypomnijmy wzór na odwrotną transformację Fouriera sygnału ciągłego [math] s(t)=\int_{-\infty}^{\infty}\hat{s}(f)e^{-i 2\pi t f} d f [/math]
Dyskretne wartości tego sygnału, próbkowane w chwilach [math]n \Delta t[/math], możemy odtworzyć z powyższgo równania dla [math]t = n \Delta t[/math]
[math] \sum_{r=-\infty}^\infty \int_\frac{(2r - 1)}{2\Delta t}^\frac{(2r + 1) }{2\Delta t} \hat{s}(f)e^{-i 2\pi n \Delta t f} d f \;\; \stackrel{f \rightarrow f+\frac{r}{\Delta t}}{=} \;\; [/math] [math] \sum_{r=-\infty}^\infty \int_\frac{-1}{2\Delta t}^\frac{1}{2\Delta t} \hat{s}\left(f + \frac{r}{\Delta t}\right)e^{-i 2\pi n \Delta t (f + \frac{r}{\Delta t})} d f [/math]
[math] = \int_\frac{-1}{2\Delta t}^\frac{1}{2\Delta t} \sum_{r=-\infty}^\infty \hat{s}\left(f + \frac{r}{\Delta t}\right)e^{-i 2\pi n \Delta t f} d f [/math]Szukając wartości sygnału w dyskretnych chwilach czasu, dostaliśmy w miejsce odwrotnej transformaty Fouriera całkę w ograniczonym zakresie z funkcji będącej (nieskończoną) sumą powtórzeń transformaty Fouriera sygnału ciągłego, przesuwanej o wielokrotności odwrotności [math]\Delta t[/math].
Splot z grzebieniem Diraca
Innym sposobem pokazania powyższego efektu jest przedstawienie sekwencji dyskretnej [math]s[n][/math] jako iloczynu sygnału ciągłego [math]s(t)[/math] z grzebieniem Diraca
[math] D(t) = \sum_{k=-\infty}^{\infty} \delta(t-k\delta t) [/math]
Zgodnie z twierdzeniem o splocie, iloczyn w przestrzeni czasu będzie odpowiadał splotowi w dziedzinie częstości, czyli w dziedzinie częstości otrzymamy splot transformaty Fouriers sygnału [math]\hat{s}(t)[/math] z transformatą Fouriera grzebienia Diraca [math]\hat{D}(t)[/math], którą poniżej wyliczymy:
[math] \hat{D}(f) = \mathcal{F}(D(t)) = \mathcal{F}\left(\sum_{k=-\infty}^{\infty} \delta(t-k\Delta t) \right) = \int_{-\infty}^{\infty} \sum_{k=-\infty}^{\infty} \delta(t-k\Delta t) e^{i 2\pi f t} dt = [/math] [math] \sum_{k=-\infty}^{\infty} \int_{-\infty}^{\infty} \delta(t-k\Delta t) e^{i 2\pi f t} dt = \sum_{k=-\infty}^{\infty} e^{i 2\pi f k\Delta t} [/math]
Otrzymaliśmy ogólny wynik -- transformata Fouriera grzebienia Diraca to również grzebień Diraca (w przestrzeni częstości).
Przypomnijmy (np. z rozważań o systemach liniowych niezmienniczych w czasie), że splot z deltą Diraca w zerze jest identycznością, a splot z [math]\delta(t-kT)[/math] przesuwa funkcję o [math]kT[/math]. Z liniowości splotu dostajemy -- jak pozyżej -- sumę powtórzeń transformaty Fouriera sygnału ciągłego, przesuwanej o wielokrotności odwrotności [math]\Delta t[/math].
Poniższy przykład ilustruje aliasing w dziedzinie czasu:
Kolejne dwa rysunki z Wikipedii ilustrują ten efekt w dziedzinie częstości, dla przypadku próbkowania z częstością większą i mniejszą od częstości Nyquista: