WnioskowanieStatystyczne/Momenty

Wnioskowanie_Statystyczne_-_wykład

Wariancja, korelacja, mediana

Jak widać, własności rozkładów ciągłych i dyskretnych będą opisywać nieco odmienne wzory; poniżej przytaczamy najczęściej wykorzystywane w praktyce definicje i zależności.

Wartość oczekiwana

Zgodnie z nazwą i intuicją, wartość oczekiwana określa środek rozkładu, czyli okolicę, w którą najczęściej powinny "trafiać" wyniki. Dla rozkładów dyskretnych będzie się ona wyrażać wzorem:

[math] \mu=E(x)=\overset{n}{\underset{i=1}{\sum }}x_{i}P(X=x_{i}) [/math]

a dla rozkładów ciągłych:

[math] \mu=E(x)=\underset{-\infty }{\overset{\infty }{\int }}x p(x)dx. [/math]

Na podstawie tych wzorów łatwo dowieść liniowości wartości oczekiwanej; dla zmiennych losowych [math]x[/math] i [math]y[/math] oraz stałych [math]c_1[/math] i [math]c_2[/math]

[math] E(c_1 x+c_2 y)=c_1 E(x)+c_2 E(y). [/math]

Mediana

Mediana to inna od wartości oczekiwanej miara położenia środka rozkładu. Określamy ją jako taką wartość zmiennej losowej [math]x_{\frac{1}{2}}[/math], która dzieli rozkład gęstości prawdopodobieństwa na dwie równe części — wartościom zmiennych losowych mniejszym niż [math]x_{\frac{1}{2}}[/math] odpowiada tyle samo przypadków, co wartościom większym:

[math] \int\limits_{-\infty}^{x_{\frac{1}{2}}} p(x) dx = \int\limits_{x_{\frac{1}{2}}}^\infty p(x) dx= \ \frac{1}{2}. [/math]

Dla rozkładów symetrycznych mediana i wartość oczekiwana są sobie równe.

Wariancja

Wariancja jest miarą rozrzutu zmiennej losowej wokół wartości oczekiwanej, czyli "szerokości" rozkładu prawdopodobieństwa. Mała wariancja oznacza, że zmienne (np. wyniki losowań) będą gromadzić się ("wypadać") blisko wartości oczekiwanej (i blisko siebie).

Wariancję określamy jako wartość oczekiwaną kwadratu różnicy zmiennej i jej wartości oczekiwanej; dla rozkładów dyskretnych:

[math] \sigma ^{2}(x)=E((x-\mu)^{2})=\overset{n}{\underset{i=1}{\sum }} P(X=x_{i})(x_{i}-\mu)^{2}. [/math]

Dla rozkładów ciągłych:

[math] \sigma ^2(x)=E((x-\mu)^{2})=\underset{-\infty }{\overset{\infty }{ \int }}(x-\mu)^{2} p(x)dx. [/math]

Pierwiastek wariancji [math]\left( \sigma=\sqrt{\sigma^2}\right)[/math] nosi nazwę odchylenia standardowego.

Wyprowadzimy jeszcze jeden ogólny wzór na obliczanie wariancji, użyteczny w wielu przypadkach:

[math] \sigma ^{2}(x)= \sigma^2_x = E(x^{2})-\left\{ E(x)\right\} ^{2}. [/math]

Dowód

[math] \sigma^{2}(x)=E((x-\mu )^{2})=E(x^{2}-2x\mu+\mu ^{2})=E(x^{2})-2\mu E(x)+\mu^{2}=E(x^{2})-\mu^{2}=E(x^{2})-\left\{ E(x)\right\} ^{2} [/math]

Czyli wariancja zmiennej losowej jest równa różnicy wartości oczekiwanej kwadratu tej zmiennej i kwadratu jej wartości oczekiwanej.

Kowariancja i współczynnik korelacji

Przykładowe wartości współczynnika korelacji dla 300 par [math](x, y)[/math] o różnych stopniach współzależności.

Miarą związku między zmiennymi [math]x[/math] i [math]y[/math] jest kowariancja

[math] \sigma_{x, y} = E\left( (x-\mu_{x})(y-\mu_{y})\right) [/math]

lub unormowany do jedności współczynnik korelacji zmiennych [math]x[/math] i [math]y[/math]:

[math] \rho_{x, y}= \frac{\sigma_{x, y}}{\sigma_x \sigma_y}= \frac{E\left( \left(x-\mu_{x})(y-\mu_{y}\right)\right)} {\sqrt{E\left( (x-\mu_{x})^2\right) E\left( (y-\mu_{y})^2\right)}}, [/math]

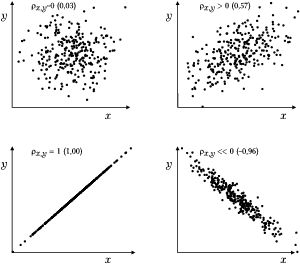
gdzie [math]\mu_x[/math] i [math]\mu_y[/math] to odpowiednio wartości oczekiwane zmiennych [math]x[/math] i [math]y[/math]. Jeśli zmienne [math]x[/math] i [math]y[/math] związane są deterministyczną zależnością liniową (typu [math]y=c_1 x+c_2[/math]), to ich korelacja wynosi [math]1[/math] (lub [math]-1[/math], jeśli [math]c_1\lt 0[/math]). Jeśli wzrostowi zmiennej [math]x[/math] towarzyszy statystycznie wzrost zmiennej [math]y[/math], to ich korelacja jest dodatnia (pomiędzy [math]0[/math] a [math]1[/math]). Dla zmiennych niezależnych korelacja wynosi [math]0[/math].

---