AS cwiczenia DTF: Różnice pomiędzy wersjami
(Utworzono nową stronę "==Wielokanałowe modele AR== Model autoregresyjny rozpatrywaliśmy do tej pory jako proces generacji pojedynczego sygnału ''x''. Nic jednak nie stoi na przeszkodzie, ab...") |
|||
| (Nie pokazano 5 pośrednich wersji utworzonych przez tego samego użytkownika) | |||
| Linia 1: | Linia 1: | ||
| + | <!-- | ||
| + | https://web.archive.org/web/20111023232716/http://eeg.pl:80/DTF/beta_finger_2d.html | ||
| + | --> | ||
| + | === Korelacja i funkcja korelacji=== | ||
| + | Dla przypomnienia: zagadnienia te poruszane były na [[Twierdzenia_o_splocie_i_o_próbkowaniu_(aliasing)#Korelacja_i_splot|wykładzie]] | ||
| + | |||
| + | Kowariancja: | ||
| + | |||
| + | ::<math>\sigma _{xy} = \int {(x(t)-\bar{x}) (y(t)-\bar{y}) dt }</math> | ||
| + | |||
| + | Kowariancja dwóch zmiennych losowych jest miarą tego na ile dwie zmienne losowe mają podobne tendencje do zmian. | ||
| + | Przykład: w zmiennej <tt>x</tt> parami podajemy wartość pierwszej i drugiej zmiennej | ||
| + | <tt> | ||
| + | x = np.array([[0, 2], [1, 1], [2, 0]]).T | ||
| + | </tt> | ||
| + | W tej postaci łatwo zauważyć, że gdy pierwsza zmienna rośnie to druga maleje: | ||
| + | >>> x | ||
| + | array([[0, 1, 2], | ||
| + | [2, 1, 0]]) | ||
| + | Tę własność naszych zmiennych wyrażają elementy pozadiagonalne macierzy kowariancji: | ||
| + | >>> np.cov(x) | ||
| + | array([[ 1., -1.], | ||
| + | [-1., 1.]]) | ||
| + | |||
| + | |||
| + | |||
| + | Współczynnik normalizacyjny: | ||
| + | |||
| + | ::<math>\sigma _{ss} = \int {\left(s(t)-\bar{s}\right)^2 dt}</math> | ||
| + | Implementacja w Pythonie: [http://docs.scipy.org/doc/numpy/reference/generated/numpy.cov.html#numpy.cov numpy.cov] | ||
| + | |||
| + | |||
| + | Korelacja | ||
| + | ::<math>\rho _{xy}= \frac{\sigma _{xy}}{\sqrt{\sigma _{xx} \sigma _{yy}}}</math> | ||
| + | |||
| + | Implementacja w Pythonie: [http://docs.scipy.org/doc/numpy/reference/generated/numpy.corrcoef.html numpy.corrcoef] | ||
| + | |||
| + | |||
| + | ===Badanie zależności między sygnałami przy pomocy funkcji korelacji=== | ||
| + | <source lang = python> | ||
| + | def gabor(t0=0.5, sigma = 0.1, f = 10, T = 1, Fs = 128, phi =0 ): | ||
| + | dt = 1.0/Fs | ||
| + | t = np.arange(0,T,dt) | ||
| + | s = np.exp( -0.5*((t-t0)/sigma)**2 )*np.cos(2*np.pi*f*t + phi) | ||
| + | return (s,t) | ||
| + | </source> | ||
| + | # wygeneruj dwa sygnały długości <math>T=2s</math> próbkowane z częstością <math>f_s=128</math> Hz przy uzyciu funkcji <tt>gabor</tt>. Oba gabory mają częstość <math>f=10</math> Hz i <math>\sigma =0.1</math> s. Oba sygnały <tt>s1</tt> i <tt>s2</tt> są centrowane na <math>t_0=0.5</math> s | ||
| + | # oblicz funkcję korelacji wzajemnej <tt>z = np.correlate(s1,s2,mode='full')</tt> | ||
| + | # Jaka jest długość sygnału <tt>z</tt>? | ||
| + | # Wykreśl w funkcji odpowiednich skal czasu na dwóch subplotach: na górnym sygnały <tt>s1</tt> i <tt>s2</tt> a na dolnym <tt>z</tt>. | ||
| + | # Zaobserwuj położenie maksimum funkcji korelacji wzajemnej. Jaki jest związek oscylacji w funkcji korelacji wzajemnej z oscylacjami funkcji <tt>s1</tt> i <tt>s2</tt> | ||
| + | |||
| + | Wskazówka: Związek między czasem <tt>t</tt> dla sygnałów <tt>s1</tt> i <tt>s2</tt> a skalą czasu dla korelacji <tt> f_corr_t</tt> można zapisać w Pythonie: | ||
| + | <source lang = python> | ||
| + | f_corr_t = np.zeros(2*len(t)-1) | ||
| + | f_corr_t[0:len(t)]= -t[len(t)::-1] | ||
| + | f_corr_t[len(t):]=t[1:] | ||
| + | </source> | ||
| + | |||
| + | |||
| + | *Powtórz punkty 1-5 zmieniając położenie sygnału <tt>s1</tt> od 0.5 do 0.1 z krokiem 0.1, oraz sygnału <tt>s2</tt> od 0.5 do 0.9 z krokiem 0.1. Zaobserwuj związek między położeniem maksimum funkcji korelacji wzajemnej a odległością między centrami gaborów. | ||
| + | |||
| + | |||
| + | * Wykonaj analogiczne iteracje zachowując stałe położenie gaborów (dla obu <tt>t0 = 0.5</tt> zmieniaj natomiast częstość <tt>s2</tt> <math>f</math> od 10 Hz do 16 Hz co 2 Hz. Wymuś stały zakres osi y na -100:100(funkcja <tt>pylab.ylim((-100,100))</tt>) | ||
| + | * | ||
| + | <!-- | ||
| + | import numpy as np | ||
| + | import pylab as py | ||
| + | |||
| + | def gabor(t0=0.5, sigma = 0.1, f = 10, T = 1, Fs = 128, phi =0 ): | ||
| + | |||
| + | dt = 1.0/Fs | ||
| + | t = np.arange(0,T,dt) | ||
| + | s = np.exp( -0.5*((t-t0)/sigma)**2 )*np.cos(2*np.pi*f*t + phi) | ||
| + | return (s,t) | ||
| + | |||
| + | (s1,t) = gabor(t0=0.5,f=10,Fs=1000) | ||
| + | f_corr_t = np.zeros(2*len(t)-1) | ||
| + | f_corr_t[0:len(t)]= -t[len(t)::-1] | ||
| + | f_corr_t[len(t):]=t[1:] | ||
| + | py.figure(1) | ||
| + | for i in range(4): | ||
| + | (s1,t) = gabor(t0=0.5-i*0.1,f=10,Fs=1000) | ||
| + | (s2,t) = gabor(t0=0.5+i*0.1,f=10,Fs=1000) | ||
| + | py.subplot(2,4,i+1) | ||
| + | py.plot(t,s1,t,s2) | ||
| + | |||
| + | py.subplot(2,4,4+(i+1)) | ||
| + | z = np.correlate(s1,s2,mode='full') | ||
| + | py.plot(f_corr_t,z) | ||
| + | py.figure(2) | ||
| + | for i in range(4): | ||
| + | (s1,t) = gabor(t0=0.5,f=10,Fs=1000) | ||
| + | f2 = 10+2*i | ||
| + | (s2,t) = gabor(t0=0.5,f=f2,Fs=1000) | ||
| + | py.subplot(2,4,i+1) | ||
| + | py.plot(t,s1,t,s2) | ||
| + | py.title(f2) | ||
| + | |||
| + | py.subplot(2,4,4+(i+1)) | ||
| + | z = np.correlate(s1,s2,mode='full') | ||
| + | py.plot(f_corr_t,z) | ||
| + | py.ylim((-100,100)) | ||
| + | py.show() | ||
| + | --> | ||
| + | |||
| + | |||
| + | http://localhost:8888/notebooks/Documents/Hoza/WYKLADY/ANALIZA_SYG_WIKI/cwiczenia/AR/Korelacja_i_kowariancja_demo.ipynb | ||
| + | |||
==Wielokanałowe modele AR== | ==Wielokanałowe modele AR== | ||
Model autoregresyjny rozpatrywaliśmy do tej pory jako proces generacji pojedynczego sygnału ''x''. Nic jednak nie stoi na przeszkodzie, aby w chwili czasu ''t'' opisywać wartość nie jednego sygnału, ale jakiejś większej ich liczby, np. ''k''. Możemy wtedy zapisać | Model autoregresyjny rozpatrywaliśmy do tej pory jako proces generacji pojedynczego sygnału ''x''. Nic jednak nie stoi na przeszkodzie, aby w chwili czasu ''t'' opisywać wartość nie jednego sygnału, ale jakiejś większej ich liczby, np. ''k''. Możemy wtedy zapisać | ||
| Linia 18: | Linia 127: | ||
::<math>X(f)=A^{-1}(f) E(f)=H(f) E(f)</math> | ::<math>X(f)=A^{-1}(f) E(f)=H(f) E(f)</math> | ||
| − | ::<math>S(f) = X(f)X^+(f)=H(f)VH^+(f)</math> | + | ::<math>S(f) = X(f)X^+(f)= </math> |
| + | |||
| + | ::::<math>= H(f) E(f) [ H(f) E(f) ]^+ =</math> | ||
| + | |||
| + | ::::<math>= H(f) [E(f)E^+(f)] H^+(f)=</math> | ||
| + | |||
| + | ::::<math>= H(f)VH^+(f)</math> | ||
| + | |||
(symbol <sup>+</sup> oznacza transpozycję połączoną ze sprzężeniem zespolonym elementów macierzy). | (symbol <sup>+</sup> oznacza transpozycję połączoną ze sprzężeniem zespolonym elementów macierzy). | ||
| + | |||
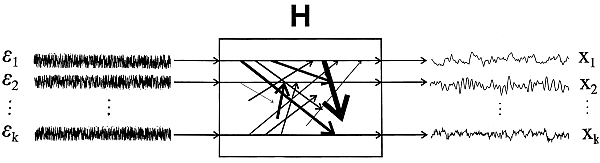
| + | [[Plik:DTF_schemat.png ]] | ||
Macierz ''H'' nazywamy macierzą przejścia modelu (ang. ''transfer matrix''). Widzimy, że transformata Fouriera sygnału powstaje przez pomnożenie macierzy przejścia ''H'' przez transformatę Fouriera szumu ''E'', która teoretycznie nie zależy od częstości. Oznacza to, że własności widmowe opisane współczynnikami modelu (z których wylicza się macierz przejścia) zawarte są w ''H''. | Macierz ''H'' nazywamy macierzą przejścia modelu (ang. ''transfer matrix''). Widzimy, że transformata Fouriera sygnału powstaje przez pomnożenie macierzy przejścia ''H'' przez transformatę Fouriera szumu ''E'', która teoretycznie nie zależy od częstości. Oznacza to, że własności widmowe opisane współczynnikami modelu (z których wylicza się macierz przejścia) zawarte są w ''H''. | ||
| Linia 43: | Linia 161: | ||
Zaobserwuj wielkość wykrytej transmisji między sygnałami 2 a 3 w dwóch sytuacjach: gdy do analizy bierzesz tylko te dwa sygnały (2 i 3) oraz gdy do analizy brane są wszystkie trzy sygnały na raz. Czy możemy zaobserwować różnicę między sytuacją użycia pary sygnałów i informacji z pełnego układu 3-kanałowego? | Zaobserwuj wielkość wykrytej transmisji między sygnałami 2 a 3 w dwóch sytuacjach: gdy do analizy bierzesz tylko te dwa sygnały (2 i 3) oraz gdy do analizy brane są wszystkie trzy sygnały na raz. Czy możemy zaobserwować różnicę między sytuacją użycia pary sygnałów i informacji z pełnego układu 3-kanałowego? | ||
| − | |||
[[Analiza_sygnałów_-_ćwiczenia]]/AR_2 | [[Analiza_sygnałów_-_ćwiczenia]]/AR_2 | ||
Aktualna wersja na dzień 12:45, 23 sty 2018
Spis treści
Korelacja i funkcja korelacji
Dla przypomnienia: zagadnienia te poruszane były na wykładzie
Kowariancja:
- [math]\sigma _{xy} = \int {(x(t)-\bar{x}) (y(t)-\bar{y}) dt }[/math]
Kowariancja dwóch zmiennych losowych jest miarą tego na ile dwie zmienne losowe mają podobne tendencje do zmian. Przykład: w zmiennej x parami podajemy wartość pierwszej i drugiej zmiennej
x = np.array([[0, 2], [1, 1], [2, 0]]).T
W tej postaci łatwo zauważyć, że gdy pierwsza zmienna rośnie to druga maleje:
>>> x
array([[0, 1, 2],
[2, 1, 0]])
Tę własność naszych zmiennych wyrażają elementy pozadiagonalne macierzy kowariancji:
>>> np.cov(x)
array([[ 1., -1.],
[-1., 1.]])
Współczynnik normalizacyjny:
- [math]\sigma _{ss} = \int {\left(s(t)-\bar{s}\right)^2 dt}[/math]
Implementacja w Pythonie: numpy.cov
Korelacja
- [math]\rho _{xy}= \frac{\sigma _{xy}}{\sqrt{\sigma _{xx} \sigma _{yy}}}[/math]
Implementacja w Pythonie: numpy.corrcoef
Badanie zależności między sygnałami przy pomocy funkcji korelacji
def gabor(t0=0.5, sigma = 0.1, f = 10, T = 1, Fs = 128, phi =0 ):
dt = 1.0/Fs
t = np.arange(0,T,dt)
s = np.exp( -0.5*((t-t0)/sigma)**2 )*np.cos(2*np.pi*f*t + phi)
return (s,t)
- wygeneruj dwa sygnały długości [math]T=2s[/math] próbkowane z częstością [math]f_s=128[/math] Hz przy uzyciu funkcji gabor. Oba gabory mają częstość [math]f=10[/math] Hz i [math]\sigma =0.1[/math] s. Oba sygnały s1 i s2 są centrowane na [math]t_0=0.5[/math] s
- oblicz funkcję korelacji wzajemnej z = np.correlate(s1,s2,mode='full')
- Jaka jest długość sygnału z?
- Wykreśl w funkcji odpowiednich skal czasu na dwóch subplotach: na górnym sygnały s1 i s2 a na dolnym z.
- Zaobserwuj położenie maksimum funkcji korelacji wzajemnej. Jaki jest związek oscylacji w funkcji korelacji wzajemnej z oscylacjami funkcji s1 i s2
Wskazówka: Związek między czasem t dla sygnałów s1 i s2 a skalą czasu dla korelacji f_corr_t można zapisać w Pythonie:
f_corr_t = np.zeros(2*len(t)-1)
f_corr_t[0:len(t)]= -t[len(t)::-1]
f_corr_t[len(t):]=t[1:]
- Powtórz punkty 1-5 zmieniając położenie sygnału s1 od 0.5 do 0.1 z krokiem 0.1, oraz sygnału s2 od 0.5 do 0.9 z krokiem 0.1. Zaobserwuj związek między położeniem maksimum funkcji korelacji wzajemnej a odległością między centrami gaborów.
- Wykonaj analogiczne iteracje zachowując stałe położenie gaborów (dla obu t0 = 0.5 zmieniaj natomiast częstość s2 [math]f[/math] od 10 Hz do 16 Hz co 2 Hz. Wymuś stały zakres osi y na -100:100(funkcja pylab.ylim((-100,100)))
*
Wielokanałowe modele AR
Model autoregresyjny rozpatrywaliśmy do tej pory jako proces generacji pojedynczego sygnału x. Nic jednak nie stoi na przeszkodzie, aby w chwili czasu t opisywać wartość nie jednego sygnału, ale jakiejś większej ich liczby, np. k. Możemy wtedy zapisać wzór modelu k-kanałowego jako
- [math]X(t) = \sum _{i=1}^p A(i) X(t-i) +E(t)[/math]
gdzie X(t) i E(t) są wektorami odpowiednio — wartości wszystkich opisywanych modelem sygnałów (x1, x2, ..., xk) w chwili czasu t i wartości k niezależnych procesów czysto losowych (ϵ1, ϵ2, ..., ϵk) w chwili czasu t:
- [math]X(t)=\left(\begin{array}{l} x_1(t)\\x_2(t)\\\vdots\\x_k(t) \end{array} \right)\ \ \ E(t)=\left(\begin{array}{l} \epsilon_1(t)\\ \epsilon_2(t)\\\vdots\\ \epsilon_k(t) \end{array} \right)[/math]
Proces opisujący jednocześnie więcej niż jeden sygnał nazywamy wielokanałowym lub wielozmiennym (ang. multichannel, multivariate). Zauważmy, że (jeden) model wielokanałowy nie jest prostym powieleniem kilku modeli jednokanałowych. Tutaj współczynniki A są macierzami rozmiaru k×k, zawierającymi oprócz zależności osobno dla każdego z sygnałów (kanałów modelu) również wyrazy pozadiagonalne, opisujące zależności między sygnałami składowymi.
Wzory opisujące model w dziedzinie częstości, w szczególności wzór na transformację Fouriera sygnału X oraz na widmo S (czyli funkcję gęstości widmowej mocy) wyglądają identycznie jak w przypadku jednokanałowym z tym, że odpowiednie wielkości (A, H, S) są teraz macierzami rozmiaru k×k, natomiast X(f) i E(f) są wektorami o rozmiarze k:
- [math]A(f)X(f) =E(f)[/math]
- [math]X(f)=A^{-1}(f) E(f)=H(f) E(f)[/math]
- [math]S(f) = X(f)X^+(f)= [/math]
- [math]= H(f) E(f) [ H(f) E(f) ]^+ =[/math]
- [math]= H(f) [E(f)E^+(f)] H^+(f)=[/math]
- [math]= H(f)VH^+(f)[/math]
(symbol + oznacza transpozycję połączoną ze sprzężeniem zespolonym elementów macierzy).
Macierz H nazywamy macierzą przejścia modelu (ang. transfer matrix). Widzimy, że transformata Fouriera sygnału powstaje przez pomnożenie macierzy przejścia H przez transformatę Fouriera szumu E, która teoretycznie nie zależy od częstości. Oznacza to, że własności widmowe opisane współczynnikami modelu (z których wylicza się macierz przejścia) zawarte są w H.
Widmo S procesu wielokanałowego jest również macierzą rozmiaru k×k. Na przekątnej zawiera ona tzw. widma własne (ang. autospectra), a poza przekątną widma wzajemne (ang. cross-spectra) mówiące o wspólnych dla danej pary kanałów składowych w częstości.
Ponieważ macierz H zawiera w sobie związki między wszystkimi sygnałami wchodzącymi w skład opisywanego układu oraz jest ona niesymetryczna, może posłużyć do skonstruowania funkcji opisującej zależności pomiędzy sygnałami. Funkcją taką jest na przykład kierunkowa funkcja przejścia (ang. directed transfer function, DTF) opisana w wersji znormalizowanej wzorem.
- [math]\gamma_{ij}(f)=\frac{\left|H_{ij}(f)\right|^2}{\sum_{m=1}^{k}\left|H_{im}(f)\right|^2}[/math]
Opisuje ona stosunek wpływu w częstości f sygnału transmitowanego z kanału j do kanału i w danym zestawie w stosunku do wszystkich wpływów transmitowanych w tej częstości do kanału i. Dzięki temu jest ona znormalizowana: jej wartości zawierają się w przedziale [0, 1]; wartość 0 oznacza brak transmisji z kanału j do kanału i, wartość bliska 1 oznacza silny przepływ sygnału w tym kierunku.
Ćwiczenia
Aby zapoznać się z działaniem funkcji DTF możemy użyć wtyczki DTF do programu Svarog. Oblicza ona znormalizowaną funkcję DTF dla wybranego zestawu kanałów wczytanych z pliku i wybranego rzędu modelu.
Sygnał testowy 1 (dane_dtf_1.bin, dane_dtf_1.xml) jest to układ 3-kanałowy, w którym kanały 1 i 3 pochodzą z zapisu EEG ludzkiego z czaszki, pierwszy z przodu głowy, drugi z tyłu głowy, kanał 2 jest zaś szumem o rozkładzie normalnym. Sygnał zbierany był w trakcie czuwania z zamkniętymi oczami, oczekujemy więc silnej składowej w paśmie alfa (8-12 Hz), która, jak jest to wiadomo, jest generowana z tyłu głowy. Jak zinterpretujesz otrzymany wynik?
*
Sygnał testowy 2 (dane_dtf_2.bin, dane_dtf_2.xml) jest to również układ 3-kanałowy, demonstrujący tzw. problem wspólnego źródła. Sygnał 1 pochodzi z rejestracji ludzkiego EEG podczas czuwania z zamkniętymi oczami, sygnał 2 to częściowo ten sam sygnał opóźniony o jedną próbkę z dodanym szumem, a sygnał 3 to sygnał 1 opóźniony o dwie próbki i z dodanym (innym) szumem. Ponieważ sygnały 2 i 3 są opóźnionymi wersjami sygnału 1 oczekujemy wykrycia transmisji 1→2 i 1→3. Pytanie jest czy powinniśmy oczekiwać transmisji 2→3? W końcu w kanale 3 jest sygnał podobny do sygnału z kanału 2 i na dodatek opóźniony w stosunku do niego o 1 próbkę.
Zaobserwuj wielkość wykrytej transmisji między sygnałami 2 a 3 w dwóch sytuacjach: gdy do analizy bierzesz tylko te dwa sygnały (2 i 3) oraz gdy do analizy brane są wszystkie trzy sygnały na raz. Czy możemy zaobserwować różnicę między sytuacją użycia pary sygnałów i informacji z pełnego układu 3-kanałowego?