Ćwiczenia 6: Różnice pomiędzy wersjami
| (Nie pokazano 28 pośrednich wersji utworzonych przez tego samego użytkownika) | |||
| Linia 11: | Linia 11: | ||
** w dziedzinie czasu to mnożenie odpowiada splotowi sygnału z pewną funkcją tzw.funkcją odpowiedzi impulsowej | ** w dziedzinie czasu to mnożenie odpowiada splotowi sygnału z pewną funkcją tzw.funkcją odpowiedzi impulsowej | ||
| − | + | =Filtry cyfrowe: powtórka z wykładu= | |
| − | == | + | ==Działanie filtra w dziedzinie czasu== |
Najczęściej, wyjście filtra jest kombinacją liniową: | Najczęściej, wyjście filtra jest kombinacją liniową: | ||
| − | :<math> y[n] = b(1)x[n] | + | :<math> y[n] = b(1)x[n] + b(2)x[n-1] + ... + b(n_b+1)x[n-n_b]</math> |
:::<math> - a(2)y[n-1] - ... - a(n_a+1)y[n-n_a] </math> | :::<math> - a(2)y[n-1] - ... - a(n_a+1)y[n-n_a] </math> | ||
| Linia 27: | Linia 27: | ||
Większa z liczb <math> n_b </math> i <math> n_a </math> określa '''rząd''' filtra. | Większa z liczb <math> n_b </math> i <math> n_a </math> określa '''rząd''' filtra. | ||
| − | + | Zauważmy, że matematycznie operacje te odpowiadają splataniiu próbek wejściowych z wektorem <math>b</math> i próbek wyjściowych z wektorem <math>a</math>. | |
| + | |||
| + | ==Nazewnictwo== | ||
* Jeśli <math>n_a=0 </math> i <math>n_b \ne 0 </math> filtr nazywany jest filtrem o skończonej odpowiedzi impulsowej (FIR), czasem jest on nazywany średnią ruchomą (MA). | * Jeśli <math>n_a=0 </math> i <math>n_b \ne 0 </math> filtr nazywany jest filtrem o skończonej odpowiedzi impulsowej (FIR), czasem jest on nazywany średnią ruchomą (MA). | ||
| Linia 59: | Linia 61: | ||
===Opóźnienie grupowe=== | ===Opóźnienie grupowe=== | ||
| − | Pokazaliśmy, że filtr mnoży każdą składową przez liczbę | + | Pokazaliśmy, że filtr mnoży każdą składową przez liczbę <math>M(f)e^{i \phi(f)}</math>, przez co zmienia jej fazę o <math>\phi(f)</math>. W konsekwencji składowa o częstości <math>f</math> pojawia się na wyjściu filtra z opóźnieniem: |
| − | + | <math>\tau_g(f)=-\frac{d \phi(f)}{d f}</math> | |
| + | |||
| + | * Jeśli zależność fazy od częstości jest liniowa (tak jest dla filtrów FIR) to <math>\tau_g(f)=const</math>, czyli wszystkie składowe pojawiają się z tym samym opóźnieniem. | ||
| + | * Dla nieliniowej zależności <math>\phi(f)</math> każda składowa jest opóźniona inaczej. Powoduje to dodatkowe zniekształcenia sygnału. | ||
| + | |||
| + | =====Opóźnienie grupowe i fazowe filtru - interpretacja===== | ||
| + | |||
| + | Interpretacja własności fazowych filtru łatwiejsza jest jeśli zamiast fazy wykreślimy opóźnienie fazowe lub grupowe. | ||
| + | * Opóźnienie fazowe zdefiniowane jest jako: | ||
| + | |||
| + | ::<math>\tau_p(\omega )=-\frac{\phi(\omega)}{\omega}</math> | ||
| + | |||
| + | Sens tej definicji widać jeśli zastosujemy ją do sinusa o częstości <math>\omega_1</math> i fazie <math>\phi_1</math>. | ||
| + | <math>\sin(\omega_1 t + \phi_1)= \sin(\omega_1 t - \omega_1 \tau_p(\omega_1)) = \sin(\omega_1 (t-\tau_p(\omega_1))) </math> | ||
| + | |||
| + | |||
| + | * opóźnienie grupowe zdefiniowane jest jako: | ||
| + | |||
| + | ::<math>\tau _g(\omega )=-\frac{d \phi (\omega )}{d \omega }</math> | ||
| + | |||
| + | Sens tej definicji widać jeśli rozważymy co stanie się z sygnałem składającym się z dwóch cosinusiod o bliskich sobie częstościach <math>\omega_1</math> i <math> \omega_2</math>. Załóżmy, że filtr przenosi każdą z nich z niezmienioną amplitudą i jedynie faza ulega przesunięciu odpowiednio o <math>\phi_1</math> i <math>\phi_2</math>. | ||
| + | Na wejściu nasz sygnał można przedstawić tak: | ||
| + | :<math>\cos(\omega_1 t) + \cos(\omega_2 t) = 2\cos\left(\frac{\omega_1-\omega_2}{2}t\right)\cos\left(\frac{\omega_1+\omega_2}{2}t\right)= 2\cos\left(\frac{\Delta\omega}{2}t\right)\cos\left(\frac{\omega_1+\omega_2}{2}t\right)</math> | ||
| + | Widać, że takie dwa cosinusy powodują efekt dudnienia. Innymi słowy można je postrzegać jako oscylację z częstością średnią obu cosinusów modulowaną wolno zmienną (<math>\Delta \omega/2</math>) obwiednią. | ||
| + | Sygnał wyjściowy z naszego filtru modyfikującego tylko fazy można zapisać tak: | ||
| + | :<math>y = \cos(\omega_1 t +\phi_1) + \cos(\omega_2 t +\phi_2) = 2\cos\left(\frac{\omega_1-\omega_2}{2}t +\frac{\phi_1-\phi_2}{2}\right)\cos\left(\frac{\omega_1+\omega_2}{2}t+\frac{\phi_1+\phi_2}{2}\right)</math> | ||
| + | Oznaczmy <math>\Delta \phi = \phi_1 - \phi_2</math>. | ||
| + | :<math> y = 2\cos\left(\frac{1}{2} \left(\Delta\omega t +\Delta\phi \right) \right)\cos\left(\frac{\omega_1+\omega_2}{2}t+\frac{\phi_1+\phi_2}{2}\right) </math> | ||
| − | \ | + | Wprowadzając <math> t_g = - \frac{ \Delta \phi}{\Delta \omega}</math> mamy: |
| − | \ | + | :<math> |
| − | \ | + | y = 2\cos\left(\frac{1}{2} \left(\Delta\omega t - \Delta\omega t_g \right) \right)\cos\left(\frac{\omega_1+\omega_2}{2}t+\frac{\phi_1+\phi_2}{2}\right) = |
| − | \ | + | </math> |
| − | } | + | :<math> |
| + | = 2\cos\left(\frac{1}{2} \Delta\omega \left(t - t_g \right) \right)\cos\left(\frac{\omega_1+\omega_2}{2}t+\frac{\phi_1+\phi_2}{2}\right) | ||
| + | </math> | ||
| + | Zatem widzimy, że obwiednia przesunięta jest w czasie o <math>t_g</math>. W granicznym przypadku ciągłym <math>\lim_{\Delta \omega \to 0}t_g = \tau_g</math> | ||
===Filtrowanie z zerowym przesunięciem fazowym=== | ===Filtrowanie z zerowym przesunięciem fazowym=== | ||
Można temu zaradzić następującą procedurą: | Można temu zaradzić następującą procedurą: | ||
| − | + | ||
| − | + | * filtrujemy sygnał <math>x[0], \dots , x[n] \rightarrow y[0],\dots, y[n]</math> wprowadzamy przesunięcie fazy o <math>\phi(f)</math> | |
| − | + | * odwracamy kolejność próbek i ponownie filtrujemy <math> y[n],\dots,y[0] \rightarrow y'[n],\dots,y'[0] </math> wprowadzamy przesunięcie fazy o <math>-\phi(f)</math> | |
| − | + | * odwracamy kolejność próbek: <math>y'[0],\dots,y'[n] </math> | |
| − | |||
Efektywnie wygląda to tak jakbyśmy przefiltrowali sygnał filtrem o funkcji przenoszenia z zerowym przesunięciem fazowym: | Efektywnie wygląda to tak jakbyśmy przefiltrowali sygnał filtrem o funkcji przenoszenia z zerowym przesunięciem fazowym: | ||
| − | + | <math>H_{eff}(f)=A(f)e^{i \phi(f)}\cdot A(f)e^{-i \phi(f)}= A(f)^2</math> | |
| − | === | + | ===Pytanie=== |
| − | + | * co to jest odpowiedź impulsowa filtra? | |
| + | * jak filtr działa w dziedzinie czasu? | ||
| + | * co to jest funkcja przenoszenia filtra? | ||
| + | * jak filtr działa w dziedzinie częstości? | ||
| − | + | =Klasyczne filtry IIR= | |
| − | + | Mamy cztery klasyczne typy filtrów IIR: | |
| − | + | ;Butterwortha: daje monotoniczną funkcję przenoszenia | |
| − | + | ;Czebyszewa typu I: - dopuszczalne tętnienia w paśmie przenoszenia, monotoniczne w paśmie zaporowym | |
| − | + | ;Czebyszewa typu II:-monotoniczne w paśmie przenoszenia, dopuszczalne tętnienia w paśmie zaporowym, nieco mniej strome zbocze opadające funkcji przenoszenia niż dla typu I | |
| − | + | ;Filtr eliptyczny: mają dopuszczalne tętnienia zarówno w paśmie przenoszenia jak i tłumienia. Dają najbardziej strome zbocza przy tym samym rzędzie co powyższe wersje. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
===Specyfikacja filtra=== | ===Specyfikacja filtra=== | ||
| − | + | W określaniu parametrów filtrów używa się często pojęcia decybel [dB]. | |
| − | + | Dwa poziomy sygnału <math>P</math> oraz <math>P_0</math> różnią się o <math>n</math> decybeli, jeżeli | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | \ | + | ::<math>n = 10 \log _{10} \frac{P}{P_0} = 10 \log_{10}\left(\frac{A}{A_0}\right)^2 = 20\log_{10}\frac{A}{A_0} </math> |
| − | |||
| − | + | * Ilustracja pojęć używanych przy specyfikacji filtra: | |
| − | + | ** Rp- tętnienia w paśmie przenoszenia | |
| − | + | ** Rs - tłumienie w paśmie tłumienia | |
| + | |||
| + | [[Plik:Filtry.png|600px|thumb|center| Przykładowe parametry specyfikujące filter ]] | ||
| + | |||
| + | * można też podać częstość odcięcia i zbocze filtru zgodnie z oznaczeniami na poniższym rysunku: | ||
| + | [[Plik:Butterworth_filter_bode_plot.png|600px|center ]] | ||
| + | |||
| + | * Przykład projektu fltra i jego działanie na sygnały testowe: | ||
| + | |||
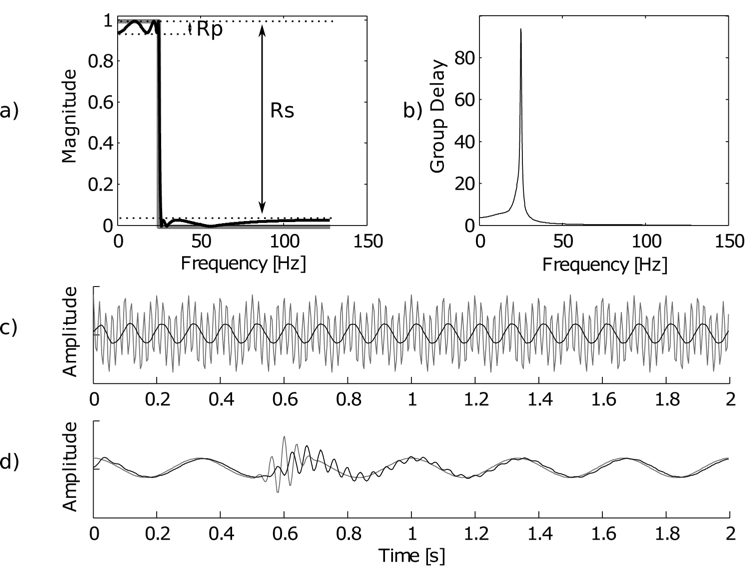
| + | [[Plik:Fig_2_1.png|center| thumb|750px| a) Moduł funkcji przenoszenia. Projekt (szara linia), realizacja dla filtra eliptycznego 5 rzędu (czarna linia), b) Opóźnienie grupowe. c) Zastosowanie filtra do sygnału złożonego z sinusoidy 10Hz i 50Hz: szare - wejście, czarne- wyjście. d) Przesunięcia i efekty brzegowe: wejście (szare) to sinusoida 3Hz ze strukturą 25Hz w okolicach 0.6s; wyjście (czarna linia) (i) w pierwszych 0.1s zniekształcenia brzegowe (ii)opóźnienia: sinusoida 3Hz jest opóźniona wzg wejścia, struktura 25Hz ma większe opóźnienie i rozciągłość, co wynika z funkcji opóźnienia grupowego b)} } ]] | ||
| + | |||
| + | ==Projektowanie filtrów w programie Svarog== | ||
| + | |||
| + | Program SVAROG ma wygodne narzędzie do projektowania filtrów IIR. Zanim przejdziemy do implementowania tych filtrów w pythonie, spróbujemy nabrać wyczucia w SVAROGU. | ||
| + | |||
| + | W celu zaprojektowania filtru w Svarogu należy sprecyzować następujące parametry: | ||
| + | |||
| + | * '''Typ filtru''' - dolnoprzepustowy, górnoprzepustowy, pasmowoprzepustowy, pasmowozaporowy. | ||
| + | * '''Rodzaj filtru''' - Butterwortha, Czebyszewa I i II, eliptyczny. | ||
| + | * '''Częstotliwość graniczna pasma przepustowego 1''' - górna częstotliwość pasma przenoszenia oddzielająca pasmo przenoszenia od obszaru przejściowego. | ||
| + | * '''Częstotliwość graniczna pasma przepustowego 2''' - w przypadku filtru pasmowoprzepustowego lub pasmowozaporowego istnieją dwa obszary przejściowego; w związku z tym częstotliwość graniczna 1 oddziela pasmo przenoszenia od pierwszego obszaru przejściowego (ma niższą wartość), a częstotliwość graniczna 2 separuje pasmo przenoszenia od drugiego obszaru przejściowego. | ||
| + | * '''Częstotliwość graniczna pasma zaporowego 1''' - dolna częstotliwość pasma zaporowego oddzielająca pasmo zaporowe od obszaru przejściowego. | ||
| + | * '''Częstotliwość graniczna pasma zaporowego 2''' - w przypadku filtru pasmowoprzepustowego lub pasmowozaporowego częstotliwość graniczna 1 oddziela pasmo zaporowe od pierwszego obszaru przejściowego (ma niższą wartość), a częstotliwość graniczna 2 separuje pasmo zaporowe od drugiego obszaru przejściowego. | ||
| + | * '''Zafalowania w paśmie przenoszenia''' - maksymalna wartość tłumienia w paśmie przenoszenia. | ||
| + | * '''Tłumienie w paśmie zaporowym''' - minimalna wartość tłumienia w paśmie zaporowym. | ||
| + | |||
| + | ===Przykład=== | ||
| + | Rysunek poniżej przedstawia charakterystykę amplitudową górnoprzepustowego filtru Czebyszewa I. Filtr został zaprojektowany przy użyciu następujących parametrów: | ||
| + | |||
| + | * Filter type = high-pass | ||
| + | * Filter family = Chebyshev I | ||
| + | * Passband edge frequency 1 = 20 Hz | ||
| + | * Stopband edge frequency 1 = 16 Hz | ||
| + | * Passband ripple = 3 dB | ||
| + | * Stopband attenuation = 40 dB | ||
| + | |||
| + | Rząd filtru zostaje dostosowany do wymagań projektowych. | ||
| + | |||
| + | [[Plik:Svarog_fillter_bands.png|center|800px|thumb|<figure id="uid3"/>Charakterystyka amplitudowa górnoprzepustowego filtru Czebyszewa I.]] | ||
| + | |||
| + | [[Plik:Projekt filtra svarog.png |center| thumb|750px| Okienko projektowania flirtrów w programie SVAROG]] | ||
| + | |||
| + | ===Zadanie=== | ||
| + | |||
| + | Przydadzą nam się pliki: | ||
| + | [https://drive.google.com/open?id=0BzwQ_Lscn8yDNGc0aU5jSDFFMmc Plik z sygnałem EKG] | ||
| + | [https://drive.google.com/open?id=0BzwQ_Lscn8yDOF9jX0pjcG9LSGc Plik z metadanymi do tego sygnału] | ||
| + | |||
| + | |||
| + | |||
| + | <!-- | ||
=Filtrowanie a sploty= | =Filtrowanie a sploty= | ||
| Linia 232: | Linia 296: | ||
'''Zera i bieguny''' filtra to odpowiednio miejsca zerowe licznika i mianownika funkcji przenoszenia. | '''Zera i bieguny''' filtra to odpowiednio miejsca zerowe licznika i mianownika funkcji przenoszenia. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
--> | --> | ||
| − | |||
| − | |||
| − | |||
[[Analiza_sygnałów_-_ćwiczenia]]/Filtry | [[Analiza_sygnałów_-_ćwiczenia]]/Filtry | ||
Aktualna wersja na dzień 11:26, 20 sty 2021
Analiza_sygnałów_-_ćwiczenia/Filtry
Wprowadzenie
- W analizie sygnałów filtowanie rozumiane jest najczęściej jako operacja mająca na celu usunięcie z sygnału pewnych składowych. Często operacja ta dotyczy składowych charakteryzowanych przez częstości np.:
- w sygnale EEG wiemy, że znaczącym artefaktem jest sygnał pochodzący od sieci energetycznej, zatem stosujemy filtr usuwający składową około 50Hz (w Europie).
- inny przykład z tej samej dziedziny: interesuje nas czynność alfa (8 -12 Hz), chcemy zatem usunąć z sygnału składowe o niższych i o wyższych częstościach.
- Filtry często są realizowane w postaci systemów LTI (linear time invariant):
- dla takich systemów funkcjami własnymi są zespolone eksponensy (czyli na mocy wzorów Eulera: sinusy i cosinusy)
- w przestrzeni częstości filtrowanie odpowiada przemnożeniu każdej składowej częstościowej przez pewną liczbę (zespoloną)-> zatem zmienić się może amplituda i faza każdej częstości
- w dziedzinie czasu to mnożenie odpowiada splotowi sygnału z pewną funkcją tzw.funkcją odpowiedzi impulsowej
Filtry cyfrowe: powtórka z wykładu
Działanie filtra w dziedzinie czasu
Najczęściej, wyjście filtra jest kombinacją liniową:
- [math] y[n] = b(1)x[n] + b(2)x[n-1] + ... + b(n_b+1)x[n-n_b][/math]
- [math] - a(2)y[n-1] - ... - a(n_a+1)y[n-n_a] [/math]
gdzie:
- [math] n_b [/math] liczba przeszłych próbek wejściowych [math] x [/math]
- [math] n_a [/math] liczba przeszłych próbek wyjściowych [math] y [/math]
użytych do obliczenia aktualnego wyjścia [math] y[n] [/math].
Większa z liczb [math] n_b [/math] i [math] n_a [/math] określa rząd filtra.
Zauważmy, że matematycznie operacje te odpowiadają splataniiu próbek wejściowych z wektorem [math]b[/math] i próbek wyjściowych z wektorem [math]a[/math].
Nazewnictwo
- Jeśli [math]n_a=0 [/math] i [math]n_b \ne 0 [/math] filtr nazywany jest filtrem o skończonej odpowiedzi impulsowej (FIR), czasem jest on nazywany średnią ruchomą (MA).
- Jeśli [math]n_b=0 [/math] i [math]n_a \ne 0 [/math] filtr ma nieskończoną odpowiedź impulsową (IIR). Bywa też nazywany filtrem autoregresyjnym (AR).
- Jeśli [math]n_b \ne 0 [/math] i [math]n_a \ne 0 [/math] także jest filtrem o nieskończonej odpowiedzi impulsowej. Czasem mówi się o nim filtr ARMA - autoregressive moving average.
Zwykle filtry IIR mają niższy rząd niż filtry FIR o tym samym poziomie tłumienia.
Przejście do dziedziny częstości
- [math] y[n]+ a(2)y[n-1] + ... + a(n_a+1)y[n-n_a] = [/math]
- [math] =b(1)x[n] + b(2)x[n-1] + ... + b(n_b+1)x[n-n_b] [/math]
- [math] y[n]+ a(2)y[n-1] + ... + a(n_a+1)y[n-n_a] = [/math]
zastosowanie transformaty Z do bu stron daje:
- [math]A(z)Y(z)=B(z)X(z)[/math]
Przekształcamy:
- [math]Y(z)=A(z)^{-1}B(z)X(z) =H(z)X(z)[/math]
Funkcja[math]H$[/math] w tym równaniu nazywana jest funkcją przenoszenia filtra. Ma ona formę ilorazu dwóch wielomianów:
- [math]H(z)=\frac{b(1)+b(2)z^{-1}+\dots+b(n_b+1)z^{-n_b}}{a(1)+a(2)z^{-1}+\dots+a(n_a+1)z^{-n_a}}[/math]
Działanie filtra w dziedzinie częstości
- Funkcję przenoszenia zależną od częstości, [math]H(f)[/math], można uzyskać podstawiając [math] z=e^{i 2 \pi f}[/math]
- Ta funkcja przypisuje każdej częstości [math]f[/math] pewną liczbę zespoloną, która ma moduł [math]M[/math] i fazę[math]\phi[/math]:
- [math]H(f)=M(f)e^{i \phi(f)}[/math]
- Zatem działanie filtra to mnożenie każdej składowej Fourierowskiej sygnału przez liczbę zespoloną [math]H(f)[/math];
- Widać więc, że filtr może takiej składowej zmienić amplitudę i fazę, ale nie może jej zmienić częstości.
- Jest to przejaw tego, że sinusoidy są funkcjami własnymi układów LTI
Opóźnienie grupowe
Pokazaliśmy, że filtr mnoży każdą składową przez liczbę [math]M(f)e^{i \phi(f)}[/math], przez co zmienia jej fazę o [math]\phi(f)[/math]. W konsekwencji składowa o częstości [math]f[/math] pojawia się na wyjściu filtra z opóźnieniem: [math]\tau_g(f)=-\frac{d \phi(f)}{d f}[/math]
- Jeśli zależność fazy od częstości jest liniowa (tak jest dla filtrów FIR) to [math]\tau_g(f)=const[/math], czyli wszystkie składowe pojawiają się z tym samym opóźnieniem.
- Dla nieliniowej zależności [math]\phi(f)[/math] każda składowa jest opóźniona inaczej. Powoduje to dodatkowe zniekształcenia sygnału.
Opóźnienie grupowe i fazowe filtru - interpretacja
Interpretacja własności fazowych filtru łatwiejsza jest jeśli zamiast fazy wykreślimy opóźnienie fazowe lub grupowe.
- Opóźnienie fazowe zdefiniowane jest jako:
- [math]\tau_p(\omega )=-\frac{\phi(\omega)}{\omega}[/math]
Sens tej definicji widać jeśli zastosujemy ją do sinusa o częstości [math]\omega_1[/math] i fazie [math]\phi_1[/math]. [math]\sin(\omega_1 t + \phi_1)= \sin(\omega_1 t - \omega_1 \tau_p(\omega_1)) = \sin(\omega_1 (t-\tau_p(\omega_1))) [/math]
- opóźnienie grupowe zdefiniowane jest jako:
- [math]\tau _g(\omega )=-\frac{d \phi (\omega )}{d \omega }[/math]
Sens tej definicji widać jeśli rozważymy co stanie się z sygnałem składającym się z dwóch cosinusiod o bliskich sobie częstościach [math]\omega_1[/math] i [math] \omega_2[/math]. Załóżmy, że filtr przenosi każdą z nich z niezmienioną amplitudą i jedynie faza ulega przesunięciu odpowiednio o [math]\phi_1[/math] i [math]\phi_2[/math]. Na wejściu nasz sygnał można przedstawić tak:
- [math]\cos(\omega_1 t) + \cos(\omega_2 t) = 2\cos\left(\frac{\omega_1-\omega_2}{2}t\right)\cos\left(\frac{\omega_1+\omega_2}{2}t\right)= 2\cos\left(\frac{\Delta\omega}{2}t\right)\cos\left(\frac{\omega_1+\omega_2}{2}t\right)[/math]
Widać, że takie dwa cosinusy powodują efekt dudnienia. Innymi słowy można je postrzegać jako oscylację z częstością średnią obu cosinusów modulowaną wolno zmienną ([math]\Delta \omega/2[/math]) obwiednią. Sygnał wyjściowy z naszego filtru modyfikującego tylko fazy można zapisać tak:
- [math]y = \cos(\omega_1 t +\phi_1) + \cos(\omega_2 t +\phi_2) = 2\cos\left(\frac{\omega_1-\omega_2}{2}t +\frac{\phi_1-\phi_2}{2}\right)\cos\left(\frac{\omega_1+\omega_2}{2}t+\frac{\phi_1+\phi_2}{2}\right)[/math]
Oznaczmy [math]\Delta \phi = \phi_1 - \phi_2[/math].
- [math] y = 2\cos\left(\frac{1}{2} \left(\Delta\omega t +\Delta\phi \right) \right)\cos\left(\frac{\omega_1+\omega_2}{2}t+\frac{\phi_1+\phi_2}{2}\right) [/math]
Wprowadzając [math] t_g = - \frac{ \Delta \phi}{\Delta \omega}[/math] mamy:
- [math] y = 2\cos\left(\frac{1}{2} \left(\Delta\omega t - \Delta\omega t_g \right) \right)\cos\left(\frac{\omega_1+\omega_2}{2}t+\frac{\phi_1+\phi_2}{2}\right) = [/math]
- [math] = 2\cos\left(\frac{1}{2} \Delta\omega \left(t - t_g \right) \right)\cos\left(\frac{\omega_1+\omega_2}{2}t+\frac{\phi_1+\phi_2}{2}\right) [/math]
Zatem widzimy, że obwiednia przesunięta jest w czasie o [math]t_g[/math]. W granicznym przypadku ciągłym [math]\lim_{\Delta \omega \to 0}t_g = \tau_g[/math]
Filtrowanie z zerowym przesunięciem fazowym
Można temu zaradzić następującą procedurą:
- filtrujemy sygnał [math]x[0], \dots , x[n] \rightarrow y[0],\dots, y[n][/math] wprowadzamy przesunięcie fazy o [math]\phi(f)[/math]
- odwracamy kolejność próbek i ponownie filtrujemy [math] y[n],\dots,y[0] \rightarrow y'[n],\dots,y'[0] [/math] wprowadzamy przesunięcie fazy o [math]-\phi(f)[/math]
- odwracamy kolejność próbek: [math]y'[0],\dots,y'[n] [/math]
Efektywnie wygląda to tak jakbyśmy przefiltrowali sygnał filtrem o funkcji przenoszenia z zerowym przesunięciem fazowym: [math]H_{eff}(f)=A(f)e^{i \phi(f)}\cdot A(f)e^{-i \phi(f)}= A(f)^2[/math]
Pytanie
- co to jest odpowiedź impulsowa filtra?
- jak filtr działa w dziedzinie czasu?
- co to jest funkcja przenoszenia filtra?
- jak filtr działa w dziedzinie częstości?
Klasyczne filtry IIR
Mamy cztery klasyczne typy filtrów IIR:
- Butterwortha
- daje monotoniczną funkcję przenoszenia
- Czebyszewa typu I
- - dopuszczalne tętnienia w paśmie przenoszenia, monotoniczne w paśmie zaporowym
- Czebyszewa typu II
- -monotoniczne w paśmie przenoszenia, dopuszczalne tętnienia w paśmie zaporowym, nieco mniej strome zbocze opadające funkcji przenoszenia niż dla typu I
- Filtr eliptyczny
- mają dopuszczalne tętnienia zarówno w paśmie przenoszenia jak i tłumienia. Dają najbardziej strome zbocza przy tym samym rzędzie co powyższe wersje.
Specyfikacja filtra
W określaniu parametrów filtrów używa się często pojęcia decybel [dB]. Dwa poziomy sygnału [math]P[/math] oraz [math]P_0[/math] różnią się o [math]n[/math] decybeli, jeżeli
- [math]n = 10 \log _{10} \frac{P}{P_0} = 10 \log_{10}\left(\frac{A}{A_0}\right)^2 = 20\log_{10}\frac{A}{A_0} [/math]
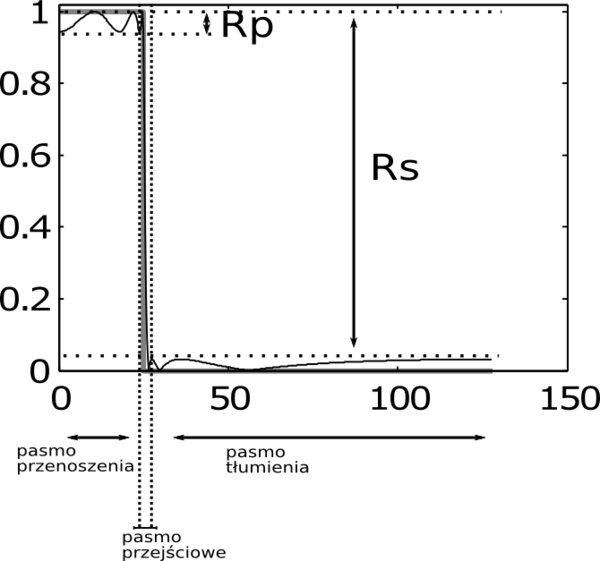
- Ilustracja pojęć używanych przy specyfikacji filtra:
- Rp- tętnienia w paśmie przenoszenia
- Rs - tłumienie w paśmie tłumienia
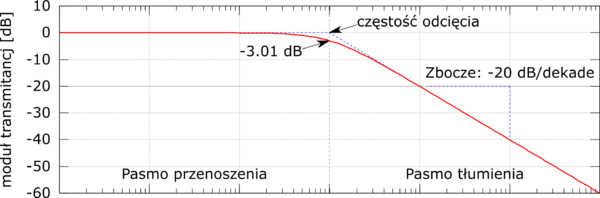
- można też podać częstość odcięcia i zbocze filtru zgodnie z oznaczeniami na poniższym rysunku:
- Przykład projektu fltra i jego działanie na sygnały testowe:
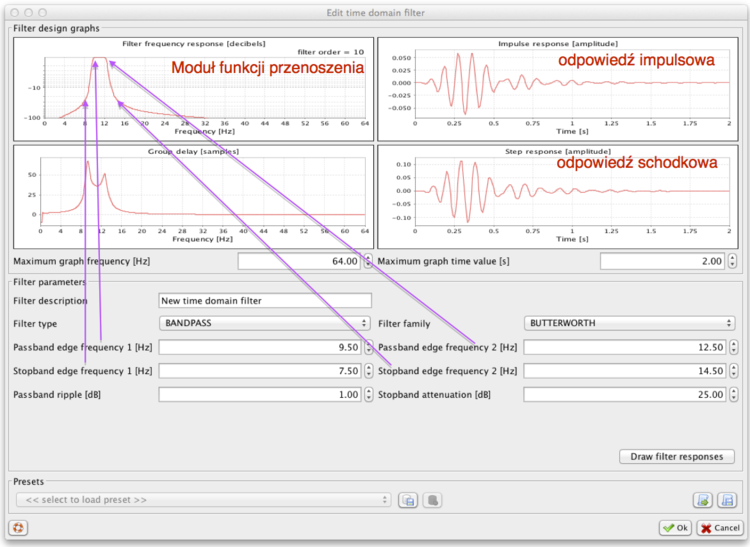
Projektowanie filtrów w programie Svarog
Program SVAROG ma wygodne narzędzie do projektowania filtrów IIR. Zanim przejdziemy do implementowania tych filtrów w pythonie, spróbujemy nabrać wyczucia w SVAROGU.
W celu zaprojektowania filtru w Svarogu należy sprecyzować następujące parametry:
- Typ filtru - dolnoprzepustowy, górnoprzepustowy, pasmowoprzepustowy, pasmowozaporowy.
- Rodzaj filtru - Butterwortha, Czebyszewa I i II, eliptyczny.
- Częstotliwość graniczna pasma przepustowego 1 - górna częstotliwość pasma przenoszenia oddzielająca pasmo przenoszenia od obszaru przejściowego.
- Częstotliwość graniczna pasma przepustowego 2 - w przypadku filtru pasmowoprzepustowego lub pasmowozaporowego istnieją dwa obszary przejściowego; w związku z tym częstotliwość graniczna 1 oddziela pasmo przenoszenia od pierwszego obszaru przejściowego (ma niższą wartość), a częstotliwość graniczna 2 separuje pasmo przenoszenia od drugiego obszaru przejściowego.
- Częstotliwość graniczna pasma zaporowego 1 - dolna częstotliwość pasma zaporowego oddzielająca pasmo zaporowe od obszaru przejściowego.
- Częstotliwość graniczna pasma zaporowego 2 - w przypadku filtru pasmowoprzepustowego lub pasmowozaporowego częstotliwość graniczna 1 oddziela pasmo zaporowe od pierwszego obszaru przejściowego (ma niższą wartość), a częstotliwość graniczna 2 separuje pasmo zaporowe od drugiego obszaru przejściowego.
- Zafalowania w paśmie przenoszenia - maksymalna wartość tłumienia w paśmie przenoszenia.
- Tłumienie w paśmie zaporowym - minimalna wartość tłumienia w paśmie zaporowym.
Przykład
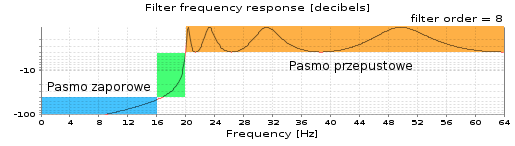
Rysunek poniżej przedstawia charakterystykę amplitudową górnoprzepustowego filtru Czebyszewa I. Filtr został zaprojektowany przy użyciu następujących parametrów:
- Filter type = high-pass
- Filter family = Chebyshev I
- Passband edge frequency 1 = 20 Hz
- Stopband edge frequency 1 = 16 Hz
- Passband ripple = 3 dB
- Stopband attenuation = 40 dB
Rząd filtru zostaje dostosowany do wymagań projektowych.
Zadanie
Przydadzą nam się pliki: Plik z sygnałem EKG Plik z metadanymi do tego sygnału
Analiza_sygnałów_-_ćwiczenia/Filtry