WnioskowanieStatystyczne/ROC: Różnice pomiędzy wersjami
| Linia 5: | Linia 5: | ||
Pojęcia błędów I i II rodzaju, podobnie jak hipotezy zerowej (H<sub>0</sub>) wprowadzili do statystyki [https://pl.wikipedia.org/wiki/Jerzy_Spława-Neyman Jerzy Spława-Neyman] i [https://pl.wikipedia.org/wiki/Egon_Pearson Egon Pearson] w latach 30. XX wieku. | Pojęcia błędów I i II rodzaju, podobnie jak hipotezy zerowej (H<sub>0</sub>) wprowadzili do statystyki [https://pl.wikipedia.org/wiki/Jerzy_Spława-Neyman Jerzy Spława-Neyman] i [https://pl.wikipedia.org/wiki/Egon_Pearson Egon Pearson] w latach 30. XX wieku. | ||
| − | Przyjęcie poziomu istotności (<math>\alpha</math>) na poziomie 5 procent oznacza, że średnio w jednym na dwadzieścia przypadków możemy odrzucić prawdziwą hipotezę, czyli popełnić [https://pl.wikipedia.org/wiki/Błąd_pierwszego_rodzaju '''błąd I rodzaju'''] (false positive, FP). | + | Przyjęcie poziomu istotności (<math>\alpha</math>) na poziomie 5 procent oznacza, że średnio w jednym na dwadzieścia przypadków możemy odrzucić prawdziwą hipotezę, czyli popełnić [https://pl.wikipedia.org/wiki/Błąd_pierwszego_rodzaju '''błąd I rodzaju'''] (false positive, ''FP''). |
| − | [https://pl.wikipedia.org/wiki/Błąd_drugiego_rodzaju '''Błąd II rodzaju'''] polega na przyjęciu hipotezy fałszywej (false negative, FN). | + | [https://pl.wikipedia.org/wiki/Błąd_drugiego_rodzaju '''Błąd II rodzaju'''] polega na przyjęciu hipotezy fałszywej (false negative, ''FN''). |
Wersja z 14:08, 27 kwi 2023
Wnioskowanie_Statystyczne_-_wykład
Błędy I i II rodzaju
Pojęcia błędów I i II rodzaju, podobnie jak hipotezy zerowej (H0) wprowadzili do statystyki Jerzy Spława-Neyman i Egon Pearson w latach 30. XX wieku.
Przyjęcie poziomu istotności ([math]\alpha[/math]) na poziomie 5 procent oznacza, że średnio w jednym na dwadzieścia przypadków możemy odrzucić prawdziwą hipotezę, czyli popełnić błąd I rodzaju (false positive, FP).
Błąd II rodzaju polega na przyjęciu hipotezy fałszywej (false negative, FN).
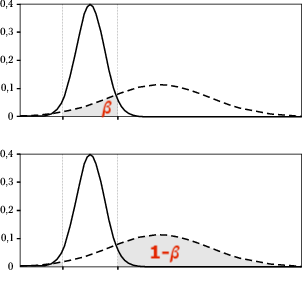
[math]\textrm{P}(FP) = \alpha, \textrm{P}(FN) = \beta[/math], moc testu = [math]1-\beta[/math].
| hipoteza H0 | |||
| Prawdziwa | Fałszywa | ||
|---|---|---|---|
| decyzja | Odrzuć | błąd typu I (False Positive, [math]p=\alpha[/math]) | poprawna (True Positive), [math]p=1-\beta[/math] |
| Przyjmij | poprawna (True Negative, [math]p=1-\alpha[/math]) | błąd typu II (False Negative), [math]p=\beta[/math] | |
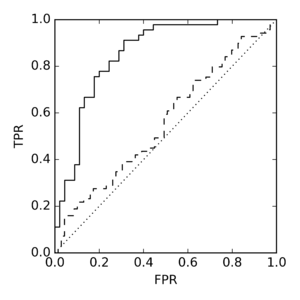
Krzywa ROC (receiver operating characteristic)
[math]TPR = \dfrac{TP}{P} = \dfrac{TP}{TP+FN}[/math] — czułość (sensitivity), true positive rate
[math]TNR = \dfrac{TN}{N} = \dfrac{TN}{FP + TN}[/math] — swoistość (specificity), true negative rate
[math]FPR = \dfrac{FP}{N} = \dfrac{FP}{FP + TN} = \dfrac{FP + TN - TN}{FP + TN} = 1 - TNR[/math]
Opisane powyżej błędy odnoszą się do ostatecznych, binarnych decyzji systemu (np. przynależność do grupy A lub B). Jednak bardzo często system na "przedostatnim" stadium zwraca wielkość odpowiadającą prawdopodobieństwu przynależności do jednej z grup. Dopiero wybranie progu daje nam decyzję binarną. Ten próg możemy dobierać w zależności od tego, czy ważniejsze jest unikanie FP czy maksymalizowanie TP.
Kwestie doboru progu ładnie ilustruje obrazek z Wikipedii.
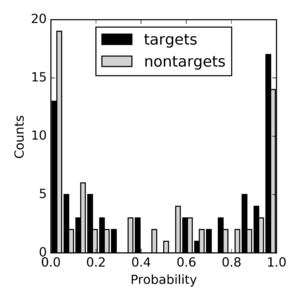
Na poniższych ilustracjach Rys. 2 i Rys. 3 z artykułu dostępnego w Internecie przedstawiono histogramy decyzji klasyfikatora, który przypisywał odcinkom EEG prawdopodobieństwo faktu, że wystąpił w nim potencjał wywołany, który związany jest z koncentracją uwagi na bodźcu wyświetlanym w danym momencie. Jako "ground truth", czyli kryterium, przyjęto deklarowane przez użytkowników intencje zwracania uwagi na dany bodziec (target) lub nie (nontarget).
AUC (inaczej AUROC, czyli Area Under ROC) to pole pod krzywą ROC, określające jakość separacji rozkładów dla różnych ustawień progu.