WnioskowanieStatystyczne/Elementy statystyki wielowymiarowej: Różnice pomiędzy wersjami

Z Brain-wiki
 
(Nie pokazano 69 pośrednich wersji utworzonych przez tego samego użytkownika)
Linia 38: Linia 38:
 
niezależnych korelacja wynosi <math>0</math>.
 
niezależnych korelacja wynosi <math>0</math>.
  
−
==Macierz kowariancji==
+
 
 +
 
 +
===Macierz kowariancji===
  
  
Linia 47: Linia 49:
  
  
−
dla <math>x=(x_{1,}x_{2})</math> i <math>\mu =(\mu _{1}, \mu _{2})</math>  
+
dla dwóch wymiarów: <math>x=(x_{1,}x_{2})</math> i <math>\mu =(\mu _{1}, \mu _{2})</math>  
  
  
Linia 76: Linia 78:
 
\end{matrix}
 
\end{matrix}
 
\right]
 
\right]
 +
</math>
 +
 +
 +
ogólnie
 +
 +
 +
<math>
 +
S=\left[
 +
\begin{matrix}
 +
\upsilon ar(x_{1}) & co\upsilon (x_{1},x_{2}) & ... & co\upsilon
 +
(x_{1},x_{k}) \\
 +
co\upsilon (x_{2},x_{1}) & \upsilon ar(x_{2}) & ... & co\upsilon
 +
(x_{2},x_{k}) \\
 +
... & ... & ... & ... \\
 +
co\upsilon \left( x_{k},x_{1}\right) & co\upsilon (x_{k},x_{2}) & ... &
 +
\upsilon ar(x_{k})
 
\end{matrix}
 
\end{matrix}
 +
\right]
 
</math>
 
</math>
  
  
  
−
Interpretacja współczynnika korelacji znajduje się pod hasłem ''Regresja liniowa''.
 
  
−
==Dwumianowy rozkład normalny==
+
<!--
 +
==Dwuwymiarowy rozkład normalny==
 +
 
 
<math>
 
<math>
 
f(t)=ke^{-\frac{1}{2}(t-\mu )A(t-\mu )^{T}}
 
f(t)=ke^{-\frac{1}{2}(t-\mu )A(t-\mu )^{T}}
Linia 94: Linia 114:
 
<math>\mu =(\mu _{1},\mu _{2})-</math> wektor wartości oczekiwanych
 
<math>\mu =(\mu _{1},\mu _{2})-</math> wektor wartości oczekiwanych
  
−
<math>k-</math> stała normalizjąca
+
<math>k-</math> stała normalizująca
  
 
<math>A-</math> odwrotność macierzy kowariancji <math>C</math>  
 
<math>A-</math> odwrotność macierzy kowariancji <math>C</math>  
Linia 113: Linia 133:
 
</math>
 
</math>
  
 +
-->
  
 +
==Analiza wariancji wielu zmiennych (''Multivariate ANalysis of VAriance &mdash; MANOVA'')==
  
−
==Analiza wariancji wielu zmiennych (''Multivariate ANalysis of VAriance &mdash; MANOVA'')==
+
Wcześniej rozpatrywaliśmy podział na grupy pomiarów opisanych jedną zmienną ([[WnioskowanieStatystyczne/Analiza_wariancji|analiza wariancji jednej zmiennej]]). Jeśli zmienna losowa <math>X</math> jest opisana wektorem
 +
(<math>x_{1},...,x_{k})</math>, wartość
 +
wektorem o tym samym wymiarze: (<math> \mu _{1},...,\mu _{k})</math>, to
 +
w miejsce wariancji mamy do czynienia z macierzą kowariancji:
  
−
Zmienna losowa <math>X</math> opisywana wektorem
 
−
(<math>x_{1},...,x_{k})</math>, podobnie wartość średnia staje się
 
−
wektorem o tym samym wymiarze: (<math> \mu _{1},...,\mu _{k}).</math>
 
−
Macierz kowariancji zmiennej losowej
 
  
 
<math>
 
<math>
Linia 135: Linia 156:
 
\right]
 
\right]
 
</math>
 
</math>
 +
  
 
gdzie:  
 
gdzie:  
 +
  
 
<math>
 
<math>
 
\upsilon ar(x_{i})=\sigma _{x_{i}}=E((x_{i}-\mu _{i})^{2})
 
\upsilon ar(x_{i})=\sigma _{x_{i}}=E((x_{i}-\mu _{i})^{2})
 
</math>
 
</math>
 +
  
 
<math>
 
<math>
Linia 146: Linia 170:
 
_{k}))
 
_{k}))
 
</math>
 
</math>
 +
 +
  
 
Zakladamy, że dane pochodzą z wielowymiarowego rozkładu normalnego, opisanego macierzą kowariancji <math>S</math>
 
Zakladamy, że dane pochodzą z wielowymiarowego rozkładu normalnego, opisanego macierzą kowariancji <math>S</math>
 +
  
 
<math>
 
<math>
Linia 153: Linia 180:
 
)^{\prime }S^{-1}(X-\mu )}{2}}
 
)^{\prime }S^{-1}(X-\mu )}{2}}
 
</math>
 
</math>
 +
  
 
Jeśli <math>X</math> pochodzą z próby
 
Jeśli <math>X</math> pochodzą z próby
Linia 164: Linia 192:
 
</math>
 
</math>
  
−
Jako statystykę testową możemy wtbrać np. iloraz wyznaczników
+
Jako statystykę testową możemy wybrać np. iloraz wyznaczników
 
macierzy <math>S_{wew}</math> i <math>S</math>, który podlega rozkładowi
 
macierzy <math>S_{wew}</math> i <math>S</math>, który podlega rozkładowi
 
<math>\Lambda </math> Wilksa:
 
<math>\Lambda </math> Wilksa:
 +
  
 
<math>
 
<math>
Linia 172: Linia 201:
 
</math>
 
</math>
  
 +
=Uczenie (maszynowe, ML) nienadzorowane (unsupervised learning)=
  
  
  
 
==Analiza składowych głównych (''Principal Components Analysis, PCA'')==
 
==Analiza składowych głównych (''Principal Components Analysis, PCA'')==
 +
Jeśli zmienne są bardzo silnie skorelowane, mamy do czynienia z redundancją. Możemy ją zmniejszyć,  redukując wymiar danych. W tym celu macierz kowariancji
 +
 +
 +
<math>
 +
S=\left[
 +
\begin{matrix}
 +
\upsilon ar(x_{1}) & co\upsilon (x_{1},x_{2}) & ... & co\upsilon
 +
(x_{1},x_{k}) \\
 +
co\upsilon (x_{2},x_{1}) & \upsilon ar(x_{2}) & ... & co\upsilon
 +
(x_{2},x_{k}) \\
 +
... & ... & ... & ... \\
 +
co\upsilon \left( x_{k},x_{1}\right) & co\upsilon (x_{k},x_{2}) & ... &
 +
\upsilon ar(x_{k})
 +
\end{matrix}
 +
\right]
 +
</math>
 +
 +
 +
przedstawiamy w postaci diagonalnej
  
−
Przedstawiamy macierz kowariancji w postaci diagonalnej
 
  
 
<math>
 
<math>
Linia 203: Linia 251:
 
\right]
 
\right]
 
</math>
 
</math>
 +
  
 
Wielkości <math>\lambda _{i}</math> są rozwiązaniami równania
 
Wielkości <math>\lambda _{i}</math> są rozwiązaniami równania
 
<math>\left| S-\lambda I\right| =0,</math> a wektor <math>r_{i}</math>
 
<math>\left| S-\lambda I\right| =0,</math> a wektor <math>r_{i}</math>
−
osiami nowego układu współrzędnych. Składowe <math>PCA</math> są
+
osiami nowego układu współrzędnych. Składowe PCA są
 
liniowymi kombinacjami obserwowanych zmiennych.
 
liniowymi kombinacjami obserwowanych zmiennych.
  
−
[[Plik:pca.png|right|thumb|600px|Kierunki składowych głównych (PCA) w dwóch wymiarach]]
 
  
−
==Analiza dyskryminacyjna (''Discriminant Analysis'' )==
 
  
−
Wielowymiarowe wektory próby <math>X</math> mamy podzielone na grupy,
+
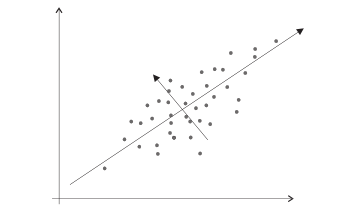
[[Plik:pca.png|center|thumb|600px|Kierunki składowych głównych (PCA) w dwóch wymiarach]]
−
szukamy funkcji najlepiej je rozdzielającej, która umożliwi
 
−
zaklasyfikowanie nowej obserwacji. Rozdzielenie grup odpowiada w
 
−
przypadku jednowymiarowym maksymalizacji stosunku wariancji
 
−
międzygrupowej do wariancji wewnątrzgrupowej
 
  
−
<math>
+
==Analiza skupień &mdash; ''Cluster Analysis'' ==
−
F=\frac{\left( n-k\right) s_{pom}}{\left( k-1\right) s_{wew}}
 
−
</math>
 
−
 
 
−
W przypadku wielowymiarowym mamy do czynienia z macierzami kowariancji;
 
−
możemy rozpatrywać wielkość
 
−
 
 
−
<math>
 
−
F_{a}=\frac{a^{\prime }S_{pom}a}{a^{\prime }S_{wew}a}
 
−
</math>
 
−
 
 
−
Maksymalizacja tej wielkości względem <math>a</math> daje wektor
 
−
własny macierzy <math>S_{wew}^{-1}S_{pom}</math> odpowiadający
 
−
największej wartości własnej. Wektory własne odpowiadające kolejnym
 
−
wartościom własnym zwiemy współrzędnymi dyskryminacyjnymi, tworzącymi
 
−
przestrzeń dyskryminacyjną.
 
  
−
==Analiza czynnikowa (''Factor Analysis'' )==
+
Wejściem dla tej klasy procedury są nieoznaczone dane, a wyjściem ich podział
 +
na grupy. Obecnie metody tego typu określamy czasem jako "unsupervised learning".
  
−
opiera się na założeniu istnienia ukrytych czynników, stara się
+
<!-- Można go zrealizować na wiele sposobów: <math>N</math>
−
przedstawić obserwowane zmienne w postaci:
 
−
<blockquote>
 
−
obserwowana zmienna = liniowa kombinacja czynników + błąd
 
−
</blockquote>
 
−
w odróżnieniu od PCA, realizującej model
 
−
<blockquote>
 
−
składowa = liniowa kombinacja obserwowanych zmiennych
 
−
</blockquote>
 
−
 
 
−
==Analiza skupień &mdash; ''Cluster Analysis'' ==
 
−
 
 
−
Wejściem dla tej procedury jest zestaw danych, a wyjściem ich podział
 
−
na grupy. Można go zrealizować na wiele sposobów: <math>N</math>
 
 
punktów <math>x^{1}...x^{N},</math> z których każdy opisany jest przez
 
punktów <math>x^{1}...x^{N},</math> z których każdy opisany jest przez
−
<math>k</math> cech <math>x_{1}...x_{k}</math>.
+
<math>k</math> cech <math>x_{1}...x_{k}</math>. -->
  
 
===Metody polegające na kolejnym łączeniu punktów===
 
===Metody polegające na kolejnym łączeniu punktów===
Linia 270: Linia 286:
 
Odległości między klastrami:
 
Odległości między klastrami:
 
    
 
    
−
* Najbliższego sąsiada ''(single linkage)''  - odległość  między dwoma najbliższymi elementami klastrów <math>A</math> i <math>B</math>:  <math>d(A,B)=\min_{x,y}d(x,y),\ \ \ \ \ x\in A,\ y\in B</math>     
+
* Najbliższego sąsiada ''(single linkage)''  - odległość  między dwoma najbliższymi elementami klastrów ''A'' i ''B'':  <math>d(A,B)=\min_{x,y}d(x,y),\ \ \ \ \ x\in A,\ y\in B</math>     
−
*(''complete linkage'' ) - odległość między dwoma  najbliższymi elementami klastrów <math>A</math> i <math>B</math>:  <math>d(A,B)=\max_{x,y}d(x,y),\ \ \ \ \ x\in A,\ y\in B  </math>   
+
*(''complete linkage'' ) - odległość między dwoma  najbliższymi elementami klastrów ''A'' i ''B'':  <math>d(A,B)=\max_{x,y}d(x,y),\ \ \ \ \ x\in A,\ y\in B  </math>   
 
*''(centroid)''  - odległość między środkami  klastrów,     
 
*''(centroid)''  - odległość między środkami  klastrów,     
−
*''(avarage)''  - średnia odległości, itd...
+
*''(average)''  - średnia odległości, itd...
 +
 
  
 
===Metoda K&ndash;średnich (''K &ndash; means'' )===
 
===Metoda K&ndash;średnich (''K &ndash; means'' )===
Linia 279: Linia 296:
 
Wybieramy ilość klastrów, podział dokonywany jest w iteracyjnej
 
Wybieramy ilość klastrów, podział dokonywany jest w iteracyjnej
 
procedurze dążącej do minimalizacji stosunku wariancji pomiędzy
 
procedurze dążącej do minimalizacji stosunku wariancji pomiędzy
−
klastrami do wariancji wewnątrz klastrów - niejako <math>ANOVA</math>
+
klastrami do wariancji wewnątrz klastrów — niejako <math>ANOVA</math>
 
bez ustalonego wstępnie przyporządkowania, maksimum <math> F</math>
 
bez ustalonego wstępnie przyporządkowania, maksimum <math> F</math>
 
poszukiwane drogą przemieszczania elementów między klastrami.
 
poszukiwane drogą przemieszczania elementów między klastrami.

Aktualna wersja na dzień 18:25, 1 cze 2023

Wnioskowanie_Statystyczne_-_wykład


Elementy statystyki wielowymiarowej

Przypomnijmy najpierw pojęcia

Kowariancja i współczynnik korelacji

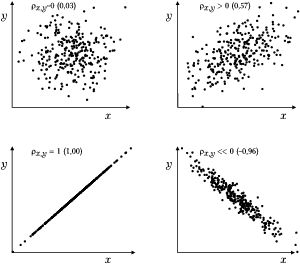
Przykładowe wartości współczynnika korelacji dla 300 par [math](x, y)[/math] o różnych stopniach współzależności.

Miarą związku między zmiennymi [math]x[/math] i [math]y[/math] jest kowariancja

[math] \sigma_{x, y} = E\left( (x-\mu_{x})(y-\mu_{y})\right) [/math]

lub unormowany do jedności współczynnik korelacji zmiennych [math]x[/math] i [math]y[/math]:

[math] \rho_{x, y}= \frac{\sigma_{x, y}}{\sigma_x \sigma_y}= \frac{E\left( \left(x-\mu_{x})(y-\mu_{y}\right)\right)} {\sqrt{E\left( (x-\mu_{x})^2\right) E\left( (y-\mu_{y})^2\right)}}, [/math]

gdzie [math]\mu_x[/math] i [math]\mu_y[/math] to odpowiednio wartości oczekiwane zmiennych [math]x[/math] i [math]y[/math]. Jeśli zmienne [math]x[/math] i [math]y[/math] związane są deterministyczną zależnością liniową (typu [math]y=c_1 x+c_2[/math]), to ich korelacja wynosi [math]1[/math] (lub [math]-1[/math], jeśli [math]c_1\lt 0[/math]). Jeśli wzrostowi zmiennej [math]x[/math] towarzyszy statystycznie wzrost zmiennej [math]y[/math], to ich korelacja jest dodatnia (pomiędzy [math]0[/math] a [math]1[/math]). Dla zmiennych niezależnych korelacja wynosi [math]0[/math].


Macierz kowariancji

[math] C=E[(x-\mu )(x-\mu )^{T}], \qquad \\ c_{ij}=E[(x_{i}-\mu_{i})(x_{j}-\mu _{j})] [/math]


dla dwóch wymiarów: [math]x=(x_{1,}x_{2})[/math] i [math]\mu =(\mu _{1}, \mu _{2})[/math]


[math] C=E\left[ \left(\begin{matrix}{x_{1}-\mu _{1}}\\ {x_{2}-\mu _{2}} \end{matrix} \right) \left( x_{1}-\mu_{1},x_{2}-\mu _{2}\right) \right] = [/math]

[math] \left[ \begin{matrix} E\left[ \left( x_{1}-\mu _{1}\right) ^{2}\right] & E\left[ \left( x_{1}-\mu _{1}\right) \left( x_{2}-\mu _{2}\right) \right] \\ E\left[ \left( x_{2}-\mu _{2}\right) \left( x_{1}-\mu _{1}\right) \right] & E \left[ \left( x_{2}-\mu _{2}\right) ^{2}\right] \end{matrix} \right] = [/math]


[math] \left[ \begin{matrix} \sigma _{1}^{2} & \sigma _{12} \\ \sigma _{21} & \sigma _{2}^{2} \end{matrix} \right] [/math]


ogólnie


[math] S=\left[ \begin{matrix} \upsilon ar(x_{1}) & co\upsilon (x_{1},x_{2}) & ... & co\upsilon (x_{1},x_{k}) \\ co\upsilon (x_{2},x_{1}) & \upsilon ar(x_{2}) & ... & co\upsilon (x_{2},x_{k}) \\ ... & ... & ... & ... \\ co\upsilon \left( x_{k},x_{1}\right) & co\upsilon (x_{k},x_{2}) & ... & \upsilon ar(x_{k}) \end{matrix} \right] [/math]



Analiza wariancji wielu zmiennych (Multivariate ANalysis of VAriance — MANOVA)

Wcześniej rozpatrywaliśmy podział na grupy pomiarów opisanych jedną zmienną (analiza wariancji jednej zmiennej). Jeśli zmienna losowa [math]X[/math] jest opisana wektorem ([math]x_{1},...,x_{k})[/math], wartość wektorem o tym samym wymiarze: ([math] \mu _{1},...,\mu _{k})[/math], to w miejsce wariancji mamy do czynienia z macierzą kowariancji:


[math] S=\left[ \begin{matrix} \upsilon ar(x_{1}) & co\upsilon (x_{1},x_{2}) & ... & co\upsilon (x_{1},x_{k}) \\ co\upsilon (x_{2},x_{1}) & \upsilon ar(x_{2}) & ... & co\upsilon (x_{2},x_{k}) \\ ... & ... & ... & ... \\ co\upsilon \left( x_{k},x_{1}\right) & co\upsilon (x_{k},x_{2}) & ... & \upsilon ar(x_{k}) \end{matrix} \right] [/math]


gdzie:


[math] \upsilon ar(x_{i})=\sigma _{x_{i}}=E((x_{i}-\mu _{i})^{2}) [/math]


[math] co\upsilon (x_{i},x_{k})=\sigma _{x_{i},x_{k}}=E((x_{i}-\mu _{i})(x_{k}-\mu _{k})) [/math]


Zakladamy, że dane pochodzą z wielowymiarowego rozkładu normalnego, opisanego macierzą kowariancji [math]S[/math]


[math] \Phi (X)=\frac{1}{\sqrt{(2\pi )^{k}}\sqrt{\left| S\right| }}e^{-\frac{(X-\mu )^{\prime }S^{-1}(X-\mu )}{2}} [/math]


Jeśli [math]X[/math] pochodzą z próby podzielonej na grupy, to podobnie jak w ANOVA możemy skonstruować macierze wariancji wewnątrzgrupowych i międzygrupowych i dowieść, że [math]S=S_{wew}+S_{pom}[/math].

Testujemy hipotezę o równości średnich w grupach

[math] H_0: \mu_1 = \mu_2 = \cdots = \mu_k [/math]

Jako statystykę testową możemy wybrać np. iloraz wyznaczników macierzy [math]S_{wew}[/math] i [math]S[/math], który podlega rozkładowi [math]\Lambda [/math] Wilksa:


[math] \Lambda =\frac{\left| S_{wew}\right| }{\left| S\right| }=\frac{\left| S_{wew}\right| }{\left| S_{wew}+S_{pom}\right| } [/math]

Uczenie (maszynowe, ML) nienadzorowane (unsupervised learning)

Analiza składowych głównych (Principal Components Analysis, PCA)

Jeśli zmienne są bardzo silnie skorelowane, mamy do czynienia z redundancją. Możemy ją zmniejszyć, redukując wymiar danych. W tym celu macierz kowariancji


[math] S=\left[ \begin{matrix} \upsilon ar(x_{1}) & co\upsilon (x_{1},x_{2}) & ... & co\upsilon (x_{1},x_{k}) \\ co\upsilon (x_{2},x_{1}) & \upsilon ar(x_{2}) & ... & co\upsilon (x_{2},x_{k}) \\ ... & ... & ... & ... \\ co\upsilon \left( x_{k},x_{1}\right) & co\upsilon (x_{k},x_{2}) & ... & \upsilon ar(x_{k}) \end{matrix} \right] [/math]


przedstawiamy w postaci diagonalnej


[math] S=\left[ \begin{matrix} r_{11} & r_{12} & ... & r_{1k} \\ r_{21} & r_{22} & ... & r_{2k} \\ ... & ... & ... & ... \\ r_{k1} & r_{k2} & ... & r_{kk} \end{matrix} \right] \left[ \begin{matrix} \lambda _{1} & 0 & ... & 0 \\ 0 & \lambda _{2} & ... & 0 \\ ... & ... & ... & ... \\ 0 & 0 & ... & \lambda _{k} \end{matrix} \right] \left[ \begin{matrix} r_{11} & r_{21} & ... & r_{k1} \\ r_{12} & r_{22} & ... & r_{k2} \\ ... & ... & ... & ... \\ r_{1k} & r_{2k} & ... & r_{kk} \end{matrix} \right] [/math]


Wielkości [math]\lambda _{i}[/math] są rozwiązaniami równania [math]\left| S-\lambda I\right| =0,[/math] a wektor [math]r_{i}[/math] osiami nowego układu współrzędnych. Składowe PCA są liniowymi kombinacjami obserwowanych zmiennych.


Kierunki składowych głównych (PCA) w dwóch wymiarach

Analiza skupień — Cluster Analysis

Wejściem dla tej klasy procedury są nieoznaczone dane, a wyjściem ich podział na grupy. Obecnie metody tego typu określamy czasem jako "unsupervised learning".


Metody polegające na kolejnym łączeniu punktów

Startujemy z N klastrów jednopunktowych, w każdym kroku łączymy najbliższe. Wynikiem działania jest drzewo łączenia, na którym sami musimy wybrać ilość klastrów. Wynik zależy silnie od przyjętych definicji odległości między klastrami oraz definicji odległości między punktami.

Odległości między punktami:

  • Odległość Euklidesowa [math]d(x,y)=\sqrt{\underset{i=1}{\overset{k}{\sum }}(x_{i}-y_{i})^{2}}[/math] (czuła na różne skale cech).
  • Odległość korelacyjna [math]d(x,y)=1-\rho (x,y),[/math] gdzie [math]\rho (x,y)=\frac{\underset{i=1}{\overset{k}{\sum }}(x-\overline{x})(y- \overline{y})}{\sigma _{x}\sigma _{y}} [/math] (znormalizowana do przedziału (0,2), mniejsza im lepiej skorelowane punkty).

Odległości między klastrami:

  • Najbliższego sąsiada (single linkage) - odległość między dwoma najbliższymi elementami klastrów A i B: [math]d(A,B)=\min_{x,y}d(x,y),\ \ \ \ \ x\in A,\ y\in B[/math]
  • (complete linkage ) - odległość między dwoma najbliższymi elementami klastrów A i B: [math]d(A,B)=\max_{x,y}d(x,y),\ \ \ \ \ x\in A,\ y\in B [/math]
  • (centroid) - odległość między środkami klastrów,
  • (average) - średnia odległości, itd...


Metoda K–średnich (K – means )

Wybieramy ilość klastrów, podział dokonywany jest w iteracyjnej procedurze dążącej do minimalizacji stosunku wariancji pomiędzy klastrami do wariancji wewnątrz klastrów — niejako [math]ANOVA[/math] bez ustalonego wstępnie przyporządkowania, maksimum [math] F[/math] poszukiwane drogą przemieszczania elementów między klastrami.

Źródło: „http://brain.fuw.edu.pl/edu/index.php?title=WnioskowanieStatystyczne/Elementy_statystyki_wielowymiarowej&oldid=9450”