Spektrogram: Różnice pomiędzy wersjami
| (Nie pokazano 2 pośrednich wersji utworzonych przez tego samego użytkownika) | |||
| Linia 1: | Linia 1: | ||
| + | |||
| + | <!-- | ||
| + | [[Plik:Svarog wav.png|800px|bezramki]] | ||
| + | --> | ||
==[[Analiza_sygnałów_-_lecture|AS/]] Spektrogram — oknowana transformata Fouriera== | ==[[Analiza_sygnałów_-_lecture|AS/]] Spektrogram — oknowana transformata Fouriera== | ||
| Linia 12: | Linia 16: | ||
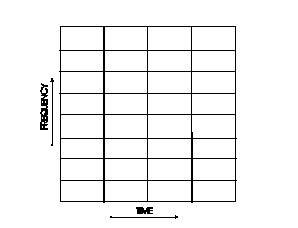
[[Plik:timefreq_rys_3.jpg|thumb|center|400px|<figure id="fig:6"></figure>Równomierny podział przestrzeni czas-częstość dla oknowanej transformaty Fouriera]] | [[Plik:timefreq_rys_3.jpg|thumb|center|400px|<figure id="fig:6"></figure>Równomierny podział przestrzeni czas-częstość dla oknowanej transformaty Fouriera]] | ||
| + | |||
| + | |||
| + | ==[[Analiza_sygnałów_-_lecture|AS/]] Falki ''(wavelets)''== | ||
| + | Falka to funkcja <math>\psi \in L^2(\mathbb{R})</math> o zerowej średniej: | ||
| + | <center><math> | ||
| + | \int_{-\infty}^{\infty}\psi(t) dt = 0 | ||
| + | </math></center> | ||
| + | |||
| + | Aby spełnić ten warunek, niezerowa funkcja musi oscylować, choć | ||
| + | niekoniecznie (wręcz raczej nie) w sposób okresowy, jak "duże" fale | ||
| + | <math>e^{ikt}</math>—stąd nazwa. | ||
| + | |||
| + | Reprezentacja konstruowana jest ze "współczynników falkowych" — | ||
| + | iloczynów skalarnych sygnału ze znormalizowanymi | ||
| + | (<math>\|\psi\|=1</math>) funkcjami generowanymi jako przesunięcia i | ||
| + | rozciągnięcia falki <math>\psi</math>: | ||
| + | <center><math> c_{s,u} = \langle s \psi_{s,u}\rangle = \int_{-\infty}^{\infty} s(t) | ||
| + | \psi (\frac{t-u}{s}) dt </math></center> | ||
| + | |||
| + | Transformacja odwrotna istnieje, jeśli zbiór falek | ||
| + | <math>\left\{\psi_i\right\}_{i\in I}</math> tworzy ramę | ||
| + | (ang. ''frame'' ): | ||
| + | <center><math> | ||
| + | \forall_f \exists_{A>0, B<\infty} A\|s\|^2 \le \sum_{i\in I} |\langle\psi_i, s\rangle|^2 \le B\|s\|^2 | ||
| + | </math></center> | ||
| + | |||
| + | Dopiero w latach 80. XX wieku udowodniono, że ze specjalnie dobranych | ||
| + | falek można skonstruować ortogonalną bazę, jeśli kolejne skale | ||
| + | <math>s</math> będą tworzyły sekwencję diadyczną, czyli | ||
| + | <math>s_n=2^ns_0</math>. Doprowadziło to do eksplozji zastosowań | ||
| + | czasowo-częstościowych metod analizy sygnałów — nie tylko ze względu | ||
| + | na cenione przez fizyków własności baz ortogonalnych, jak zachowanie | ||
| + | energii reprezentacji czy prosta formuła rekonstrukcji, ale głównie | ||
| + | dzięki powstaniu szybkich algorytmów obliczeniowych. | ||
| + | |||
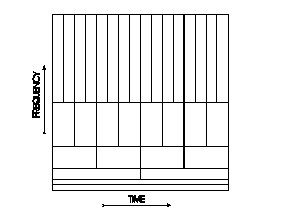
| + | [[Plik:timefreq_rys_4.jpg|thumb|center|400px|Podział przestrzeni czas-częstość dla wielorozdzielczej analizy falkowej.]] | ||
Aktualna wersja na dzień 08:45, 14 gru 2025
AS/ Spektrogram — oknowana transformata Fouriera
Przepis na krótkoczasową transformatę Fouriera (Short-Time Fourier Transform, STFT ) polega na wycinaniu kolejnych odcinków sygnału z pomocą okna [math]g(t)[/math] ([math]\|g\|=1[/math]) i obliczaniu ich transformaty Fouriera. Inaczej można to opisać jako iloczyny skalarne sygnału z oknem [math]g[/math] modulowanym częstością [math]\xi[/math]:
Moduł współczynnika [math]c_{\xi, t_0}[/math] mówi o zawartości energii sygnału [math]s(t)[/math] w okolicy częstości [math]\xi[/math] i czasu [math]t_0[/math]
AS/ Falki (wavelets)
Falka to funkcja [math]\psi \in L^2(\mathbb{R})[/math] o zerowej średniej:
Aby spełnić ten warunek, niezerowa funkcja musi oscylować, choć niekoniecznie (wręcz raczej nie) w sposób okresowy, jak "duże" fale [math]e^{ikt}[/math]—stąd nazwa.
Reprezentacja konstruowana jest ze "współczynników falkowych" — iloczynów skalarnych sygnału ze znormalizowanymi ([math]\|\psi\|=1[/math]) funkcjami generowanymi jako przesunięcia i rozciągnięcia falki [math]\psi[/math]:
Transformacja odwrotna istnieje, jeśli zbiór falek [math]\left\{\psi_i\right\}_{i\in I}[/math] tworzy ramę (ang. frame ):
Dopiero w latach 80. XX wieku udowodniono, że ze specjalnie dobranych falek można skonstruować ortogonalną bazę, jeśli kolejne skale [math]s[/math] będą tworzyły sekwencję diadyczną, czyli [math]s_n=2^ns_0[/math]. Doprowadziło to do eksplozji zastosowań czasowo-częstościowych metod analizy sygnałów — nie tylko ze względu na cenione przez fizyków własności baz ortogonalnych, jak zachowanie energii reprezentacji czy prosta formuła rekonstrukcji, ale głównie dzięki powstaniu szybkich algorytmów obliczeniowych.