Funkcja wykładnicza i logarytmiczna: Różnice pomiędzy wersjami

Z Brain-wiki
(Utworzono nową stronę "__NOTOC__ ==Zasada indukcji matematycznej== Zbiór liczb naturalnych posiada bardzo ważną własność, której często się używa w dowodach. Mówi ona że: Niech...")
 
 
Linia 1: Linia 1:
 
__NOTOC__
 
__NOTOC__
  
−
==Zasada indukcji matematycznej==
 
  
−
Zbiór liczb naturalnych posiada bardzo ważną własność, której często się używa w dowodach. Mówi ona że:
+
==Funkcja wykładnicza==
  
−
Niech będzie dana jakaś własność liczb naturalnych (nazwijmy ją '''tezą indukcyjną''') <math>T_n\;</math>,która spełnia następujące warunki:
+
Funkcję wykładniczą definiuje się najsampierw dla wykładników naturalnych.
−
<equation id="eq:1">Liczba 1 posiada tę własność (tzn. teza <math>T_1\;</math> jest prawdziwa),</equation>
+
Dla dowolnego <math>a\in \mathbb R \;</math> oraz <math>n\in \mathbb N \;</math> można zapisać:
−
<equation id="eq:2">Jeśli liczba <math>n\;</math> posiada tę własność, to posiada ją również liczba <math>n+1\;</math> (tzn. prawdziwa jest implikacja: <math>T_n\Longrightarrow T_{n+1}\;</math>)</equation>
+
<equation id="eq:1">
 +
<math>a^n= a\cdot a \dots  a \;\;</math>   (n-razy)
 +
</equation>
 +
Stąd od razu wynika, że:
 +
<equation id="eq:2">
 +
<math>a^n \cdot a^m = a^{n+m}\;\;
 +
</math>
 +
</equation>
 +
oraz
 +
<equation id="eq:3">
 +
<math>
 +
\left(a^n\right)^m=a^{n m}\;\;
 +
</math></equation>
  
−
'''Zasada indukcji''' oznacza, że przy powyższych założeniach, ''każda'' liczba naturalna posiada tę własność (tzn. teza <math>T_n\;</math> jest prawdziwa dla każdej <math>n\in \mathbb N\;</math>). Zasada indukcji odpowiada następującej intuicji: Jeśli prawdziwa jest teza <math>T_1\;</math>, to &mdash; na mocy <xr id="eq:2">(%i)</xr> &mdash; prawdziwa jest również teza <math>T_2\;</math>. Skoro tak, to z <xr id="eq:2">(%i)</xr> prawdziwa jest również teza <math>T_3\;</math>, i znów używając <xr id="eq:2">(%i)</xr> prawdziwa jest teza <math>T_4\;</math> itd.
+
Przyjmujemy, że <math>a^0=1\;</math>.
 +
'''Ujemną potęgę''' definiujemy rozszerzając zasadę <xr id="eq:2">(%i)</xr> przez dopuszczenie, aby <math>n,m\;</math> były  dowolnymi liczbami całkowitymi. Weźmy:
 +
<math>
 +
a^{-n} a^n = a^{-n+n}=a^0=1
 +
\;</math>
 +
skąd
 +
<equation id="eq:4">
 +
<math>
 +
a^{-n}=\frac{1}{a^n}\;\;
 +
</math></equation>
 +
(zakładamy tu, że <math>a\ne 0\;</math>).
  
−
===Przykład &mdash; Nierówność Bernoulliego===
+
Stąd od razu mamy
−
 
+
<equation id="eq:5">
−
Dla każdej liczby naturalnej <math>n\;</math> i każdej liczby rzeczywistej <math>a\geq -1\;</math> zachodzi wzór
+
<math>
−
<equation id="eq:3">
+
\left( \frac{a}{b} \right)^n = \frac{a^n}{b^n}\;
−
<math>(1+a)^n \geq 1+ n a \;
 
 
</math>
 
</math>
 
</equation>
 
</equation>
  
−
#Sprawdzamy prawdziwość tezy <math>T_1\;</math>, tzn. czy nierówność jest prawdziwa dla <math>n=1\;</math>. Mamy: <math>1+a \geq 1+ a\;</math> czyli ok.
+
Definiujemy następnie potęgi '''ułamkowe'''. Tu zakładamy, że <math>a>0\;</math> (zaraz się okaże dlaczego).
−
#Sprawdzamy prawdziwość implikacji <math>T_n\Longrightarrow T_{n+1}\;</math>.
+
 
−
Zapiszmy prawą stronę <math>T_{n+1}\;</math>:
+
Oznaczmy: <math>b=a^\frac{1}{n}\;</math>. Mamy:
−
<center><math>
 
−
(1+a)^{n+1} = (1+a)^n(1+a) \geq (1+na)(1+a) = 1+(n+1)a + na^2 \geq 1+ (n+1)a\;</math></center>
 
−
(korzystamy z założenia o prawdziwości  T_n oraz że <math>(1+a)\geq 0 \;</math>)<br>
 
−
czyli, zakładając prawdziwósć tezy <math>T_n\;</math>, otrzymaliśmy prawdziwość; tezy <math>T_{n+1}\;</math>. Z zasady indukcji wynika więc, że teza <math>T_n\;</math> jest prawdziwa dla każej <math>n\in \mathbb N\;</math> &mdash; tzn. że nierówność <xr id="eq:3">(%i)</xr> jest prawdziwa <math>\forall \, n\in \mathbb N\;</math>
 
  
−
===Przykład &mdash; Dwumian Newtona===
+
<math>
 +
b^n = \left( a^\frac{1}{n}\right)^n = a^{\frac{1}{n}\cdot n} = a^1=a
 +
\;</math>
  
−
Najsampierw jednak zdefiniujemy (a dla tych, co znają, przypomnimy) symbol ''silnia'': <math>n!=1\cdot 2 \cdot 3 \dots (n-1) \cdot n\;</math>, (przyjmujemy też, że <math>0!=1\;</math>), a następnie ''współczynniki Newtona''
+
co znaczy, że <math>b=\sqrt[n]{a}\;</math>, czyli
−
<equation id="eq:4"><math>\begin{matrix}
+
<equation id="eq:6">
−
\left(
+
<math>
−
\begin{matrix}
+
a^\frac{1}{n} = \sqrt[n]{a}.\;
−
n\\k
 
−
\end{matrix}
 
−
\right)
 
−
&=&
 
−
\frac{n(n-1)(n-2)\dots(n-k+1)}{1\cdot 2 \cdot 3 \dots \cdot k}
 
−
\\
 
−
&=& \frac{n!}{k!(n-k)!}
 
−
\end{matrix}\;\;
 
 
</math></equation>
 
</math></equation>
−
zakładamy, że <math>n\;</math> i <math>k\;</math> są to liczby naturalne, oraz <math>n\geq k\;</math>. Mamy:
 
−
<center><math>
 
−
\left(
 
−
\begin{matrix}
 
−
n\\0
 
−
\end{matrix}
 
−
\right) = 1, \;\;\;\;\; \left(\begin{matrix} n\\n \end{matrix}
 
−
\right)=1.
 
−
\;</math></center>
 
  
−
Pokażemy teraz, że <math>\forall\, n, k \in \mathbb N\;</math>, <math>n\geq k\;</math> zachodzi
+
Dowolną potęgę wymierną liczby <math>a\;</math> definiujemy teraz jako
−
<center><math>
+
<equation id="eq:7">
−
\left(
+
<math>a^\frac{p}{n} = (\sqrt[n]{a})^p\; ,
−
\begin{matrix} n\\k\end{matrix}\right)+\left(\begin{matrix}n\\k-1\end{matrix}\right)=\left(\begin{matrix} n+1\\k \end{matrix}
+
</math>
−
\right).\;</math></center>
+
</equation>
 +
gdzie <math>n\in \mathbb N, p\in \mathbb N\;</math>
 +
 
 +
Mamy też: Jeśli <math>a>1\;</math> i <math>b>0\;</math>, to <math>a^b>1 \;</math> i, w konsekwencji, jeśli <math>c_1>c_2\;</math>, to <math>a^{c_1}>a^{c_2}\;</math>. (Dla <math>a<1\;</math> znaki trzeba odwrócić). To pozwala przez ciągłość  zdefiniować <math>a^b\;</math> dla dowolnych <math>a>0\;</math> i <math>b\in \mathbb R\;</math>. Widać też, że funkcja wykładnicza jest '''monotoniczna''' (rosnąca dla <math>a>1\;</math> i malejąca dla <math>a<1\;</math>).
 +
 
 +
 
 +
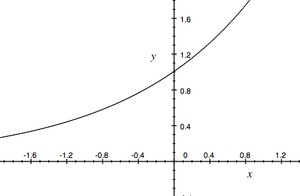
[[file:plus exp.png|thumb|300px|right|Wykres funkcji wykładniczej typu <math>a^x</math>, gdzie a>1]]
 +
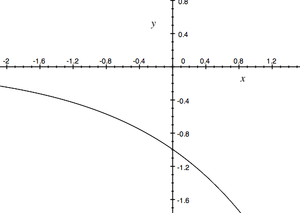
[[file:minus exp.png|thumb|300px|right|Wykres funkcji wykładniczej typu <math>a^x</math>, gdzie a<1]]
  
−
Liczymy bezpośrednio:
+
==Funkcja logarytmiczna==
−
<center><math>
 
−
\left( \begin{matrix}n\\k\end{matrix}\right)+\left(\begin{matrix}n\\k-1 \end{matrix}\right)=\frac{n(n-1)(n-2)\dots(n-k+1)}{1\cdot 2 \cdot 3 \dots \cdot k}+\frac{n(n-1)(n-2)\dots(n-k+2)}{1\cdot 2 \cdot 3 \dots \cdot (k-1)}\cdot\frac{k}{k}
 
−
\;</math></center>
 
  
−
<center><math>
+
Jako że funkcja wykładnicza <math>f(x)=a^x\;</math> jest rosnąca (weźmy, dla ustalenia uwagi, <math>a>1\;</math>) w całej swojej dziedzinie, (dziedziną jest <math>\mathbb R\;</math> a zbiorem wartości <math>\mathbb R_+\;</math>) to istnieje funkcja do niej odwrotna. Zwiemy ją ''logarytmem''.
−
=
 
−
\frac{n(n-1)(n-2)\dots(n-k+2)(n-k+1+k)}{1\cdot 2 \cdot 3 \dots \cdot k} = \left(\begin{matrix} n+1\\k\end{matrix}\right).
 
−
\;</math></center>
 
  
−
Teraz przystępujemy do udowodnienia ''wzoru dwumiennego Newtona'':
+
Zakładamy, że <math>a>0\;</math>, <math>a\ne 1\;</math>.
−
====Twierdzenie====
 
  
−
<math>\forall\, a,b \in \mathbb R\;</math>, <math>\forall\, n\in \mathbb N\;</math> zachodzi <br>
+
'''Def.''' Dla danych <math>a\;</math> oraz <math>y\;</math>, jeśli <math>x\;</math> jest takie, że <math>a^x=y\;</math>, to <math>x\;</math> nazywamy '''logarytmem''' o podstawie <math>a\;</math> z <math>y\;</math> i oznaczamy: <math>x=\log_a y\;</math>. Dziedziną logarytmu jest <math>\mathbb R_+\;</math>, a zbiorem wartości <math>\mathbb R\;</math>.
−
<equation id="eq:5"><math>
 
−
(a+b)^n= a^n + \left(\begin{matrix}n\\1\end{matrix}\right)a^{n-1}b+\left(\begin{matrix} n\\2\end{matrix}\right)a^{n-2}b^2+\dots+\left(\begin{matrix}n\\k\end{matrix}\right) a^{n-k}b^k+\dots
 
−
+\left(\begin{matrix}n\\n\end{matrix}\right)b^n.
 
−
\;</math></equation>
 
  
 +
===Własności===
 +
Mamy więc dla dowolnego <math>a\;</math>: <math>\log_a a = 1\;</math> (ponieważ <math>a^1 = a\;</math>) oraz <math>\log_a 1 = 0\;</math>
  
−
====Uwaga====
+
(ponieważ <math>a^0=1\;</math>).
  
−
Dla <math>n=1\;</math> wzór <xr id="eq:5">(%i)</xr> jest oczywisty. Dla <math>n=2\;</math> i <math>n=3\;</math> wzór wzór <xr id="eq:5">(%i)</xr> powinien być znany ze szkoły średniej (a jeśli nie jest, niech Czytelnik sprawdzi, że <math>(a+b)^2=a^2+2ab+b^2\;</math>; <math>(a+b)^3=a^3+ 3 a^2 b + 3 a b^2 + b^3\;</math>).
+
Własności <xr id="eq:2">(%i)</xr> odpowiada:
  
−
====Dowód====
+
<equation id="eq:8">
−
Tak więc, zgodnie ze schematem dowodu indukcyjnego:
 
−
<ol>
 
−
<li>Teza <math>T_1\;</math> jest prawdziwa.</li>
 
−
<li> Aby pokazać wynikanie <math>T_n\Longrightarrow T_{n+1}\;</math>, weźmy prawą stronę równości <xr id="eq:5">(%i)</xr> dla <math>n+1\;</math>. Mamy <math>(a+b)^{n+1} = (a+b)^n(a+b) = (a+b)^n a + (a+b)^n b, \;</math> i korzystając teraz z założenia o prawdziwości <math>T_n\;</math>, mamy
 
−
<center>
 
−
<math>\begin{matrix} (a+b)^{n+1} =\;a^{n+1} +\left(\begin{matrix}n\\1\end{matrix}\right)a^{n}b+\left(\begin{matrix}n\\2\end{matrix}\right)a^{n-1}b^2+\dots+\left(\begin{matrix}n\\k\end{matrix}\right)a^{n-k+1}b^k+\dots+\left(\begin{matrix}n\\n\end{matrix}\right)a b^n + a^n b +\left(\begin{matrix}n\\1\end{matrix}\right)a^{n-1}b^2+\ldots\\+\left(\begin{matrix}n\\k-1\end{matrix}\right)a^{n-k+1}b^k+\ldots+\left(\begin{matrix}n+1\\n\end{matrix}\right)a b^{n}+b^{n+1}= a^{n+1} +\left(\begin{matrix} n+1\\1\end{matrix}\right) a^{n}b+ \dots+\left(\begin{matrix}n+1\\k\end{matrix}\right) a^{n-k+1}b^k+\dots+\left(\begin{matrix}n+1\\n\end{matrix}\right) a b^n + b^{n+1}\end{matrix},\;</math>
 
−
</center>
 
−
a jest to właśnie lewa strona równości <xr id="eq:5">(%i)</xr> dla <math>n+1\;</math>. Zatem, możemy zakończyć dowód mówiąc, że</li>
 
−
<li> Równość <xr id="eq:5">(%i)</xr> jest prawdziwa dla każdego <math>n\in \mathbb N\;</math>.</li>
 
−
</ol>
 
−
====Uwaga====
 
−
Wzór na dwumian Newtona daje się zapisać o wiele krócej używając symbolu ''sumy'':
 
 
<math>
 
<math>
−
(a+b)^n = \sum^{n}_{k=0} \left(
+
\log_a(b \cdot c) = \log_a b + \log_a c\;\;</math> oraz  <math>\log_a \tfrac{b}{c} = \log_a b - \log_a c\;\;
−
\begin{matrix}
+
</math>
−
n\\k
+
</equation>
−
\end{matrix}
+
 
−
\right)
+
a własności <xr id="eq:3">(%i)</xr>:
−
a^{n-k} b^k
+
<equation id="eq:9">
−
\;</math>
+
<math>\log_a b^c = c\cdot \log_a b\;\;
 +
</math>
 +
</equation>
 +
 
 +
W szczególności: 
 +
<center><math>
 +
\log_a( \sqrt[n]{b}) =\frac{1}{n} \log_a b \;
 +
</math></center>
 +
 
 +
===Przeliczanie logarytmów o różnych podstawach===
 +
 
 +
Często się zdarza, że trzeba przeliczać logarytmy o różnych podstawach. Najbardziej chyba rozpowszechnione są logarytmy '' dziesiętne'' (tzn. o podstawie 10) i '''naturalne''' o podstawie <math>e\approx 2,718...\;</math> (o liczbie <math>e\;</math> powiemy więcej za kilka wykładów).
  
−
Tu symbol: <math>\sum^{n}_{k=0} A_k\;</math> oznacza, że należy  utworzyć sumę <math>n+1\;</math> składników, które powstają z wyrażenia <math>A_k\;</math> przez podstawianie na miejsce <math>k\;</math> kolejno liczb <math>0, 1, 2,\dots, n\;</math>.
+
Jak przeliczać jedne na drugie?
  
−
===Przykład===
+
Rozważmy ogólniejszą sytuację &mdash; logarytmów o dwóch podstawach <math>a\;</math> oraz <math>b\;</math>.
  
−
(startuje się od <math>n_0>1\;</math>) Pokazać, że <math>\forall n>4\;</math> zachodzi <math>2^n>n^2\;</math>.  
+
Wyraźmy teraz <math>\log_ax \;</math> przez <math>\log_b x\;</math>.
  
−
===Przykład===
+
Wyraźmy najsampierw <math>a\;\;</math> jako pewną potęgę <math>b\;\;</math>. Napiszmy: <math>a = b^A\;\;</math> i obustronnie zlogarytmujmy. Mamy: <math>\log_a a = 1 = \log_a (b^A) = A\log_a b\;\;</math>, skąd <math> A=\frac{1}{\log_a b}\;</math>
  
−
(używa się tezy nie tylko <math>T_n\;</math>, ale też  <math>T_{n-1}\;</math> aby pokazać prawdziwość <math>T_{n+1}\;</math>) ''Ciąg Fibonacciego''. Określony jest on rekurencyjnie: <math>F_1 =F_2=1, F_n = F_{n-1} + F_{n-2}\;</math>. Pokazać, że dla dowolnego <math>n\in \mathbb N\;</math> zachodzi
+
Weźmy teraz: <math>y=a^x\;</math>; mamy więc: <math>x=\log_a y\;</math>. Z drugiej strony, <math>\log_b y = \log_b(b^{Ax}) = Ax = \frac{1}{\log_a b} x\;</math> czyli
−
<center><math>
+
<equation id="eq:10">
−
F_n= \frac{1}{\sqrt{5}} \left[ \left(\frac{1+\sqrt{5}}{2}\right)^n - \left(\frac{1-\sqrt{5}}{2}\right)^n \right]
+
<math>\log_a b \log_b y = \log_a y\;\;</math>
−
\;</math></center>
+
</equation>
 +
 
 +
====Przykład====
 +
 
 +
Biorąc <math>a=e\;</math>, <math>b=10\;</math>, mamy: <math>\ln y = \ln 10 \log_{10} y \approx 2,303 \log_{10} y\;</math>.

Aktualna wersja na dzień 11:53, 22 maj 2015


Funkcja wykładnicza

Funkcję wykładniczą definiuje się najsampierw dla wykładników naturalnych. Dla dowolnego [math]a\in \mathbb R \;[/math] oraz [math]n\in \mathbb N \;[/math] można zapisać:

[math]a^n= a\cdot a \dots a \;\;[/math] (n-razy)

Stąd od razu wynika, że:

[math]a^n \cdot a^m = a^{n+m}\;\; [/math]

oraz

[math] \left(a^n\right)^m=a^{n m}\;\; [/math]

Przyjmujemy, że [math]a^0=1\;[/math]. Ujemną potęgę definiujemy rozszerzając zasadę (2) przez dopuszczenie, aby [math]n,m\;[/math] były dowolnymi liczbami całkowitymi. Weźmy: [math] a^{-n} a^n = a^{-n+n}=a^0=1 \;[/math] skąd

[math] a^{-n}=\frac{1}{a^n}\;\; [/math]

(zakładamy tu, że [math]a\ne 0\;[/math]).

Stąd od razu mamy

[math] \left( \frac{a}{b} \right)^n = \frac{a^n}{b^n}\; [/math]

Definiujemy następnie potęgi ułamkowe. Tu zakładamy, że [math]a\gt 0\;[/math] (zaraz się okaże dlaczego).

Oznaczmy: [math]b=a^\frac{1}{n}\;[/math]. Mamy:

[math] b^n = \left( a^\frac{1}{n}\right)^n = a^{\frac{1}{n}\cdot n} = a^1=a \;[/math]

co znaczy, że [math]b=\sqrt[n]{a}\;[/math], czyli

[math] a^\frac{1}{n} = \sqrt[n]{a}.\; [/math]

Dowolną potęgę wymierną liczby [math]a\;[/math] definiujemy teraz jako

[math]a^\frac{p}{n} = (\sqrt[n]{a})^p\; , [/math]

gdzie [math]n\in \mathbb N, p\in \mathbb N\;[/math]

Mamy też: Jeśli [math]a\gt 1\;[/math] i [math]b\gt 0\;[/math], to [math]a^b\gt 1 \;[/math] i, w konsekwencji, jeśli [math]c_1\gt c_2\;[/math], to [math]a^{c_1}\gt a^{c_2}\;[/math]. (Dla [math]a\lt 1\;[/math] znaki trzeba odwrócić). To pozwala przez ciągłość zdefiniować [math]a^b\;[/math] dla dowolnych [math]a\gt 0\;[/math] i [math]b\in \mathbb R\;[/math]. Widać też, że funkcja wykładnicza jest monotoniczna (rosnąca dla [math]a\gt 1\;[/math] i malejąca dla [math]a\lt 1\;[/math]).


Wykres funkcji wykładniczej typu [math]a^x[/math], gdzie a>1
Wykres funkcji wykładniczej typu [math]a^x[/math], gdzie a<1

Funkcja logarytmiczna

Jako że funkcja wykładnicza [math]f(x)=a^x\;[/math] jest rosnąca (weźmy, dla ustalenia uwagi, [math]a\gt 1\;[/math]) w całej swojej dziedzinie, (dziedziną jest [math]\mathbb R\;[/math] a zbiorem wartości [math]\mathbb R_+\;[/math]) to istnieje funkcja do niej odwrotna. Zwiemy ją logarytmem.

Zakładamy, że [math]a\gt 0\;[/math], [math]a\ne 1\;[/math].

Def. Dla danych [math]a\;[/math] oraz [math]y\;[/math], jeśli [math]x\;[/math] jest takie, że [math]a^x=y\;[/math], to [math]x\;[/math] nazywamy logarytmem o podstawie [math]a\;[/math] z [math]y\;[/math] i oznaczamy: [math]x=\log_a y\;[/math]. Dziedziną logarytmu jest [math]\mathbb R_+\;[/math], a zbiorem wartości [math]\mathbb R\;[/math].

Własności

Mamy więc dla dowolnego [math]a\;[/math]: [math]\log_a a = 1\;[/math] (ponieważ [math]a^1 = a\;[/math]) oraz [math]\log_a 1 = 0\;[/math]

(ponieważ [math]a^0=1\;[/math]).

Własności (2) odpowiada:

[math] \log_a(b \cdot c) = \log_a b + \log_a c\;\;[/math] oraz [math]\log_a \tfrac{b}{c} = \log_a b - \log_a c\;\; [/math]

a własności (3):

[math]\log_a b^c = c\cdot \log_a b\;\; [/math]

W szczególności:

[math] \log_a( \sqrt[n]{b}) =\frac{1}{n} \log_a b \; [/math]

Przeliczanie logarytmów o różnych podstawach

Często się zdarza, że trzeba przeliczać logarytmy o różnych podstawach. Najbardziej chyba rozpowszechnione są logarytmy dziesiętne (tzn. o podstawie 10) i naturalne o podstawie [math]e\approx 2,718...\;[/math] (o liczbie [math]e\;[/math] powiemy więcej za kilka wykładów).

Jak przeliczać jedne na drugie?

Rozważmy ogólniejszą sytuację — logarytmów o dwóch podstawach [math]a\;[/math] oraz [math]b\;[/math].

Wyraźmy teraz [math]\log_ax \;[/math] przez [math]\log_b x\;[/math].

Wyraźmy najsampierw [math]a\;\;[/math] jako pewną potęgę [math]b\;\;[/math]. Napiszmy: [math]a = b^A\;\;[/math] i obustronnie zlogarytmujmy. Mamy: [math]\log_a a = 1 = \log_a (b^A) = A\log_a b\;\;[/math], skąd [math] A=\frac{1}{\log_a b}\;[/math]

Weźmy teraz: [math]y=a^x\;[/math]; mamy więc: [math]x=\log_a y\;[/math]. Z drugiej strony, [math]\log_b y = \log_b(b^{Ax}) = Ax = \frac{1}{\log_a b} x\;[/math] czyli

[math]\log_a b \log_b y = \log_a y\;\;[/math]

Przykład

Biorąc [math]a=e\;[/math], [math]b=10\;[/math], mamy: [math]\ln y = \ln 10 \log_{10} y \approx 2,303 \log_{10} y\;[/math].

Źródło: „http://brain.fuw.edu.pl/edu/index.php?title=Funkcja_wykładnicza_i_logarytmiczna&oldid=1140”