TI/Programowanie II/Wprowadzenie do Matlaba: Różnice pomiędzy wersjami
(Utworzono nową stronę "==Wprowadzenie== 200px|thumb|right|Okno powitalne Matlaba Najkrócej można określić Matlab jako pakiet oprogramowania do obliczeń matematy...") |
|||
| (Nie pokazano 4 pośrednich wersji utworzonych przez tego samego użytkownika) | |||
| Linia 1: | Linia 1: | ||
==Wprowadzenie== | ==Wprowadzenie== | ||
| − | + | ||
Najkrócej można określić Matlab jako pakiet oprogramowania do obliczeń matematycznych wyprodukowany w firmie [http://www.mathworks.com/ MathWorks]. Jest to w istocie zintegrowane ''środowisko obliczeniowe'', w którym mamy do dyspozycji: | Najkrócej można określić Matlab jako pakiet oprogramowania do obliczeń matematycznych wyprodukowany w firmie [http://www.mathworks.com/ MathWorks]. Jest to w istocie zintegrowane ''środowisko obliczeniowe'', w którym mamy do dyspozycji: | ||
* własny język programowania wysokiego poziomu, dający możliwość interaktywnego programowania; | * własny język programowania wysokiego poziomu, dający możliwość interaktywnego programowania; | ||
| Linia 423: | Linia 423: | ||
</source> | </source> | ||
| | | | ||
| − | | <source lang=' | + | | <source lang='python'> |
import numpy | import numpy | ||
import pylab | import pylab | ||
| Linia 452: | Linia 452: | ||
plot(x,y);</source> | plot(x,y);</source> | ||
| | | | ||
| − | | <source lang=' | + | | <source lang='python'> |
import numpy as np | import numpy as np | ||
import pylab as p | import pylab as p | ||
| Linia 488: | Linia 488: | ||
</source> | </source> | ||
| | | | ||
| − | | <source lang=' | + | | <source lang='python'> |
import numpy as np | import numpy as np | ||
import pylab as p | import pylab as p | ||
| Linia 509: | Linia 509: | ||
==Ćwiczenia== | ==Ćwiczenia== | ||
| − | + | ====Zadanie 1 ==== | |
[[Plik:Albrecht_Durer_Magic_Square.jpg|300px|thumb|right|<figure id="fig:1"/> Szczegół z miedziorytu Albrechta Durera zatytułowanego Melancholia I, 1514 r.]] | [[Plik:Albrecht_Durer_Magic_Square.jpg|300px|thumb|right|<figure id="fig:1"/> Szczegół z miedziorytu Albrechta Durera zatytułowanego Melancholia I, 1514 r.]] | ||
| Linia 522: | Linia 522: | ||
* Do elementów macierzy można też się odwoływać za pomocą pojedynczego indeksu. W tej sytuacji, macierz odpowiada pojedynczej kolumnie złożonej z kolumn oryginalnej macierzy. Np. dla magicznego kwadratu A(8) odwołuje się do wartości 15 w elemencie macierzy A(4,2). | * Do elementów macierzy można też się odwoływać za pomocą pojedynczego indeksu. W tej sytuacji, macierz odpowiada pojedynczej kolumnie złożonej z kolumn oryginalnej macierzy. Np. dla magicznego kwadratu A(8) odwołuje się do wartości 15 w elemencie macierzy A(4,2). | ||
| − | + | ||
| − | |||
{{Solution|title=Zadanie 2|text= | {{Solution|title=Zadanie 2|text= | ||
Aktualna wersja na dzień 11:05, 23 maj 2015
Spis treści
Wprowadzenie
Najkrócej można określić Matlab jako pakiet oprogramowania do obliczeń matematycznych wyprodukowany w firmie MathWorks. Jest to w istocie zintegrowane środowisko obliczeniowe, w którym mamy do dyspozycji:
- własny język programowania wysokiego poziomu, dający możliwość interaktywnego programowania;
- środowisko zaprojektowane do pracy z macierzami numerycznymi;
- specjalistyczne zestawy procedur obliczeniowych z różnych dziedzin, możliwość zmiany i dodawania własnych funkcji;
- bogate możliwości graficznej prezentacji wyników 2D/3D oraz projektowania własnych interfejsów graficznych (GUI);
- możliwość włączania programów napisanych w innych językach (C, C++, Fortran, Java);
- okienkowo-zorientowane środowiska graficzne do uruchamiania algorytmów na podstawie ich schematów blokowych (np. Simulink);
- wygodne operacje wejścia/wyjścia dla wielu typów danych (np. wav, avi, DICOM)
- zintegrowane interaktywne narzędzia programistyczne: edytor i debugger.
Dzięki tym możliwościom pakiet Matlab (mimo swej relatywnie wysokiej ceny) stał się bardzo popularnym narzędziem obliczeniowym, szczególnie w dziedzinie analizy danych biomedycznych. Pozwala on na dość szybkie pisanie złożonych programów obliczeniowych, pozwalając skupić się na rozwiązywaniu problemu, a nie na samym kodowaniu programu. Warto więc się z nim zapoznać, gdyż jest duża szansa natrafienia na Matlaba w trakcie kariery zawodowej absolwentów naszej specjalności.
Warto również dodać, że osoby nie dysponujące dostępem do Matlaba, chcące zapoznać się z programowaniem w tym języku lub używać posiadane gotowe programy mogą skorzystać z darmowego pakietu GNU Octave. Język Octave jest bardzo podobny do Matlabowego i większość programów może być bez zmian przenoszona między nimi.
Matlab a Python
Ponieważ nasz kurs programowania jest oparty zasadniczo o język Python, właściwe będzie porównanie Pythona i Matlaba. W trakcie nauki programowania w Pythonie, wykorzystywaliśmy interfejs użytkownika, pozwalający nie tylko na uruchamianie programów, ale też na pracę interaktywną. Takim interfejsem jest np. stosowany przez nas idle. W Matlabie podobny interfejs jest wbudowany w program — po uruchomieniu programu dostajemy otwarte okno poleceń.
Jak widać, w obu przypadkach sytuacja jest podobna. Możemy zacząć pracę w sesji interaktywnej wpisując na bieżąco polecenia, które są od razu interpretowane i wykonywane. Wyniki są natychmiast prezentowane na ekranie. Każdy z pakietów daje nam również możliwość napisania programu w osobnym edytorze tekstu, zapisania go na dysku i uruchomienia w dogodnym dla nas momencie.
Podobieństw między Matlabem a Pythonem jest dużo więcej. Oba języki są językami wysokiego poziomu, co oznacza, że dużą część szczegółów implementacji naszego kodu możemy pozostawić w gestii stosowanego pakietu, pisząc programy w sposób bardziej przypominający ogólny algorytm opisany w sposób zrozumiały dla człowieka, a nie dopasowany do konkretnego komputera czy systemu operacyjnego.
Python został zaprojektowany jako język ogólnego stosowania, podczas gdy Matlab był projektowany zasadniczo jako język do obliczeń naukowych. W bardziej zaawansowaną funkcjonalność numeryczną Python został wyposażony dopiero dzięki powstaniu modułów NumPy/SciPy i Matplotlib. Pakiety te wprowadzają do Pythona m. in. wielowymiarowe macierze (numpy.array), operacje na wszystkich elementach macierzy oraz szereg procedur graficznych do prezentacji wyników, używających składni parametrów niezwykle podobnej do tych z Matlaba. Wydaje się więc, że nie powinno być trudności, aby „przesiąść“ się z jednego języka na drugi i sprawnie pisać programy. Tak w dużej mierze jest, są jednak między tymi językami subtelne różnice, które (szczególnie dla początkujących) mogą stanowić pułapkę. Najistotniejsze z tych różnic postaramy się tutaj zaprezentować.
| Matlab | Python (2.x) |
|---|---|
| Podczas pracy interaktywnej Matlab, w odróżnieniu od Pythona, zwraca wartość każdego wyrażenia, które zlecimy mu do wykonania. Wypisywanie wyniku możemy zablokować kończąc wiersz polecenia średnikiem. | Python wykonuje polecenie, ale nie zwraca jego wyniku. Jeśli zależy nam na takim zachowaniu Pythona, możemy zastosować nakładkę IPython, dającą podobną funkcjonalność. |
| Zmienne nie mają konkretnego typu, dopiero po przypisaniu im wartości możemy określić typ zmiennej. | Sytuacja jest podobna. |
Domyślnym typem numerycznym są liczby zmiennoprzecinkowe podwójnej precyzji. Dodatkowo, każda zmienna jest tak naprawdę macierzą zmiennych danego typu, nawet jeśli zawiera tylko jedną wartość (jest wtedy macierzą rozmiaru 1×1).
|
Spośród typów zmiennych numerycznych mamy do dyspozycji liczby całkowite i zmiennoprzecinkowe (które zachowują się inaczej w pewnych operacjach matematycznych). Macierze wprowadzone są przy użyciu pakietu NumPy.
|
Macierze definiujemy z użyciem nawiasów kwadratowych.
|
Macierze definiujemy używając odpowiedniej funkcji
|
Indeksy macierzy piszemy w nawiasach okrągłych.
|
Indeksy macierzy piszemy w nawiasach kwadratowych.
|
| Pierwszy indeks macierzy na numer 1. | Pierwszy indeks macierzy na numer 0. |
Działanie wycinka: elementy liczone od 1, ostatni zawiera się w wycinku.
|
Działanie wycinka: elementy liczone od 0, ostatni element wpisany liczbowo nie zawiera się w wycinku.
|
Łatwe tworzenie wektorów wartości z pewnego zakresu:
|
Łatwe tworzenie wektorów wartości z pewnego zakresu z użyciem pakietu NumPy:
|
| Macierze zachowują wszystkie swoje wymiary. | Macierze mogą zostac „spłaszczone” do wektorów posiadających tylko długość. |
Wymiary macierzy liczą się od lewej do prawej.
|
Wymiary macierzy liczą się od prawej do lewej.
|
Niektóre operatory różnią się od Pythonowych. Niektóre przykłady:
|
Niektóre operatory różnią się od Matlabowych. Niektóre przykłady:
|
Przypisanie zmiennych do siebie powoduje skopiowanie ich zawartości.
|
Przypisanie zmiennych do siebie powoduje wyłącznie powstanie drugiej nazwy tego samego obiektu. Zawartość nie jest kopiowana.
|
Liczby zespolone są wbudowane w działanie pakietu
|
Chcąc użyć liczb zespolonych musimy to explicite zaznaczyć.
ale
|
Niektóre sytuacje wyjątkowe nie powodują przerwania obliczeń, dając użytkownikowi informację o możliwym błędzie w postaci specjalnej wartości.
a także
|
W „czystym” Pythonie użytkownik musi sam zadbać o obsługę wszystkich sytuacji wyjątkowych.
Macierze z modułu NumPy zachowują się podobnie do macierzy Matlaba:
|
Ponieważ każda zmienna numeryczna jest macierzą, podstawowe operatory arytmetyczne opisują działania na macierzach. W szczególności operator mnożenia realizuje mnożenie macierzy:
Aby zrealizować operację osobno dla każdej pary elementów macierzy/wektorów, stosujemy operatory arytmetyczne z kropką (wymiary macierzy muszą być zgodne):
|
Operatory arytmetyczne zastosowane do macierzy wykonują zadane operacje osobno dla wszystkich par elementów tych macierzy. Tak więc w szczególności operator mnożenia w Pythonie odpowiada operatorowi „mnożenia z kropką” w Matlabie i nie realizuje mnożenia macierzowego.
|
Wywołanie pomocy dla obiektu nazwa:
|
Wywołanie pomocy dla obiektu nazwa:
|
| Funkcje matematyczne są wbudowane.
Listę funkcji elementarnych można zobaczyć pisząc:
Bardziej zaawansowane funkcje można zobaczyć pisząc:
|
Funkcje matematyczne są dostępne po załadowaniu modułu NumPy (lub innych,np. math). |
Oczywiście powyższa tabela nie obejmuje wszystkich możliwych różnic, a tylko te najważniejsze, które mogą sprawić kłopot na początku pracy. Nie wydaje się jednak, aby miały one zasadnicze znaczenie dla sprawnego pisania programów w obu omawianych tu językach.
Piszemy program w Matlabie
Z tego co już zostało tutaj powiedziane widzimy, że osoba, która umie napisać program w Pythonie, nie powinna mieć większego kłopotu z napisaniem go również w Matlabie. Należy tylko pamiętać o pewnych różnicach języków i składni, które jednak zasadniczo, po nabyciu pewnej wprawy, nie sprawiają większych trudności.
Aby sprawdzić działanie obu języków w praktyce, napiszemy kilka programów realizujących te same założenia w Pythonie i w Matlabie.
Drobne różnice składniowe
- Pisząc w języku Matlab, warto jest używać wcięć, nie są jednak konieczne. Koniec bloku zaznacza się, pisząc end.
- Nie używamy dwukropków na końcu instrukcji zaczynających blok np. for, czy if.
- Wyrażenie warunkowe:
- if
if a < 30
disp('small')
elseif a < 80
disp('medium')
else
disp('large')
end
- switch
[dayNum, dayString] = weekday(date, 'long', 'en_US');
switch dayString
case 'Monday'
disp('Start of the work week')
case 'Tuesday'
disp('Day 2')
case 'Wednesday'
disp('Day 3')
case 'Thursday'
disp('Day 4')
case 'Friday'
disp('Last day of the work week')
otherwise
disp('Weekend!')
end
- Pętle
- for
for i = 1:m
for j = 1:n
H(i,j) = 1/(i+j);
end
end
Pętla for, tak samo jak w Pythonie, wymaga sekwencji. Sekwencja może być pewnym wektorem. Można też ją utworzyć w następujący sposób:
poczatek:krok:koniec
albo
poczatek:koniec
(wtedy krok = 1). Wynikiem jest wektor wartości od poczatek do koniec o kroku krok. Jest to analog range oraz numpy.arange.
- while
n = 1;
nFactorial = 1;
while nFactorial < 1e100
n = n + 1;
nFactorial = nFactorial * n;
end
- Funkcje
- nagłówek rozpoczyna się słowem function, na przykład:
function [R,E,V]=R_po(t,t_rec,t_in,U_SE,t_mem,R_0,E_0,V_0,t_0,u,dt)
- Zwykle zachowujemy w oddzielnych plikach o nazwie takiej samej, jak funkcja.
Rysujemy wykres funkcji (przykład)
Napiszmy program rysujący wykres funkcji kwadratowej na odcinku od −5 do 5.
| Matlab | Python | |
|---|---|---|
x=linspace(-5,5,11);
y=x.^2;
plot(x,y,'r-');
|
import numpy
import pylab
x=numpy.linspace(-5,5,11)
y=x**2
pylab.plot(x,y,'r-')
pylab.show()
|
Zasadnicze różnice: operator potęgowania, użycie operatora z kropką, konieczność importowania modułów numerycznego i graficznego, osobna procedura do pokazania gotowego wykresu na ekranie.
Narysujmy bardziej dokładnie wykres funkcji sin(x)/x.
| Matlab | Python | |
|---|---|---|
x=linspace(-5,5,101);
y=sin(x)./x;
plot(x,y);
|
import numpy as np
import pylab as p
x=np.linspace(-5,5,101)
y=np.sin(x)/x
p.plot(x,y)
p.show()
|
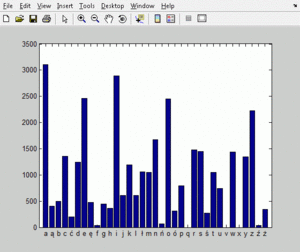
Zliczamy liczbę liter
Narysujmy histogram liczebności poszczególnych liter z pierwszej księgi „Pana Tadeusza” A. Mickiewicza. Tekst znajdziemy tu. Ściągamy plik i zapisujemy w swoim katalogu.
| Matlab | Python | |
|---|---|---|
fid=fopen('PanTadeuszX1.txt','rb');
tekst=fread(fid,'uchar');
fclose(fid);
hist(tekst,min(tekst):max(tekst));
xlim([double('a')-1 double('z')+1]);
set(gca,'XTick',double('a'):double('z'));
set(gca,'XTickLabel',['a':'z']');
|
import numpy as np
import pylab as p
tekst=np.fromfile('PanTadeuszX1.txt','uint8')
p.hist(tekst,max(tekst)-min(tekst)+1)
p.xlim(ord('a')-1,ord('z')+1)
achars=[]
for code in range(ord('a'),ord('z')+1):
achars.append(chr(code))
p.xticks(range(ord('a'),ord('z')+1),achars)
p.show()
|
Wykorzystaliśmy tutaj fakt, że litery alfabetu angielskiego są w kodzie ASCII ułożone bezpośrednio po sobie, alfabetycznie i w kolejności rosnącej. Gdybyśmy w naszym histogramie chcieli uwzględnić również polskie litery, należałoby kolejność słupków histogramu wybrać ręcznie, zgodnie z kolejnością w alfabecie polskim. Histogram musimy utworzyć z wybranych wartości (wysokości słupków) ustawionych w pożądanej kolejności. Dodatkową trudnością jest fakt, że stosowane są różne sposoby kodowania polskich liter (czyli zamiany liter na odpowiadające im wartości liczbowe). Plik tekstowy zastosowany w przykładzie wykorzystuje kodowanie „Windows-1250”, a Matlab domyślnie koduje napisy w standardzie Unicode. Nasz program powinien uwzględniać te fakty.
Ćwiczenia
Zadanie 1
Utwórz w Matlabie macierz z liczbami magicznego kwadratu i policz sumę elementów w każdym wierszu, kolumnie i obu przekątnych. Dodatkowo, możesz policzyć sumę liczb w narożnikach, każdej ćwiartce kwadratu i w czterech środkowych polach.
Wskazówki:
- W Matlabie sumę elementów macierzy zwraca funkcja sum (sprawdź jak ta funkcja działa).
- Transpozycję macierzy A uzyskuje się za pomocą apostrofa tj. A'.
- Elementy na przekątnej macierzy zwraca funkcja diag.
- Odwracanie macierzy z lewa na prawo uzyskuje się za pomocą funkcji fliplr.
- Do elementów macierzy można też się odwoływać za pomocą pojedynczego indeksu. W tej sytuacji, macierz odpowiada pojedynczej kolumnie złożonej z kolumn oryginalnej macierzy. Np. dla magicznego kwadratu A(8) odwołuje się do wartości 15 w elemencie macierzy A(4,2).
Utwórz w Matlabie program, który tworzy macierz z liczbami magicznego kwadratu dla dowolnego n i zwraca sumę elementów w każdym wierszu, kolumnie i obu przekątnych.
Wskazówki:
- W Matlabie kwadrat magiczny można wygenerować funkcją magic.
Napisz funkcję, której dostaje argumenty w postaci sygnału i częstości próbkowania, i przedstawia na rysunkach: dyskretną transformatę Fouriera (wielkość i przesunięcie fazowe), periodogram (kwadrat modułu transformaty Fouriera), gęstość widmową mocy oraz numeryczną weryfikację twierdzenia Parsevala. Następnie wygeneruj sygnał będący sumą dwóch sinusów o częstościach 10 i 40 Hz, długości trwania 2 s i częstości próbkowania 100 Hz i sprawdź działanie funkcji.
Wskazówki:
- W Matlabie dyskretną transformatę Fouriera oblicza funkcja fft.
- Metody szacowania gęstości widmowej mocy można uzyskać pisząc help spectrum.
- Przypomnienie: twierdzenie Parsevala mówi, że całka z gęstości widmowej mocy jest miarą całkowitej energii sygnału. Energię sygnału obliczamy jako sumę kwadratów amplitud sygnału, podzieloną przez jego długość.
Jaka będzie reguła reprezentacji drzewa binarnego za pomocą wektora w językach, w których wektory indeksowane są od 1? Jak zapiszesz reprezentację drzewa z rysunku Figure 3 w języku Matlab?
Wskazówka:
- Proponowany tekst jest zapisany w kodowaniu „Windows-1250”.
- W Matlabie jest dostępna funkcja zamieniająca wybrane kodowanie tekstu na Unicode, na przykład:
- tekst_Unicode = native2unicode(tekst_Win1250,'windows-1250');
- Przypisanie wyniku funkcji hist do jakiejś zmiennej anuluje rysowanie histogramu. W zamian, w zmiennej tej zapisane zostaną obliczone wysokości słupków.
- Kolejność polskiego alfabetu (wzbogaconego o litery dodatkowe „q”, „v” i „x”) to:
- aąbcćdeęfghijklłmnńoópqrsśtuvwxyzźż
- Aby narysować histogram dla wcześniej wyliczonych wysokości słupków użyj funkcji bar.
- Opisy na osi wykresu (ich położenie i tekst) zmienić możemy używając instrukcji:
- set(gca,'XTick',[1 2 3]);
- set(gca,'XTickLabel',['abc']')
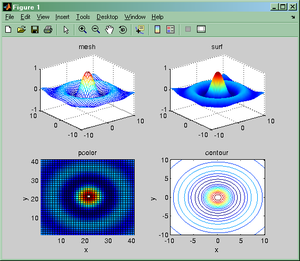
Dlaczego na wykresach brakuje punktu dla r = 0? Co możemy zrobić, aby wykres był kompletny?
Wskazówka:
- Zapoznaj się z działaniem następujących funkcji:
- meshgrid (co zawierają macierze zwracane przez tę funkcję?);
- shading, hidden, colormap;
- subplot, xlabel, ylabel, title.
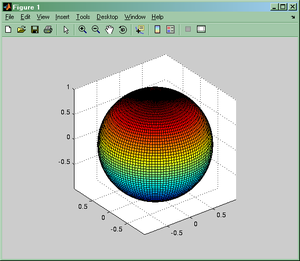
Wskazówka:
- Przypomnij sobie jak opisana jest sfera w sferycznym układzie współrzędnych, a w szczególności jak transformują się współrzędne punktów sfery z układu sferycznego (r,θ,φ) do układu kartezjańskiego (x,y,z).
- Aby kula nie wyglądała jak elipsoida należy skorzystać z polecenia axis equal, które ujednolica rozmiar rysunku wzdłuż osi x, y i z.
Tutaj znajduje się plik zawierający strukturę, która opisuje dekompozycję pewnego sygnału na struktury składowe — „atomy” za pomocą algorytmu MP. Pobierz ten plik, wczytaj do Matlaba i narysuj wynik dekompozycji (wraz ze źródłowymi sygnałami) zawarty w tym pliku. Napisz funkcję rysującą wyniki dla danego kanału i wybranego atomu uwzględniającą informacje zawarte we wczytanej strukturze.
Debugger w Matlabie
Środowisko programowania w Matlabie dostarcza bardzo użytecznego narzędzia pomagającego śledzić działanie programów i niezwykle ułatwiającego wyszukiwanie błędów. Narzędzie to nazywa się z angielska debuggerem (czyli „odrobaczaczem” lub „odpluskwiaczem”).
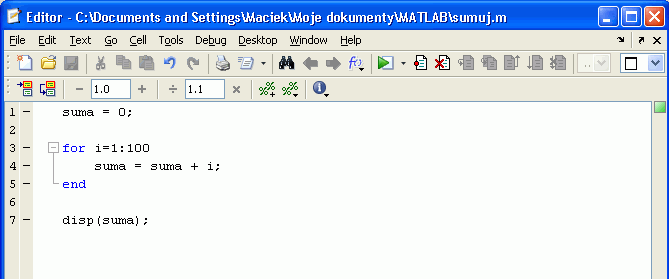
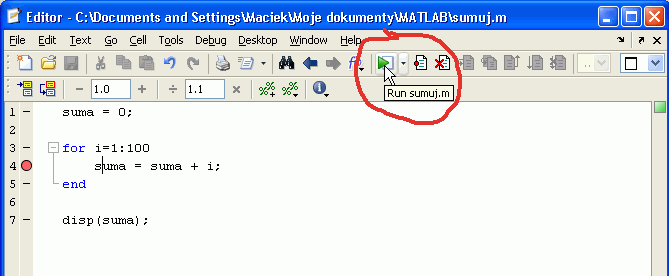
Zasada działania debuggera polega na tym, że możemy zatrzymać wykonujący się program w dowolnym miejscu, nie przerywając wykonania całkowicie, ale tylko chwilowo je wstrzymując. Robimy to przez wcześniejsze wstawienie w tekście programu (który musi być widoczny w oknie Edytora) specjalnych punktów zatrzymania (ang. breakpoints). Pokażemy to na przykładzie prostego programu. Na rysunku poniżej widzimy fragment okna Edytora Matlaba z widocznym interesującym nas fragmentem programu.
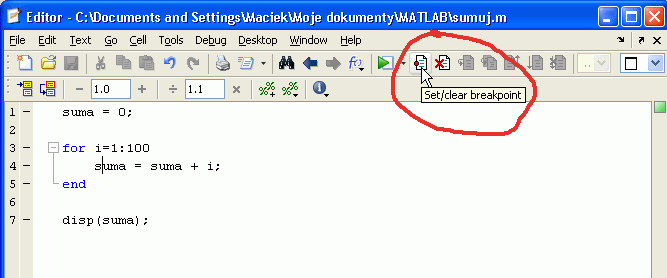
Załóżmy, że chcemy zobaczyć czy pętla w wierszach 3-5 programu prawidłowo sumuje wartości. W tym celu w wierszu 4 umieszczamy punkt zatrzymania, ustawiając kursor w edytorze na tym wierszu i używając guzika z paska poleceń:
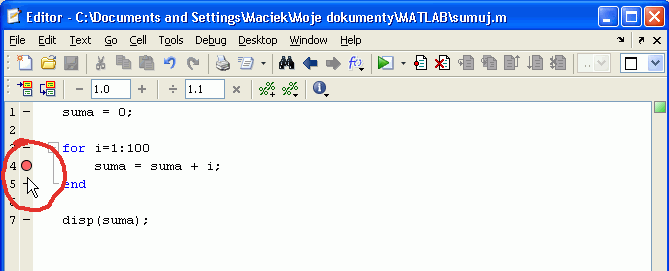
Po naciśnięciu guzika „Set/clear breakpoint” („Ustaw/skasuj punkt zatrzymania”) po lewej stronie wiersza 4 pojawia się czerwona kropka oznaczająca, że w tym miejscu program zostanie wstrzymany.
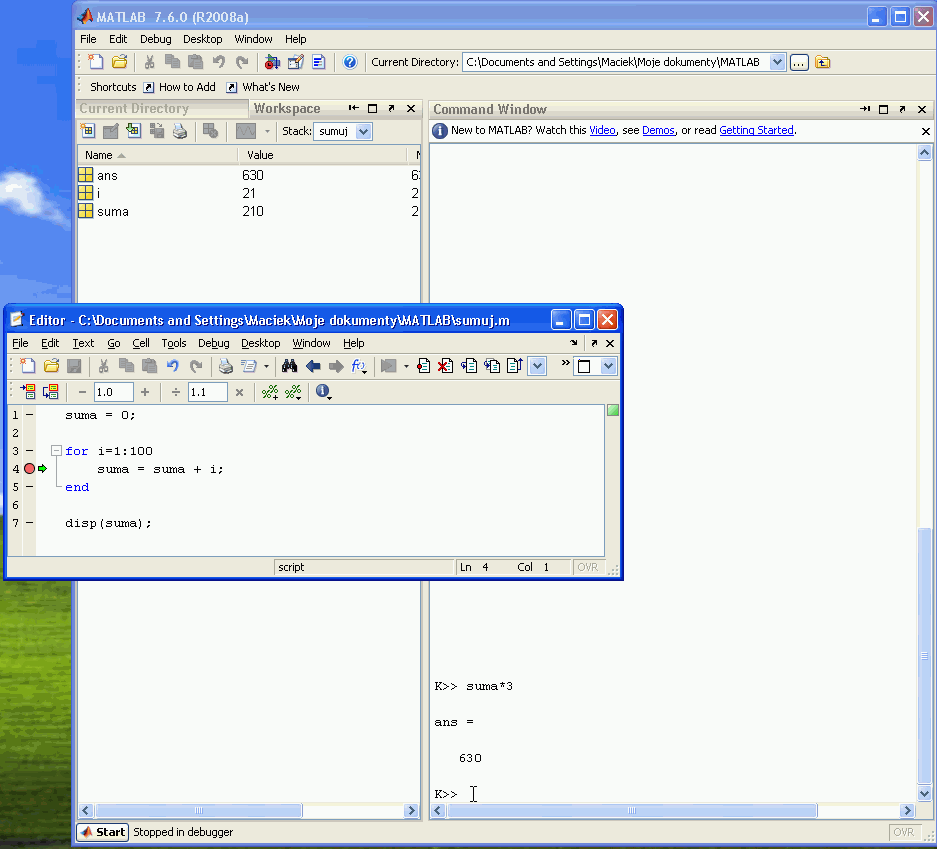
Pozostaje nam teraz uruchomić nasz program. Można to zrobić wpisując odpowiednie polecenie w oknie Poleceń Matlaba (Command window) lub naciskając guzik na pasku poleceń:
Program wykona się aż do napotkania punktu zatrzymania. Wtedy wykonanie zostaje przerwane i w oknie Poleceń zauważymy, że znak zachęty ma dopisaną literę „K”. Zielona strzałka z lewej strony wiersza programu wskazuje jaka komenda programu oczekuje na wykonanie. W oknie Obszar roboczy (Workspace) widzimy wartości wszystkich zmiennych naszego programu, możemy też w oknie Poleceń wpisać dowolne wyrażenie (np. suma*3) i zobaczyć jego wynik. Od tej chwili możemy też wykonywać nasz program krok po kroku naciskając odpowiedni guzik z paska poleceń albo wykonać program do końca (lub następnego punktu zatrzymania).
Informacje dodatkowe
Matlab wyposażony jest w tzw. toolboxy czyli pakiety procedur powiązanych tematycznie do rozwiązywania problemów z jakiejś dziedziny. Pakiety takie można zakupić u producenta (The MathWorks Inc.); aby sprawdzić jakie są aktualnie zainstalowane, wywołujemy polecenie Matlaba ver. W rezultacie dostajemy listę podobną do prezentowanej poniżej.
>> ver ------------------------------------------------------------------------------------- MATLAB Version 7.11.0.584 (R2010b) MATLAB License Number: 123456 Operating System: Microsoft Windows 7 Version 6.1 (Build 7600) Java VM Version: Java 1.6.0_17-b04 with Sun Microsystems Inc. Java HotSpot(TM) Client VM mixed mode ------------------------------------------------------------------------------------- MATLAB Version 7.11 (R2010b) Simulink Version 7.6 (R2010b) Bioinformatics Toolbox Version 3.6 (R2010b) Communications Blockset Version 5.0 (R2010b) Communications Toolbox Version 4.6 (R2010b) Control System Toolbox Version 9.0 (R2010b) Curve Fitting Toolbox Version 3.0 (R2010b) Data Acquisition Toolbox Version 2.17 (R2010b) Database Toolbox Version 3.8 (R2010b) Filter Design Toolbox Version 4.7.1 (R2010b) Financial Toolbox Version 3.8 (R2010b) Fixed-Point Toolbox Version 3.2 (R2010b) Global Optimization Toolbox Version 3.1 (R2010b) Image Acquisition Toolbox Version 4.0 (R2010b) Image Processing Toolbox Version 7.1 (R2010b) Instrument Control Toolbox Version 2.11 (R2010b) MATLAB Builder EX Version 1.3 (R2010b) MATLAB Builder NE Version 3.2 (R2010b) MATLAB Compiler Version 4.14 (R2010b) Mapping Toolbox Version 3.2 (R2010b) Neural Network Toolbox Version 7.0 (R2010b) Optimization Toolbox Version 5.1 (R2010b) Parallel Computing Toolbox Version 5.0 (R2010b) Parallel Computing Toolbox Version 5.0 (R2010b) Partial Differential Equation Toolbox Version 1.0.17 (R2010b) Real-Time Workshop Version 7.6 (R2010b) Robust Control Toolbox Version 3.5 (R2010b) Signal Processing Blockset Version 7.1 (R2010b) Signal Processing Toolbox Version 6.14 (R2010b) Simulink Control Design Version 3.2 (R2010b) Simulink Design Optimization Version 1.2 (R2010b) Simulink Fixed Point Version 6.4 (R2010b) Statistics Toolbox Version 7.4 (R2010b) Symbolic Math Toolbox Version 5.5 (R2010b) System Identification Toolbox Version 7.4.1 (R2010b) Wavelet Toolbox Version 4.6 (R2010b)
Oczywiście możemy sami dopisywać własne procedury, a także korzystać z oprogramowania udostępnionego przez innych twórców. Jako przykład mogą tu posłużyć pakiety do analizy danych biomedycznych EEGLAB czy obrazów MRI SPM rozwijane przez niezależne grupy obejmujące badaczy i programistów. Również procedury Octave-Forge tworzone w ramach projektu GNU Octave mogą współpracować wymiennie z Matlabem.
Python również pozwala na korzystanie z pisanych dla niego pakietów oprogramowania. Musimy je jednak odszukać, ściągnąć i zainstalować sami. W wersji podstawowej będą to:
- python — podstawowy interpreter/kompilator języka Python;
- numpy — biblioteka funkcji matematycznych i obliczeniowych;
- scipy — zestaw bardziej zaawansowanych procedur numerycznych;
- matplotlib — procedury graficzne do sporządzania wykresów i wizualizacji wyników.
- (Uwaga: Mając zainstalowane bilioteki numpy, scipy i matplotlib możemy w programie używać podstawowych funkcji wszystkich tych modułów jedną komendą: import pylab.)
Lista projektów programistycznych w Pythonie obejmuje różnorodne tematy i jest duża szansa znalezienia czegoś dla siebie.
Warto też zwrócić uwagę na pakiet mlabwrap, który pozwala korzystać z Matlaba (musi być zainstalowany w systemie) jakby był on biblioteką Pythona (z pewnymi ograniczeniami, ale wciąż rozwijany).