WnioskowanieStatystyczne/Analiza wariancji: Różnice pomiędzy wersjami
| (Nie pokazano 18 pośrednich wersji utworzonych przez tego samego użytkownika) | |||
| Linia 45: | Linia 45: | ||
==Analiza wariancji ''(ANalysis of VAriance — ANOVA)''== | ==Analiza wariancji ''(ANalysis of VAriance — ANOVA)''== | ||
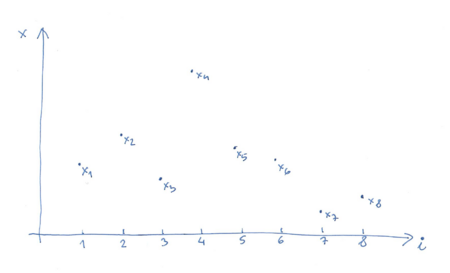
| − | <math>N</math> obserwacji <math>\{x_{i}\}_{i=1..N}</math> | + | <math>N</math> obserwacji <math>\{x_{i}\}_{i=1..N}</math>: |
| − | |||
| − | |||
| − | <math> | + | [[Plik:Anova1.png|center|450px]] |
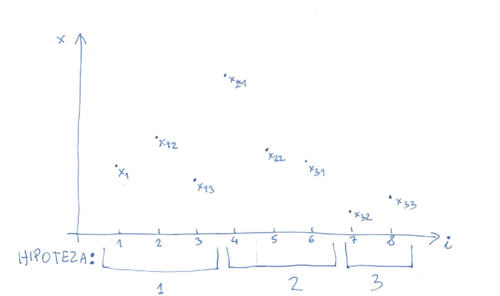
| + | podzielonych na <math>k</math> grup wedle jakiegoś kryterium: | ||
| + | <math>N=n_{1}+n_{2}+...+n_{k}</math>: | ||
| + | [[Plik:Anova2.png|center|500px]] | ||
| + | |||
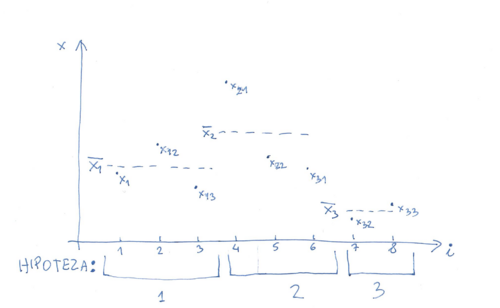
| + | Średnie wewnątrz grup: <math> | ||
\overline{x}_{i}=\frac{1}{n_{i}}\underset{j=1}{\overset{n_{i}}{\sum }}x_{ij} | \overline{x}_{i}=\frac{1}{n_{i}}\underset{j=1}{\overset{n_{i}}{\sum }}x_{ij} | ||
</math> | </math> | ||
| + | [[Plik:Anova3.png|center|500px]] | ||
| + | |||
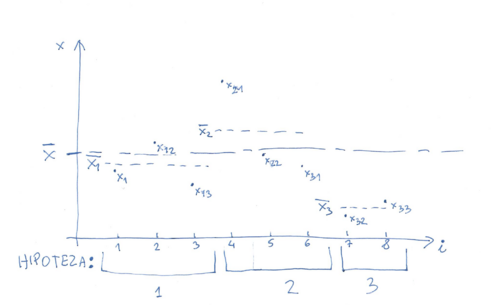
| + | Średnia globalna <math>\overline{x}</math>: | ||
| + | [[Plik:Anova4.png|center|500px]] | ||
| + | |||
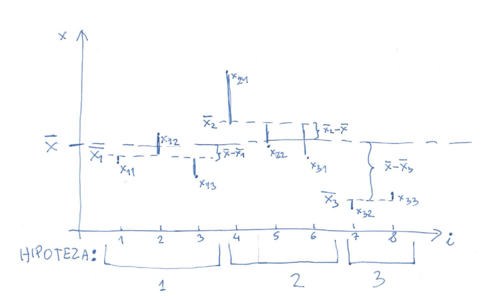
| + | Odchylenia poszczególnych elementów od średnich grup | ||
| + | <math>x_{ij} - \overline{x_i}</math> | ||
| + | oraz odchylenia średnich grup pd średniej globalnej | ||
| + | <math>\overline{x_i} - \overline{x}</math>: | ||
| + | [[Plik:Anova5.png|center|500px]] | ||
| + | |||
| + | ===Rozkład wariancji=== | ||
Rozważmy sumę kwadratów odchyleń wszystkich elementów próby od | Rozważmy sumę kwadratów odchyleń wszystkich elementów próby od | ||
| − | wartości średniej całej próby | + | wartości średniej całej próby |
| − | <math> | + | <math> |
\underset{i=1}{\overset{k}{\sum }}\underset{j=1}{\overset{n_{i}}{\sum }} | \underset{i=1}{\overset{k}{\sum }}\underset{j=1}{\overset{n_{i}}{\sum }} | ||
(x_{ij}-\overline{x})^{2}=\underset{i=1}{\overset{k}{\sum }}\underset{j=1}{ | (x_{ij}-\overline{x})^{2}=\underset{i=1}{\overset{k}{\sum }}\underset{j=1}{ | ||
\overset{n_{i}}{\sum }}(x_{ij}-\overline{x}_{i}+\overline{x}_{i}-\overline{x} | \overset{n_{i}}{\sum }}(x_{ij}-\overline{x}_{i}+\overline{x}_{i}-\overline{x} | ||
| − | )^{2}= | + | )^{2}= |
| − | + | </math> | |
| + | |||
| + | <math> | ||
| + | \underset{i=1}{\overset{k}{\sum }}\underset{j=1}{\overset{n_{i}}{\sum }} | ||
(x_{ij}-\overline{x}_{i})^{2}+\underset{i=1}{\overset{k}{\sum }}\underset{j=1 | (x_{ij}-\overline{x}_{i})^{2}+\underset{i=1}{\overset{k}{\sum }}\underset{j=1 | ||
}{\overset{n_{i}}{\sum }}(\overline{x}_{i}-\overline{x})^{2}+2\underset{i=1}{ | }{\overset{n_{i}}{\sum }}(\overline{x}_{i}-\overline{x})^{2}+2\underset{i=1}{ | ||
\overset{k}{\sum }}\underset{j=1}{\overset{n_{i}}{\sum }}(x_{ij}-\overline{x} | \overset{k}{\sum }}\underset{j=1}{\overset{n_{i}}{\sum }}(x_{ij}-\overline{x} | ||
_{i})(\overline{x}_{i}-\overline{x}) | _{i})(\overline{x}_{i}-\overline{x}) | ||
| − | + | </math> | |
| + | |||
| + | |||
| + | Ponieważ | ||
<math> | <math> | ||
\underset{i=1}{\overset{k}{\sum }}\underset{j=1}{\overset{n_{i}}{\sum }} | \underset{i=1}{\overset{k}{\sum }}\underset{j=1}{\overset{n_{i}}{\sum }} | ||
| Linia 73: | Linia 94: | ||
\overset{k}{\sum }}(\overline{x}_{i}-\overline{x})\underset{j=1}{\overset{ | \overset{k}{\sum }}(\overline{x}_{i}-\overline{x})\underset{j=1}{\overset{ | ||
n_{i}}{\sum }}(x_{ij}-\overline{x}_{i})=0 | n_{i}}{\sum }}(x_{ij}-\overline{x}_{i})=0 | ||
| − | </math> | + | </math>, |
| + | oraz | ||
<math> | <math> | ||
\underset{i=1}{\overset{k}{\sum }}\underset{j=1}{\overset{n_{i}}{\sum }}( | \underset{i=1}{\overset{k}{\sum }}\underset{j=1}{\overset{n_{i}}{\sum }}( | ||
\overline{x}_{i}-\overline{x})^{2}=\underset{i=1}{\overset{k}{\sum }}n_{i}( | \overline{x}_{i}-\overline{x})^{2}=\underset{i=1}{\overset{k}{\sum }}n_{i}( | ||
\overline{x}_{i}-\overline{x})^2 | \overline{x}_{i}-\overline{x})^2 | ||
| − | </math> | + | </math>, |
| + | dostajemy | ||
| + | |||
| + | |||
<math> | <math> | ||
| Linia 86: | Linia 111: | ||
}{\overset{n_{i}}{\sum }}(x_{ij}-\overline{x}_{i})^{2}+\underset{i=1}{ | }{\overset{n_{i}}{\sum }}(x_{ij}-\overline{x}_{i})^{2}+\underset{i=1}{ | ||
\overset{k}{\sum }}n_{i}(\overline{x}_{i}-\overline{x} | \overset{k}{\sum }}n_{i}(\overline{x}_{i}-\overline{x} | ||
| − | ) | + | )^{2} |
</math> | </math> | ||
| + | |||
| + | |||
| + | inaczej | ||
| + | |||
| + | |||
| + | <math>\underset{i=1}{\overset{k}{\sum }}\underset{j=1}{\overset{n_{i}}{\sum }} | ||
| + | (x_{ij}-\overline{x})^{2} = s_{wew}^{2}+s_{pom}^{2} | ||
| + | </math> | ||
| + | |||
Jeśli wszystkie pomiary pochodzą z tej samej populacji o wariancji | Jeśli wszystkie pomiary pochodzą z tej samej populacji o wariancji | ||
| Linia 105: | Linia 139: | ||
podlega rozkładowi <math>F</math> o <math>k-1</math> i | podlega rozkładowi <math>F</math> o <math>k-1</math> i | ||
| − | <math>n-k</math> stopniach swobody. | + | <math>n-k</math> stopniach swobody. |
| + | |||
| + | Wyrażenia | ||
<math> | <math> | ||
\frac{1}{n-k}\underset{i=1}{\overset{k}{\sum | \frac{1}{n-k}\underset{i=1}{\overset{k}{\sum | ||
}}\underset{j=1}{\overset{n_{i} }{\sum | }}\underset{j=1}{\overset{n_{i} }{\sum | ||
| − | }}(x_{ij}-\overline{x}_{i})^{2} | + | }}(x_{ij}-\overline{x}_{i})^{2}</math> |
| + | oraz <math>\frac{1}{k-1}\underset{i=1}{ | ||
\overset{k}{\sum }}n_{i}(\overline{x}_{i}-\overline{x})^{2} | \overset{k}{\sum }}n_{i}(\overline{x}_{i}-\overline{x})^{2} | ||
| − | </math> | + | </math>, czyli |
| − | |||
| − | czyli | ||
| − | |||
<math> | <math> | ||
| − | \frac{s_{wew}^{2}}{n-k} | + | \frac{s_{wew}^{2}}{n-k} |
| − | </math> | + | </math> oraz <math>\frac{s_{pom}^{2}}{k-1} |
| − | + | </math>, są nieobciążonymi estymatami wariancji populacji. | |
| − | są nieobciążonymi estymatami wariancji populacji. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
=Testy par a posteriori= | =Testy par a posteriori= | ||
Testowanie ''a posteriori'' (inaczej ''post hoc'') -> [[WnioskowanieStatystyczne/Bonferroni | porównania wielokrotne]] | Testowanie ''a posteriori'' (inaczej ''post hoc'') -> [[WnioskowanieStatystyczne/Bonferroni | porównania wielokrotne]] | ||
Aktualna wersja na dzień 18:38, 6 maj 2025
Wnioskowanie_Statystyczne_-_wykład
Spis treści
Rozkład F
Niech zmienne [math]x[/math] i [math]y[/math] mają rozkłady [math]\chi ^{2}[/math] o odpowiednio [math]f_{1}[/math] i [math]f_{2}[/math] stopniach swobody. Zmienna
[math] F=\frac{\frac{1}{f_{1}} x}{\frac{1}{f_{2}}y}=\frac{f_{2}x}{f_{1}y} [/math]
posiada rozkład [math]F[/math] z [math]f_{1}[/math] i [math]f_{2}[/math] stopniami swobody o wartości oczekiwanej [math]E(f)=\frac{f_{2}}{(f_{2}-2)}[/math]
[math] f(F)=\left( \frac{f_{1}}{f_{2}}\right) ^{\frac{f_{1}}{2}}\frac{\Gamma \left( \frac{1}{2}\left( f_{1}+f_{2}\right) \right) }{\Gamma \left( \frac{f_{1}}{2} \right) \Gamma \left( \frac{f_{2}}{2}\right) }F^{\frac{f_{2}}{2}-1}\left( 1+ \frac{f_{1}}{f_{2}}F\right) ^{-\frac{f_{1}+f_{2}}{2}} [/math]
Dla próby z rozkładu normalnego wielkość
[math] \chi ^{2}=\underset{i=1}{\overset{N}{\sum }}\frac{(x_{i}-\overline{x})^{2}}{ \sigma ^{2}} [/math]
podlega rozkładowi [math]\chi ^{2}[/math] o [math]f=N-1[/math] stopniach swobody. Jeśli dwie takie próby zostały pobrane z jednej populacji, to iloraz
[math] F=\frac{\left( N_{y}-1\right) \underset{i=1}{\overset{N}{\sum (}}x_{i}- \overline{x})^{2}}{\left( N_{x}-1\right) \underset{i=1}{\overset{N}{\sum }} (y_{i}-\overline{y})^{2}} [/math]
podlega rozkładowi [math]F[/math] o [math]f_{y}[/math] i [math]f_{x}[/math] stopniach swobody.
Analiza wariancji (ANalysis of VAriance — ANOVA)
[math]N[/math] obserwacji [math]\{x_{i}\}_{i=1..N}[/math]:
podzielonych na [math]k[/math] grup wedle jakiegoś kryterium: [math]N=n_{1}+n_{2}+...+n_{k}[/math]:
Średnie wewnątrz grup: [math] \overline{x}_{i}=\frac{1}{n_{i}}\underset{j=1}{\overset{n_{i}}{\sum }}x_{ij} [/math]
Średnia globalna [math]\overline{x}[/math]:
Odchylenia poszczególnych elementów od średnich grup [math]x_{ij} - \overline{x_i}[/math] oraz odchylenia średnich grup pd średniej globalnej [math]\overline{x_i} - \overline{x}[/math]:
Rozkład wariancji
Rozważmy sumę kwadratów odchyleń wszystkich elementów próby od wartości średniej całej próby
[math] \underset{i=1}{\overset{k}{\sum }}\underset{j=1}{\overset{n_{i}}{\sum }} (x_{ij}-\overline{x})^{2}=\underset{i=1}{\overset{k}{\sum }}\underset{j=1}{ \overset{n_{i}}{\sum }}(x_{ij}-\overline{x}_{i}+\overline{x}_{i}-\overline{x} )^{2}= [/math]
[math] \underset{i=1}{\overset{k}{\sum }}\underset{j=1}{\overset{n_{i}}{\sum }} (x_{ij}-\overline{x}_{i})^{2}+\underset{i=1}{\overset{k}{\sum }}\underset{j=1 }{\overset{n_{i}}{\sum }}(\overline{x}_{i}-\overline{x})^{2}+2\underset{i=1}{ \overset{k}{\sum }}\underset{j=1}{\overset{n_{i}}{\sum }}(x_{ij}-\overline{x} _{i})(\overline{x}_{i}-\overline{x}) [/math]
Ponieważ [math] \underset{i=1}{\overset{k}{\sum }}\underset{j=1}{\overset{n_{i}}{\sum }} (x_{ij}-\overline{x}_{i})(\overline{x}_{i}-\overline{x})=\underset{i=1}{ \overset{k}{\sum }}(\overline{x}_{i}-\overline{x})\underset{j=1}{\overset{ n_{i}}{\sum }}(x_{ij}-\overline{x}_{i})=0 [/math],
oraz [math] \underset{i=1}{\overset{k}{\sum }}\underset{j=1}{\overset{n_{i}}{\sum }}( \overline{x}_{i}-\overline{x})^{2}=\underset{i=1}{\overset{k}{\sum }}n_{i}( \overline{x}_{i}-\overline{x})^2 [/math], dostajemy
[math] \underset{i=1}{\overset{k}{\sum }}\underset{j=1}{\overset{n_{i}}{\sum }} (x_{ij}-\overline{x})^{2}=\underset{i=1}{\overset{k}{\sum }}\underset{j=1 }{\overset{n_{i}}{\sum }}(x_{ij}-\overline{x}_{i})^{2}+\underset{i=1}{ \overset{k}{\sum }}n_{i}(\overline{x}_{i}-\overline{x} )^{2} [/math]
inaczej
[math]\underset{i=1}{\overset{k}{\sum }}\underset{j=1}{\overset{n_{i}}{\sum }}
(x_{ij}-\overline{x})^{2} = s_{wew}^{2}+s_{pom}^{2}
[/math]
Jeśli wszystkie pomiary pochodzą z tej samej populacji o wariancji
[math] \sigma ^{2}[/math], to
[math] \frac{s^2_{wew}}{\sigma ^{2}}\ i\ \ \frac{s^2_{pom}}{\sigma ^{2}} [/math]
podlegają rozkładom [math]\chi ^{2}[/math] o odpowiednio [math]n-k[/math] i [math]k-1[/math] stopniach swobody. Iloraz
[math] \frac{\left( n-k\right) s^2_{pom}}{\left( k-1\right) s^2_{wew}} [/math]
podlega rozkładowi [math]F[/math] o [math]k-1[/math] i [math]n-k[/math] stopniach swobody.
Wyrażenia
[math]
\frac{1}{n-k}\underset{i=1}{\overset{k}{\sum
}}\underset{j=1}{\overset{n_{i} }{\sum
}}(x_{ij}-\overline{x}_{i})^{2}[/math]
oraz [math]\frac{1}{k-1}\underset{i=1}{
\overset{k}{\sum }}n_{i}(\overline{x}_{i}-\overline{x})^{2}
[/math], czyli
[math]
\frac{s_{wew}^{2}}{n-k}
[/math] oraz [math]\frac{s_{pom}^{2}}{k-1}
[/math], są nieobciążonymi estymatami wariancji populacji.
Testy par a posteriori
Testowanie a posteriori (inaczej post hoc) -> porównania wielokrotne