TI/Cyfrowy świat

TI/ Analogowy a cyfrowy: sumy kontrolne

Rewolucja cyfrowa rozpoczęła się w drugiej połowie ubiegłego wieku. Dzisiaj zapisywanie i przetwarzanie wszelkiego rodzaju informacji — tekstów, obrazów, wideo i ogólnie danych — w postaci liczb jest dla nas oczywiste, ale nie zawsze tak było. Przejście z tradycyjnego zapisu analogowego na cyfrowy nie jest proste ani oczywiste, ale oferuje zasadniczą korzyść: możliwość wykrywania błędów. Pozwala to na ich korekcję, a w konsekwencji całkowicie bezbłędne przesyłanie i powielanie informacji.

Aby dokładniej zrozumieć ten podstawowy fakt, porównajmy analogowy zapis dźwięku na płycie winylowej z zapisem cyfrowym — na przykład na płycie CD.

CD zapewnia lepszą jakość — to wydaje się oczywiste. Ale, jeśli porównywać CD np. z nową płytą z dobrej tłoczni, odtwarzaną na wysokiej klasy gramofonie, może to już tak oczywiste nie być. No właśnie, nową... Zastanówmy się: płyty CD nie trzeszczą, nawet stare! Czasami nie dadzą się w ogóle odtwarzać, czasami 'gubią' fragmenty na mocno porysowanych płytkach, ale nie trzeszczą! Jak to się dzieje? Kluczem do tajemnicy jest korekcja błędów.

Aby zrozumieć, dlaczego korekcja błędów związana jest ściśle z zapisem cyfrowym, a praktycznie niemożliwa w zapisie analogowym, przyjrzyjmy się bliżej analogowym i cyfrowym zapisom dźwięku.

schemat odtwarzania dźwięku z płyty gramofonowej

Na płycie winylowej (analogowej) dźwięk kodowany jest w ciągłych zmianach głębokości rowka, po którym przemieszcza się igła gramofonu. W przybliżeniu możemy wyobrazić sobie, że 'podskok' igły w większym wgłębieniu rowka powoduje większe wychylenie membrany głośnika (po zamianie w impuls elektryczny i przejściu przez wzmacniacz). Wyżłobienie rowka nowej płyty odwzorowuje więc dokładnie zapisany dźwięk. Zarysowanie lub zabrudzenie wprowadzi przy odtwarzaniu zakłócenia (zwykle trzaski). Jednoznaczne rozróżnienie, które z wyżłobień rowka winylowej płyty odzwierciedlają oryginalny zapis muzyki, a które powstały skutkiem uszkodzeń, jest właściwie niemożliwe, dlatego też muzyka ze starych płyt kojarzy nam się z obecnością trzasków i szumu.

Od góry: ciągły (analogowy) zapis fali dźwiękowej, poniżej próbkowanie, czyli wybór chwil, w których ją mierzymy, dalej zamiana zmierzonych wartości na liczby i liczb na bity. Pasek na dole rysunku może symbolizować na przykład fragment ścieżki na płycie CD: białe pola (zera) odbijają światło lasera, a czarne (jedynki) nie.

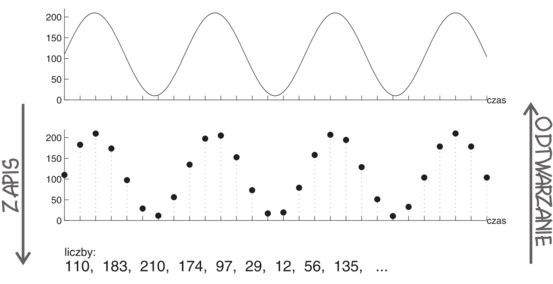
W przypadku zapisu cyfrowego możemy w stosunkowo prosty sposób wykryć wystąpienie zakłóceń, jeśli do zapisu dodamy dodatkową informację. Na płycie CD muzykę zapisujemy jako szereg liczb, oznaczających w uproszczeniu wychylenie membrany głośnika, mierzone w ustalonych odstępach czasu — konkretnie 44100 razy na sekundę. Umówmy się dla przykładu(!), że z każdych dziesięciu kolejnych liczb do zapisu muzyki będziemy wykorzystywać tylko dziewięć, a ostatnią wykorzystamy do zapisania ich sumy. Taki sposób zapisu wprowadza redundancję, czyli nadmiar informacji w zapisie, ponieważ przy prawidłowym odczycie wystarczyłoby znać dziewięć kolejnych liczb, aby szybko obliczyć dziesiątą (ich sumę) — której tak naprawdę przy odtwarzaniu w ogóle nie wykorzystujemy. Jednak jeśli wczytywać będziemy z takiego zapisu wszystkie liczby razem z sumami, po czym niezależnie obliczymy sumę pierwszych dziewięciu licz, i w którejś dziesiątce ostatnia liczba będzie różna od sumy poprzedzających dziewięciu, to mamy pewność, że w tym miejscu wystąpił błąd.

Ta dziesiąta liczba to suma kontrolna; sumy kontrolne (w trochę bardziej wyrafinowanej postaci) stosowane są na przykład w numerach kart kredytowych, numerach kont bankowych, numerach PESEL — pozwala to łatwo i szybko wykryć błąd przy ich wpisywaniu czy przesyłaniu. Informacja o wystąpieniu błędu jest bardzo cenna, również przy odtwarzaniu muzyki:

• Jeśli jesteśmy pewni, że nagły skok natężenia w kilku kolejnych próbkach jest wynikiem błędu zapisu, a nie efektem zamierzonym przez muzyka, to możemy ten skok 'przemilczeć', czyli np. zastąpić 'popsute' próbki średnią wartością poprzednich.
• Po drugie, możemy zwiększyć redundancję jeszcze bardziej i zapisać np. dwie jednakowe kopie. Jeśli uszkodzeniu ulegnie fragment pierwszej kopii, program odtwarzający muzykę może automatycznie sięgnąć do odpowiedniego fragmentu drugiej kopii.

Sumy kontrolne można stosować do sprawdzania poprawności przesyłu informacji w sposób bezpośredni. Na przykład, jeśli ktoś podyktował przez telefon numer PESEL i nie jesteśmy pewni, czy dobrze zapisaliśmy wszystkie liczby, możemy z pierwszych 10 cyfr obliczyć cyfrę kontrolną według ustalonego algorytmu (który znajdziemy na stronie [https://www.gov.pl/web/gov/czym-jest-numer-pesel]) i porówna  z ostatnią z zapisanych cyfr.

Jednak w przypadku np. płyty CD na każdą sekundę muzyki przypada ponad 40 tysięcy liczb, dlatego w praktyce sumy kontrolne obliczają komputery.

OPCJONALNE: próbkowanie i aliasing

Ilustracja twierdzenia Nyquista: jeśli częstości zawarte w sygnale są większe niż połowa częstości próbkowania, występuje aliasing czyli błędny odczyt sygnału cyfrowego.

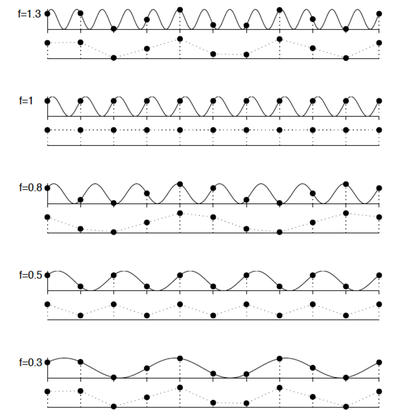
Jak widać, przy przejściu z zapisu analogowego na cyfrowy możemy utracić część informacji — wartości amplitudy 'spomiędzy' próbek oraz dokładność wartości samych amplitud. Ale to jeszcze nie jest najgorsze, co może się przytrafić. Jeśli nie będziemy sygnału próbkować z odpowiednią częstością, może pojawić się aliasing: wyższe częstości nie tylko nie będą widocze w sygnale cyfrowym, ale zafałszują też niższe częstości. Aby uniknąć takiego zniszczenia informacji zawartej w sygnale, musimy stosować twierdzenie Nyquista, które mówi w skrócie, że w próbkowanym sygnale nie może być częstości większych niż połowa częstości próbkowania. Czyli jeśli próbkujemy sygnał z częstością 100 Hz, to musimy upewnić się, że nie ma w nim częstości wyższych niż 50 Hz. Realizowane jest to zwykle przez dolnoprzepustowe filtry antyaliasingowe, usuwające z sygnału wyższe częstości przed próbkowaniem.

Film dostępny w serwisie youtube — pokazuje efekt aliasingu; ten sam efekt obserwujemy na filmach gdy koła dyliżansu kręcę się w "niewłaściwą" stronę. Obraz filmowy próbkowany jest 25 (PAL) lub 30 (NTSC) razy na sekundę.