FT-intuicja: Różnice pomiędzy wersjami
| Linia 2: | Linia 2: | ||
Spróbujmy nabrać potrzebnej na ćwiczeniach intuicji, traktując obliczenia w kategorii iloczynów skalarnych z kolejnymi sinusami o odpowiednio dobranych fazach (w powyższym równaniu fazy są ukryte w kącie liczby zespolonej). Weźmy przykładowy sygnał ''s'' złożony z dwóch sinusów ''a'' i ''b'', ''s'' = ''a'' + ''b'': | Spróbujmy nabrać potrzebnej na ćwiczeniach intuicji, traktując obliczenia w kategorii iloczynów skalarnych z kolejnymi sinusami o odpowiednio dobranych fazach (w powyższym równaniu fazy są ukryte w kącie liczby zespolonej). Weźmy przykładowy sygnał ''s'' złożony z dwóch sinusów ''a'' i ''b'', ''s'' = ''a'' + ''b'': | ||
| − | [[Plik:Ft sig s.png| | + | [[Plik:Ft sig s.png|400px|right|bezramki]] |
| − | [[Plik:Ft sig sa.png| | + | =[[Plik:Ft sig sa.png|400px|right|bezramki]] |
| − | [[Plik:Ft sig sb.png| | + | +[[Plik:Ft sig sb.png|400px|right|bezramki]] |
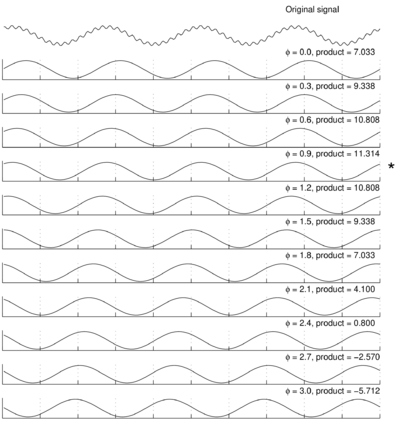
Policzmy iloczyny z sinusami o optymalnie dobranych fazach; jak widać na poniższym rysunku, sinus o częstości 2,4 jest podobny do składowej ''a'' sygnału ''s'', ale miara podobieństwa, czyli wartość [[Wstep#Iloczyn_skalarny|iloczynu skalarnego]], zależy silnie od fazy sinusa, z którym liczymy iloczyn sygnału — gwiazdką oznaczyliśmy fazę, dla której iloczyn jest największy: | Policzmy iloczyny z sinusami o optymalnie dobranych fazach; jak widać na poniższym rysunku, sinus o częstości 2,4 jest podobny do składowej ''a'' sygnału ''s'', ale miara podobieństwa, czyli wartość [[Wstep#Iloczyn_skalarny|iloczynu skalarnego]], zależy silnie od fazy sinusa, z którym liczymy iloczyn sygnału — gwiazdką oznaczyliśmy fazę, dla której iloczyn jest największy: | ||
| − | [[Plik:Ft phase.png| | + | [[Plik:Ft phase.png|400px|center|bezramki]] |
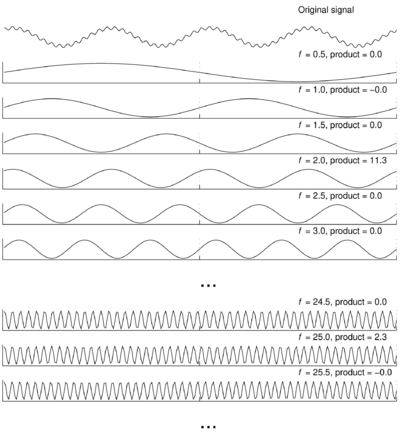
Podobne dopasowania można wykonać dla każdej częstości [[Wstep#Ortogonalność|wzajemnie ortogonalnych]] sinusów o częstościach <math> \frac1T, \frac2T, \ldots</math> do [[Wstep#Aliasing_i_częstość_Nyquista| częstości Nyquista]]. | Podobne dopasowania można wykonać dla każdej częstości [[Wstep#Ortogonalność|wzajemnie ortogonalnych]] sinusów o częstościach <math> \frac1T, \frac2T, \ldots</math> do [[Wstep#Aliasing_i_częstość_Nyquista| częstości Nyquista]]. | ||
| − | [[Plik:Ft freq.png| | + | [[Plik:Ft freq.png|400px|center|bezramki]] |
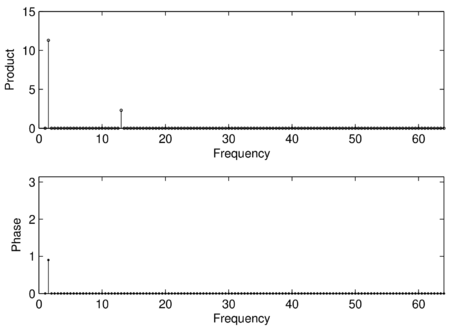
Wyniki — optymalne fazy i uzyskane dla nich maksymalne wartości iloczynów skalarnych — przedstawiamy na wykresach: | Wyniki — optymalne fazy i uzyskane dla nich maksymalne wartości iloczynów skalarnych — przedstawiamy na wykresach: | ||
[[Plik:Fake spect.png|450px|center|bezramki]] | [[Plik:Fake spect.png|450px|center|bezramki]] | ||
Wersja z 17:49, 2 wrz 2024
Intuicyjna intepretacja przekształcenia Fouriera
Spróbujmy nabrać potrzebnej na ćwiczeniach intuicji, traktując obliczenia w kategorii iloczynów skalarnych z kolejnymi sinusami o odpowiednio dobranych fazach (w powyższym równaniu fazy są ukryte w kącie liczby zespolonej). Weźmy przykładowy sygnał s złożony z dwóch sinusów a i b, s = a + b:
=
+
Policzmy iloczyny z sinusami o optymalnie dobranych fazach; jak widać na poniższym rysunku, sinus o częstości 2,4 jest podobny do składowej a sygnału s, ale miara podobieństwa, czyli wartość iloczynu skalarnego, zależy silnie od fazy sinusa, z którym liczymy iloczyn sygnału — gwiazdką oznaczyliśmy fazę, dla której iloczyn jest największy:
Podobne dopasowania można wykonać dla każdej częstości wzajemnie ortogonalnych sinusów o częstościach [math] \frac1T, \frac2T, \ldots[/math] do częstości Nyquista.
Wyniki — optymalne fazy i uzyskane dla nich maksymalne wartości iloczynów skalarnych — przedstawiamy na wykresach: