Pracownia EEG 2/Potencjały wywołane: Różnice pomiędzy wersjami
| Linia 174: | Linia 174: | ||
Musimy przeprowadzić test statystyczny. Możemy skonstruować go np. tak: | Musimy przeprowadzić test statystyczny. Możemy skonstruować go np. tak: | ||
| − | Mamy dwa warunki I i II. Jako statystykę przyjmiemy różnicę pomiędzy amplitudą | + | Mamy dwa warunki I i II. Jako statystykę przyjmiemy różnicę pomiędzy amplitudą zmierzoną w warunku II (A<sub>II</sub>) a amplitudą zmierzoną w warunku I (A<sub>I</sub>): |
| − | : ''S'' = | + | : ''S'' = A<sub>II</sub> − A<sub>I</sub> |
Postawmy hipotezę zerową, że nie ma różnicy w amplitudzie pomiędzy warunkiem II a I oraz hipotezę alternatywną, że różnica taka występuje. | Postawmy hipotezę zerową, że nie ma różnicy w amplitudzie pomiędzy warunkiem II a I oraz hipotezę alternatywną, że różnica taka występuje. | ||
: H<sub>0</sub>: ''S'' = 0 | : H<sub>0</sub>: ''S'' = 0 | ||
Wersja z 14:01, 23 paź 2024
Pracownia EEG 2 / Potencjały wywołane
Spis treści
Wstęp
Potencjały wywołane
Wstęp
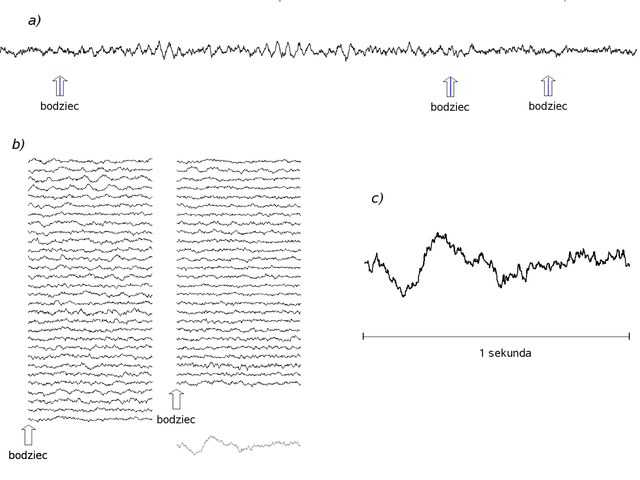
Potencjały wywołane EEG (ang. evoked potentials, EP) są śladami odpowiedzi mózgu na bodźce. W przypadku MEG poprawnie mówi się o polach wywołanych (ang. evoked fields, EF). Zwykle reakcja ta jest mała (wyjątek stanowią kompleksy K) i w zapisie pojedynczej realizacji reakcji na bodziec najczęściej niewidoczna wśród czynności pochodzącej od wielu innych procesów zachodzących w tym samym czasie w mózgu. Ich wyodrębnienie z tak zwanego tła EEG/MEG, czyli manifestacji elektrycznej innych, trwających w tym samym czasie w mózgu procesów (aktywny prąd niezależny), wymaga w dniu dzisiejszym zapisu odpowiedzi na szereg powtórzeń tego samego bodźca (rys. 1). Pierwsze potencjały wywołane pokazał pod koniec lat 40-tych Dawson (Dawson, 1947) wykonując superpozycję pojedynczych realizacji na kliszy fotograficznej. Z czasem skomplikowane urządzenia analogowe zastąpione zostały przez cyfrowe uśrednianie kolejnych fragmentów EEG, zsynchronizowanych według momentu wystąpienia bodźca, łatwo realizowane za pomocą komputera.
Techniki te opierają się na założeniu, że zawarta w EEG odpowiedź mózgu na każdy z kolejnych bodźców jest niezmienna, a EEG odzwierciedlające pozostałe procesy traktowane jest jak nieskorelowany z nią proces stochastyczny. Zależnie od rodzaju potencjałów wywołanych, założenia te są mniej lub bardziej nieuzasadnione; podważa je choćby powszechnie znany efekt habituacji, polegający na osłabieniu późnych potencjałów wywołanych kolejnymi powtórzeniami bodźca.
Istota potencjałów wywołanych jest przedmiotem otwartej dyskusji i dziesiątków prac, dotykających od lat podstawowych w tej dziedzinie pytań: czym jest potencjał wywołany, który widzimy w uśrednionym przebiegu? Czy naprawdę wynika z deterministycznie powtarzanej, jednakowej odpowiedzi pojawiającej się po każdym powtórzeniu bodźca niezależnie od „tła”, czy może wynika z reorganizacji faz tego właśnie „tła” EEG, czy może kombinacji tych dwóch efektów? Jest to wspaniałe pole dla zastosowań zaawansowanych metod modelowania i analizy sygnałów. W ostatnich latach powstają dziesiątki prac na ten temat, a od czasu do czasu również krytyczne artykuły wykazujące, że dotychczasowe odkrycia są raczej artefaktami stosowanych metod a nie wynikają z własności analizowanych danych (Yeung et al., 2004). Jak widać jest tu wciąż bardzo wiele do zrobienia, gdyż zrozumienie tego mechanizmu stoi na drodze do „świętego Graala”, którym w tej dziedzinie jest wyodrębnienie pojedynczych potencjałów wywołanych.
Niezależnie od tego, w neurofizjologii klinicznej nazwą potencjał wywołany określa się krzywą widoczną po uśrednieniu odpowiedzi na kilkanaście do kilku tysięcy bodźców (Szelenberger 2000). Gromadzona od dziesięcioleci wiedza o behawioralnych i klinicznych korelatach potencjałów wywołanych opiera się na rozpoznawaniu w przebiegach uśrednionych tak zwanych załamków, czyli przejściowych wzrostów lub spadków potencjału (na przykład na rys. 1 widać załamek P300). Nazwy załamków składają się zwykle z litery „P” (od ang. positive), jeśli wychylenie jest dodatnie, lub „N” (od ang. negative), jeśli wychylenie jest ujemne, oraz liczby. Uwaga:
- Nie ma niestety jednej ustalonej konwencji prezentacji potencjałów koniecznie trzeba więc zwracać uwagę na orientację wykresu, a wykonując wykres samemu - zamieszczać informację o orientacji kierunku dodatniego,gdyż kierunek dodatni może być wykresie skierowany do góry lub do dołu.
- Liczba następująca po N lub P określa przybliżoną liczbę milisekund od wystąpienia bodźca, czyli tak zwaną latencję. Nie można jednak ścisłego związku między tą liczbą a liczbą milisekund np. potencjał P300 w zależności od szczegółów paradygmatu doświadczalnego może wystąpić znacznie później. np. w eksperymentach językowych zdarza się że P300 występuje później niż N400 :-).
Rys. 2 przedstawia schematycznie najważniejsze załamki rozpoznawane w potencjałach słuchowych, czyli wywoływanych bodźcem dźwiękowym. Dla potencjałów wzrokowych i somatosensorycznych istnieją podobne klasyfikacje.
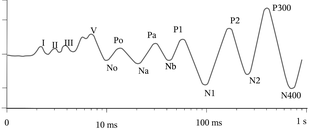
Najszybsze (czyli o najmniejszej latencji) składowe to potencjały egzogenne, odzwierciedlające wstępne fazy przetwarzania informacji. W potencjałach słuchowych są to potencjały pnia (ang. brainstem auditory evoked potentials, BAEP), składające się z siedmiu fal występujących pomiędzy 1 a 12 ms od bodźca. Są one generowane np. w nerwie słuchowym czy pniu mózgu, i wykorzystywane w klinicznej diagnostyce integralności dróg słuchowych. Podobnie jak inne wczesne potencjały o latencjach poniżej 100 ms, są praktycznie niezależne od stanu uwagi.
Po potencjałach o średniej latencji (między 12 a 50 ms) zaczynają się późne potencjały słuchowe (od 100 ms od podania bodźca), odzwierciedlające bardziej złożone reakcje na bodziec. Potencjały ok. 100 ms obserwowane w okolicach sensorycznych odzwierciedlają odpowiedź tejże kory na bodziec. Ich amplituda zależy od parametrów fizycznych bodźca oraz od uwagi, np. amplituda załamka N100 wzrasta w stanie skupienia uwagi czy pobudzenia emocjonalnego. Pierwszy i najpopularniejszy całkowicie endogenny załamek to P300, pojawiający się po rozpoznaniu bodźca oczekiwanego, na którym skupiamy uwagę: na przykład, jeśli w serii pojawiających się losowo liter mamy zliczać wystąpienia jednej z nich, to na średniej odpowiedzi na pojawienie się tej litery pojawi się załamek P300. Załamek ten występuje również w odpowiedzi na bodźce wyczekiwane, niespodziewane i ważne dla osoby (np. własne imię).
Uśrednianie w dziedzinie czasu
Jak już było wspomniane powyżej podstawową techniką stosowaną do analizy potencjałów wywołanych jest uśrednianie wielu realizacji odpowiedzi na bodziec wyrównanych względem jakiegoś charakterystycznego zdarzenia, np. momentu podania bodźca albo momentu behawioralnej reakcji na bodziec (np. wciśnięcie przycisku). Podejście to bazuje na trzech założeniach:
- Reakcja jest czasowo związana z bodźcem. Tzn. w kolejnych realizacjach występuje ona zawsze z tym samym opóźnieniem.
- Reakcja na bodziec skutkuje zawsze pojawieniem się w sygnale składowej o stałym kształcie (mówimy o stałej morfologii).
- Spontaniczna czynność EEG — ta która nie dotyczy przetwarzania interesującego nas bodźca — jest niezależnym, stacjonarnym szumem o średniej zero.
Zgodnie z powyższymi założeniami mierzony w i-tej realizacji sygnał można wyrazić jako:
- [math]x_i(t) = s(t) + n_i(t)[/math]
Uśrednianie po N realizacjach daje:
- [math]\bar x (t) = \frac{1}{N} \sum_{i=1}^N x_i(t) = \frac{1}{N} \left(N s(t) + \sum_{i=1}^N n_i(t) \right) [/math]
Wartość oczekiwana średniego sygnału wynosi:
- [math]\mathrm{E}\left[ \bar x(t) \right] = s(t) [/math]
gdyż dla szumu o średniej zero mamy:
- [math]\mathrm{E}\left[\frac{1}{N} \sum_{i=1}^N n_i(t)\right] = 0[/math].
Wariancja [math]\bar x(t)[/math] wynosi:
- [math]\sigma^2_{\bar x(t)} = \mathrm{E} \left[ \left( \frac{1}{N} \sum_{i=1}^N n_i(t)\right)^2 \right] \approx \frac{1}{N} \sigma^2_{n(t)}[/math]
gdyż [math]s(t)[/math] jest deterministyczne.
Dla potencjałów pojawiających się w pierwszych kilkudziesięciu milisekundach po bodźcu model ten można uznać za poprawny, gdyż wykazują one zależność głównie od parametrów fizycznych bodźca. Dla późniejszych składowych staje się on coraz bardziej wątpliwy ze względu na występujące korelacje ze stanem (np. uwagi) badanego.
Dla późniejszych składowych można by postulować bardziej ogólną wersję modelu potencjału wywołanego:
- [math]x_i(t) = s_i(t) + n_i(t)[/math]
Ten model uwidacznia, że do opisu potencjału wywołanego potrzebna jest nie tylko średnia, ale i wyższe momenty rozkładu (np. drugi moment centralny czyli wariancja).
Wariancja w przypadku szumu skorelowanego
W poprzednim paragrafie pokazaliśmy, że w przypadku niezależnego szumu wariancja uśrednionego sygnału (w danej chwili czasu) maleje jak [math]\frac{1}{N}[/math]. Jednak w przypadku gdy kolejne próbki szumu są skorelowane (np. występuje silna aktywność rytmiczna alfa) sytuacja się komplikuje. Intuicyjnie łatwo możemy to sobie wyobrazić w granicznym przypadku. Załóżmy, że tło dla potencjałów o stałej morfologii stanowi sinusoida. Jeśli będziemy podawać bodźce w odstępach będących wielokrotnością okresu tej sinusoidy to w uśrednianych fragmentach sygnału owa sinusoida jest tak samo powtarzalna jak badany potencjał i uśrednianie nie prowadzi do poprawy stosunku amplitudy sygnału do amplitudy tła.
Stopień zależności pomiędzy próbkami można zmierzyć przy pomocy funkcji autokorelacji. Jeśli funkcję autokorelacji przybliżymy przez:
- [math]R_{xx}(\tau) = \sigma^2 \exp(-\beta |\tau|) \cos(2 \pi f_0 \tau)[/math]
gdzie [math]\sigma^2[/math] jest wariancją szumu, [math]f_0[/math] jest średnią częstością aktywności rytmicznej, [math]\beta/ \pi[/math] jest szerokością pasma tej czynności, zaś [math]\tau[/math] opóźnieniem, to wariancję potencjału wywołanego można wyrazić jako:
- [math]\sigma^2_{\bar x(t)} = \frac{\sigma^2}{N} \left[ \frac{1-\exp(-2 \beta T)}{1 - 2 \exp(- \beta T) \cos(2 \pi f_0 T) +\exp(-2 \beta T)} \right] [/math]
gdzie [math]T[/math] jest odstępem między bodźcami. Widać stąd, że obecność czynności rytmicznej w tle wpływa na stosunek sygnału do szumu. Z powyższego równania widać, że stosunek wariancji dąży do [math]\frac{\sigma^2}{N}[/math] gdy [math]\beta T[/math] staje się duże.
Periodyczna stymulacja może ponadto prowadzić do wzbudzenia czynności rytmicznej o częstości równej częstości pobudzania bądź jej harmonicznej.
Wariancja latencji
Jedną z form zmienności potencjału wywołanego w pojedynczych realizacjach jest wariancja latencji.
# -*- coding: utf-8 -*-
Zmienność latencji prowadzi do:
- zmniejszenia amplitudy [math]\bar x[/math]
- wzrostu rozciągłości czasowej załamka
O tych konsekwencjach zmienności latencji należy w szczególności pamiętać porównując średnie potencjały uzyskane w różnych warunkach eksperymentalnych. Gdy zauważymy, że średnie potencjały różnią się amplitudą należy rozważyć możliwość, że w istocie warunki eksperymentalne wpływają na różnice w wariancji latencji.
Naturalne jest, że zmienność latencji jest bardziej widoczna w przypadku załamków trwających krótko niż w przypadku załamków trwających długo. Wariancja latencji rożnie wraz z jej wartością, stąd wśród późnych składowych potencjałów wywołanych nie obserwuje się komponentów krótkotrwałych.
Habituacja
Zmienność w odpowiedziach na kolejno występujące po sobie bodźce można podzielić na komponent stochastyczny i deterministyczny. Komponent deterministyczny odzwierciedla zmianę czułości układu nerwowego na kolejne bodźce. Nowy bodziec często wywołuje reakcje pobudzenia widoczną w wielu parametrach takich jak przewodnictwo skóry, rytm serca i reaktywność kory mózgowej. Powszechnie obserwowanym zjawiskiem jest spadek reaktywności na powtarzające się bodźce zwany habituacją. Niekiedy obserwuje się także zjawisko przeciwne — wzrost reaktywności na bodziec — zwane sensytyzacją.
Klasycznym sposobem na badanie tych zjawisk w potencjałach wywołanych jest uśrednianie w podzbiorach lub uśrednianie blokowe. Wymaga ono zmiany paradygmatu rejestracji danych. Załóżmy, że interesującym nas bodźcem jest błysk światła. Chcemy zaobserwować ewentualne zmiany amplitudy i latencji w ciągu 100 potencjałów będących reakcją na błysk powtarzający się co 500 ms.
Uśrednianie w podzbiorach
W metodzie tej musimy założyć, że proces habituacji jest powolny, tzn. zmiany pomiędzy kolejnymi reakcjami są bardzo małe. W takim przypadku możemy podzielić długą serię bodźców na ciąg pod-serii i uśrednienie przeprowadzić dla każdej pod-serii osobno.
Uśrednianie blokowe
W tym celu eksperyment wykonujemy w wielu seriach. Jedna seria składa się ze 100 błysków powtarzanych co 500 ms. Po serii następuje przerwa trwająca np. 5 s (długość przerwy wyraża nasze oszacowanie czasu potrzebnego na zanik habituacji). Po przerwie seria jest powtarzana. Powtórzeń serii wykonujemy N. Następnie uśredniamy fragmenty sygnałów odpowiadające sobie w kolejnych seriach.
W tym paradygmacie zakładamy, że każda seria rejestrowana jest w tych samych warunkach. Zaniedbujemy efekty związane ze zmęczeniem i zmianami w np. stopniu koncentracji badanego.
Załamki w krzywej potencjału wywołanego vs ukryte komponenty
Komponenta potencjału wywołanego to bardzo ważne ale jednocześnie źle określone pojęcie. Krzywa otrzymana w wyniku uśredniania potencjałów wywołanych przedstawia serię załamków dodatnich i ujemnych, ale trzeba być świadomym, że ten przebieg napięcia rejestrowany przez elektrody przedstawia tak naprawdę sumę potencjałów pochodzących od wielu dość niezależnie działających źródeł w mózgu. Przyczynek pochodzący od jednego funkcjonalnego źródła będziemy określać jako komponentę.
Komentarza wymaga też pojęcie źródła funkcjonalnego. Czynność elektryczną synchronicznie działających neuronów piramidalnych w określonym fragmencie kory mózgowej z pewnej odległości można przybliżyć potencjałem dipola prądowego. Taki aktywny fragment kory stanowi źródło dające przyczynek do mierzonego na powierzchni głowy potencjału. W najprostszej sytuacji taki przyczynek może być obserwowany jako komponenta. Mózg jest jednak obiektem niezwykle złożonym i gęsto połączonym. Wiele obszarów korowych może być funkcjonalnie połączonych i aktywowanych synchronicznie w celu realizacji określonego zadania — o takim funkcjonalnym zespole też możemy myśleć jako o pojedynczym źródle, choć może ono mieć złożoną strukturę przestrzenną. Często zatem myślimy o komponentach ukrytych potencjału wywołanego jako o aktywności takich funkcjonalnych zespołów.
Po tym wstępie widać już chyba, że do zrozumienia co dzieje się w czasie reakcji na bodziec, którą obserwujemy w potencjale wywołanym, bardziej pożądane byłoby badanie komponent ukrytych niż poszczególnych załamków krzywej potencjału wywołanego, która stanowi ważoną sumę owych komponentów. Zanim przejdziemy do omówienia technik służących „wyłuskiwaniu” komponent prześledźmy kilka symulacji i wnioski z nich płynące.
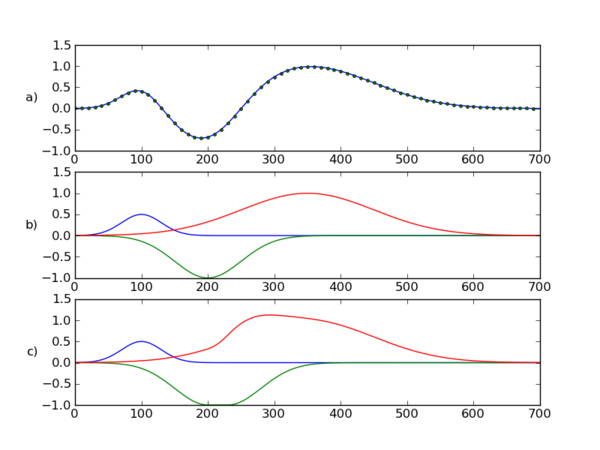
Załamki i komponenty nie są tym samym.
Tę samą krzywą można otrzymać na nieskończenie wiele sposobów przez sumowanie rożnych kombinacji domniemanych komponentów. Przykładowy rysunek pokazuje, jak tę samą krzywą można złożyć z dwóch rożnych zestawów komponentów (kod wytwarzający przykładową symulację pokazany jest poniżej).
ICA
Popularna w ostatnich latach metoda "czyszczenia" sygnału z artefaktów opiera się na analizie składowych niezależnych.
Analiza składowych niezależnych (ang. Independent Components Analysis, ICA) to jedno z określeń dla metod rozwiązywania problemu tzw. ślepej separacji źródeł (blind source separation, BSS). Przyjęty model zakłada, że mamy do czynienia z następującą sytuacją: dane którymi dysponujemy ([math]\vec{x}[/math] — np. zapisy z kilku mikrofonów) są liniową mieszaniną kilku statystycznie niezależnych sygnałów ([math]\vec{s}[/math] — np. głosy kilku mówiących jednocześnie osób, tzw. cocktail party problem):
[math] \vec{x} = A \vec{s} [/math]
[math]A[/math] zwiemy macierzą mieszającą, a rozwiązania szukamy w postaci macierzy separującej [math]B[/math], takiej, że wektor sygnałów
[math] \vec{y}=B\vec{x} [/math]
jest możliwie bliski (nieznanym) sygnałom [math]\vec{s}[/math]. Wymóg niezależności statystycznej elementów [math]\vec{y}[/math] wymaga uwzględnienia statystyk rzędów wyższych niż 2, czyli korelacji (używanych w PCA). Przetwarzanie wstępne polega często na wyzerowaniu statystyk do rzędu 2, czy odjęciu średniej i obrocie diagonalizującym macierz kowariancji (zwykle PCA). Uzyskanie w prosty sposób dekorelacji ułatwia działanie procedur realizujących dalsze wymagania niezależności. Realizowane są one zwykle z pomocą sztucznych sieci neuronowych o specjalnie dobieranych regułach uczenia.
Procedura usuwania artefaktów polega na zerowaniu komponentów, które zidentyfikujemy -- na przykład na podstawie kształtu, widma i rozkładu przestrzennego -- i odtwarzaniu sygnału z pominięciem tych komponentów. Procedura jest zaimplementowania w programie Svarog, którego aktualną wersję można ściągnąć stąd: https://braintech.pl/software/svarog-streamer/
Zadanie 1: Rejestracja i analiza potencjałów związanych ze zdarzeniem
Eksperyment 1. Obserwacja bodźca wzrokowego
Rejestracja
- Paradygmat: badany słucha przez słuchawki serii dźwieków. Bodźce trwają 100 ms i powtarzają się co losową wartość 0.7 - 1.2s sekundy. W ramach badania mają być podawane dwa bodźce, które będą róznić się wysokością dźwięku (np. C i G). Bodźce mają pojawiać się w proporcji 1:6 w dwóch blokach: dany dźwięk w jednym bloku jest bodźcem rzadkim, w drugim czestym, na początku bloku powinien pojawić się częsty bodzieć min. 15 razy. Pomiędzy blokami powinna być przerwa, której długość reguluje badany. Zadanie poprzedza krótka instrukcja, a kończy podziękowanie.
- Pomiar
- Zakładamy czepek i elektrody w systemie 10-20, dbamy o to by opory pomiędzy elektrodami były poniżej 10 kΩ i różnice pomiędzy oporami różnych elektrod nie przekraczały 20%.
- Elektrodę GND mocujemy w otworze czepka odpowiadającym pozycji AFz (na linii centralnej 10% w stronę nosa od elektrody Fz)
- Montujemy także elektrody M1 i M2.
Analiza
- Filtrujemy sygnał w paśmie 0,5-20 Hz.
- Za pomocą ICA w SVAROGU (Analiza→ICA) rozkładamy sygnał na komponenty i usuwamy ten komponent, w którym obserwujemy aktywność elektryczną oka.
- Z ciągłego zapisu wycinamy fragmenty od −300 ms do +800 ms (zero oznacza moment wystąpienia bodźca). W czasie wycinania badamy wycinane fragmenty pod względem zakresu amplitudy (wszystkie kanały powinny mieć amplitudę w granicach ±75 μV).
- Rysujemy średni potencjał we wszystkich kanałach.
- Identyfikujemy załamki N1. Mierzymy ich amplitudę w stosunku do zera.
- Porównujemy amplitudy uzyskane w obu warunkach za pomocą odpowiedniego testu statystycznego (porównanie warunków ze skrajnymi wartościami amplitudy) — zastosuj test permutacyjny (opisany poniżej) lub test t-Studenta/nieparametryczny odpowiednik).
- liczymy różnicę ERP dla częstego i rzadkiego bodźca i umieszczamy wszystkie trzy krzywe na wykresie.
- Opis testu permutacyjnego
Pytanie: Czy częstość pokazywania bodźca wpływa na amplitudę potencjału N1? Jak stwierdzić czy amplitudy załamków N1 istotnie różnią się pomiędzy seriami?
Musimy przeprowadzić test statystyczny. Możemy skonstruować go np. tak: Mamy dwa warunki I i II. Jako statystykę przyjmiemy różnicę pomiędzy amplitudą zmierzoną w warunku II (AII) a amplitudą zmierzoną w warunku I (AI):
- S = AII − AI
Postawmy hipotezę zerową, że nie ma różnicy w amplitudzie pomiędzy warunkiem II a I oraz hipotezę alternatywną, że różnica taka występuje.
- H0: S = 0
- H1: S ≠ 0
Zgodnie z H0 dla wartości S nie ma różnicy czy realizacja została zarejestrowana w warunkach I czy II, zatem można losowo poprzypisywać numery warunków do realizacji i w ten sposób uzyskać rozkład statystyki S pod warunkiem prawdziwości H0, czyli obliczyć średnie potencjały dla „pomieszanych” tagów, wyliczyć średnie potencjały dla sztucznie wygenerowaych grup, i wyliczyć różnicę amplitud dla tych średnich, czyli wartość statystyki dla hipotezy H0.
Zaimplementuj test permutacyjny zgodny z powyższą koncepcją.
Eksperyment 2: rejestracja i analiza potencjału P3 - GOTOWE
Rejestracja
- Paradygmat:
- z odległości około 40 cm badany obserwuje średniej wielkości kwadrat; kwadraty występują w dwóch jasnych kolorach.
- Bodźce trwają 300 ms, poprzedzane punktem fiksacji wyświetlanym przez 0,5 s. Przerwa między próbami jest losowana i wynosi 0,6-1 s (punkt fiksacji też jest wyświetlany).
- Proporcja wystapień bodźców koloru pierwszego i drugiego wynosi 1:6. Zadbaj, aby bodźce rzadko występujące nie pojawiały się bezpośrednio po sobie.
- Zadaniem badanego jest zareagowanie naciśnięciem klawisza klawiatury na kwadrat w rzadkim kolorze (w instrukcji do badania podajemy jaki to kolor).
- informacja co do koloru wyświetlanego bodźca powinna być zapisaywana do tagów.
- Wykonujemy tyle realizacji aby zarejestrować 100 powtórzeń bodźców rzadkich.
- Pomiar:
- Zakładamy czepek i elektrody w systemie 10-20, dbamy o to by opory pomiędzy elektrodami były poniżej 5 kΩ i różnice pomiędzy oporami różnych elektrod nie przekraczały 20%.
- Elektrodę GND mocujemy w otworze czepka odpowiadającym pozycji AFz (na linii centralnej 10% w stronę nosa od elektrody Fz)
- Montujemy także elektrody M1 i M2, będziemy ich używać w montażu i w czasie analizy jako referencji typu połączone uszy.
- Częstość próbkowania 256 Hz.
Analiza
- Filtrujemy sygnał w paśmie 1-20 Hz w SVAROGU.
- Za pomocą ICA w SVAROGU (Analiza-> ICA) rozkładamy sygnał na komponenty i usuwamy ten komponent, w którym obserujemy aktywność elektryczną oka.
- Z ciągłego zapisu wycinamy fragmenty od −300 ms do +1000 ms (zero oznacza moment wystąpienia bodźca). W czasie wycinania badamy wycinane fragmenty pod względem zakresu amplitudy (wszystkie kanały powinny mieć amplitudę w granicach ±75 μV).
- Uśredniamy osobno realizacje dla każdego koloru kwadratu.
- Nakładamy na siebie na rysunkach oba typy średnich.
- Wyznaczamy amplitudę P3 i liczymy test statystyczny pomiędzy warunkami.
- dodatkowo z plików generowanych przez Psychopy (*.csv) wiciągamy informację dotyczącą szybkości i poprawności rekacji
- na odcinkach przed bodźcem w okolicach potylicznych i ciemieniowych liczymy widmo, aby oszacowac moc pasma alfa i beta.
- sprawdzamy hipotezę o zależności pomiędzy mocą alfy i bety oraz szybkości i poprawności reakcji.
Można też policzyć P300 w blokach po 25 wystapień i zobaczyć, czy jest jakas zależność pomiędzy amplitudą załamka a mocą w tych dwóch pasmach oraz wskaxnikacmi behawioralnymi.
MACKU - tutaj moga też pociczyć ROC i AUC
Zadanie 3. Analiza Heartbeat-Evoked Potential (HEP)
Celem tego zadania jest zaobserwowanie występowania ERP związanego z działaniem serca (szczegóły można doczytać tutaj: [1]. W zadaniu tym wykorzystany dane spoczynkowe zebrane podczas pierwszej rejestracji.
- w pierwszym kroku sygnał montujemy i filtrujemy;
- następnie zaznaczamy fragmenty sygnału, w których widzimy artefakty;
- w drugim robimy detekcję załamków R z EKG — po ich podstawie będziemy cieli sygnał (−200-600 ms po R);
- następnie uśredniamy otrzymane odcinki.