WnioskowanieStatystyczne/Zmienne losowe i generatory liczb pseudolosowych

Pojęcia wstępne

Zmienna losowa

Intuicyjnie

Zmienna losowa to taka zmienna, która przyjmuje pewną konkretną wartość w wyniku przeprowadzenia pomiaru lub eksperymentu. Na przykład zmienną losową jest liczba oczek, która wypada na kostce do gry. Dopóki trzymamy kostkę w ręce to nie wiemy jaką wartość ta zmienna przyjmie, konkretną wartość zmienna ta przyjmuje po rzucie. Jednak w kolejnych rzutach nie wiemy jakie będą jej wartości.

Bardziej formalnie

Zmienna losowa to funkcja przypisująca zdarzeniom elementarnym liczby.

Zupełnie formalnie

Do formalnej definicji potrzebne jest nam pojęcie przestrzeni probabilistycznej: Przestrzeń probabilistyczna to układ trzech elementów [math](\Omega, F,P)[/math], gdzie:

• [math]\Omega[/math] jest pewnym zbiorem, zwanym przestrzenią zdarzeń elementarnych,
• [math]F[/math] jest [math]\sigma[/math]-ciałem podzbiorów zbioru [math]\Omega[/math]. Elementy tego [math]\sigma[/math]-ciała nazywane są zdarzeniami losowymi,
• [math]P: F\rightarrow [0,1][/math] jest miarą probabilistyczną, tzn.
  • [math]P(A) \ge 0 [/math] dla każdego [math]A \in F[/math],
  • [math]P(\Omega) = 1[/math],
  • jeżeli zbiory [math]A_1, A_2,\dots,A_n \in F[/math] są parami rozłączne, to [math]P\left( \bigcup\limits_{i=1}^{\infty} A_i \right ) = \sum_{i=1}^{\infty} P(A_i) [/math].

Niech [math](\Omega, F,P)[/math] będzie przestrzenią probabilistyczną. Zmienną losową nazywamy dowolna funkcję [math]X[/math], określoną na przestrzeni zdarzeń elementarnych [math]\Omega[/math], o wartościach ze zbioru liczb rzeczywistych i mierzalną względem przestrzeni [math](\Omega, F,P)[/math]. Zmienna losowa jest ciągła jeśli jej zbiór wartości jest ciągły, lub dyskretna, jeśli jej zbiór wartości jest dyskretny.

Rozkład prawdopodobieństwa

Rozkład prawdopodobieństwa — (rozkład zmiennej losowej) miara probabilistyczna określona na [math]\sigma[/math]-ciele podzbiorów zbioru wartości zmiennej losowej, pozwalająca przypisywać prawdopodobieństwa zbiorom wartości tej zmiennej, odpowiadającym zdarzeniom losowym.

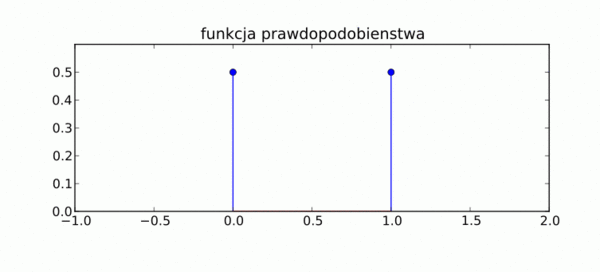
Dla zmiennej losowej dyskretnej możemy wprowadzić pojęcie funkcji prawdopodobieństwa: [math]P(X=x_i) = p_i[/math]

Przykład: Dla rzutów monetą funkcję prawdopodobieństwa można zobrazować jako tabelkę:

	Zdarzenie:	orzeł	reszka
zmienna losowa	[math]x_i[/math]	0	1
prawdopodobieństwo	[math]p_i[/math]	1/2	1/2

Można też przedstawić ją na wykresie:

Dla zmiennej losowej ciągłej zamiast funkcji prawdopodobieństwa wprowadzamy funkcję gęstości prawdopodobieństwa. Jest to funkcja określona na zbiorze liczb rzeczywistych posiadająca następujące własności:

• jest nieujemna: [math]f(x) \ge 0 [/math]
• prawdopodobieństwo tego, że zmienna losowa przyjmie wartość z przedziału [math](a,b][/math]: [math] \int_a^b f(x) dx = P(a\lt X \le b) [/math]

• Prawdopodobieństwo tego, że zmienna losowa przyjmie dowolną wartość: [math] \int_{-\infty}^{+\infty} f(x) dx = P(-\infty \lt X \le +\infty) = 1 [/math]

Dystrybuanta

Dystrybuantą zmiennej losowej [math]X[/math] nazywamy funkcję [math]F(x)[/math] określoną na zbiorze liczb rzeczywistych jako: [math]F(x) = P(X \le x)[/math]

czyli wartość dystrybuanty w punkcie [math]x[/math] jest prawdopodobieństwem, że zmienna losowa przyjmie wartość nie większą niż [math]x[/math].

• Dla zmiennej dyskretnej:

[math]F(x)=P(X \le x) = \sum_{x_i\lt x}{P(X = x_i) } = \sum_{x_i\lt x}p_i[/math]

• Dla zmiennej losowej ciągłej z funkcją gęstości prawdopodobieństwa [math]f[/math]:

[math]F(x) = P(X \le x)= \int_{-\infty}^x f(s) ds [/math]

Zauważmy ścisły związek dystrybuanty z funkcją prawdopodobieństwa w przypadku dyskretnym i funkcją gęstości prawdopodobieństwa w przypadku ciągłym.

Przykład z monetą:

Momenty

Dla zmiennej losowej można obliczyć momenty zwykłe lub centralne.

Moment zwykły

rzędu [math]k[/math] zmiennej losowej [math]X[/math] to wartość oczekiwana [math]k[/math]-tej potęgi tej zmiennej. Oblicza się go tak:

• dla dyskretnej zmiennej losowej

[math]m_k = E(X^k) = \sum_{i} {x_i^k p_i} [/math]

tu [math]p_i[/math] oznacza prawdopodobieństwo, że [math]X = x_i[/math]

• dla ciągłej zmiennej losowej

[math] m_k = E(X^k) = \int\limits_{-\infty}^{\infty} {x^k f(x)dx}[/math]

tu [math]f(x)[/math] jest funkcją gęstości prawdopodobieństwa.

Zauważmy, że pierwszy moment zwykły to średnia.

Moment centralny

rzędu [math]k[/math] zmiennej losowej [math]X[/math] to wartość oczekiwana [math]k[/math]-tej potęgi funkcji [math][x_i - E(x_i)][/math]. Zatem możemy go obliczyć tak:

• dla dyskretnej zmiennej losowej

[math] \mu_k = E\left( \left[ X-E(X) \right] ^k \right) = \sum_{i} {\left[x_i-E(X)\right]^k p_i} [/math]

• dla ciągłej zmiennej losowej

[math] \mu_k = E\left(\left[X-E(X)\right]^k\right) = \int\limits_{-\infty}^{\infty} { \left[X-E(X)\right]^k f(x)dx} [/math]

Uwaga:

• Drugi moment centralny ma swoją nazwę. Jest to wariancja, często oznaczana przez [math]\sigma^2[/math].
• Trzeci moment centralny przydaje się do badania symetrii rozkładu. Przyjmuje on wartość 0 dla zmiennych o rozkładzie symetrycznym, wartości ujemne dla zmiennych o rozkładzie wydłużonym w lewą stronę i wartości dodatnie dla zmiennych o rozkładzie wydłużonym w prawą stronę.
• Czwarty moment centralny jest przydatny do konstrukcji miary spłaszczenia rozkładu zmiennej losowej kurtozy. Definiuje się ją następująco:

[math] \mathrm{Kurt} = \frac{\mu_4}{\mu_2^4} - 3 [/math]

Rozkłady prawdopodobieństwa można podzielić ze względu na wartość kurtozy na rozkłady:

• mezokurtyczne — wartość kurtozy wynosi 0, spłaszczenie rozkładu jest podobne do spłaszczenia rozkładu normalnego (dla którego kurtoza wynosi dokładnie 0)
• leptokurtyczne — kurtoza jest dodatnia, wartości cechy bardziej skoncentrowane niż przy rozkładzie normalnym
• platokurtyczne — kurtoza jest ujemna, wartości cechy mniej skoncentrowane niż przy rozkładzie normalnym

Kwantyle

Kwantylem rzędu p, gdzie [math]0 \leqslant p \leqslant 1[/math], w rozkładzie empirycznym [math] P_{X} [/math] zmiennej losowej [math]X[/math] nazywamy każdą liczbę [math]x_{p}[/math], dla której spełnione są nierówności

[math] P_X((-\infty, x_p]) \geqslant p [/math]

oraz

[math] P_X([x_p,\infty)) \geqslant 1-p. [/math]

W szczególności, kwantylem rzędu p jest taka wartość [math]x_{p}[/math] zmiennej losowej, że wartości mniejsze lub równe od [math]x_{p}[/math] są przyjmowane z prawdopodobieństwem co najmniej p, zaś wartości większe lub równe od [math]x_{p}[/math] są przyjmowane z prawdopodobieństwem co najmniej 1−p.

Możemy zatem myśleć o obliczaniu kwantyla tak:

• zaobserwowaliśmy n wartości zmiennej losowej,
• zapiszemy te wartości na liście,
• następnie listę tę sortujemy w porządku rosnącym,
• kwantylem rzędu p jest albo element znajdujący się na liście w pozycji np jeśli np jest całkowite albo średnią z elementów położonych najbliżej np w przeciwnym wypadku.

Nazwy poszczególnych kwantyli

Kwantyl rzędu 1/2 to inaczej mediana (ściślej zależy to od definicji mediany, przy jej obliczaniu z próbki o parzystej liczbie elementów często stosuje się średnią arytmetyczną dwóch środkowych elementów, szczegóły są w artykule).
Kwantyle rzędu 1/4, 2/4, 3/4 są inaczej nazywane kwartylami.
Kwantyle rzędu 1/5, 2/5, 3/5, 4/5 to inaczej kwintyle.
Kwantyle rzędu 1/10, 2/10, ..., 9/10 to inaczej decyle.
Kwantyle rzędu 1/100, 2/100, ..., 99/100 to inaczej percentyle.

Pseudolosowość

W obliczeniach numerycznych często korzystamy z liczb „losowych”. Tak naprawdę sekwencje liczb, których używamy są jedynie pseudolosowe, tzn. są wytwarzane w deterministyczny (algorytmiczny) sposób, ale sekwencja generowanych wartości ma pewne cechy losowości. W idealnym przypadku cechą tą jest nieprzewidywalność: na podstawie obserwacji dotychczasowych wartości sekwencji niemożliwe jest podanie kolejnych wartości. W praktyce oznacza to nie możność ustalenie ziarna lub stanu wewnętrznego generatora na podstawie obserwacji dowolnie długiego ciągu wygenerowanych bitów. Stan generatora przechowywany jest na zmiennych o skończonej precyzji. Jeśli stan jest przechowywany na [math]n[/math] bitach to górną granicą na długość unikalnego ciągu liczb jest [math]2^n[/math]. Zazwyczaj unikalna sekwencja jest jednak krótsza. Wynika stąd, że generatory liczb pseudolosowych mają okres, po którym sekwencja liczb powtarza się. Podstawowe generatory liczb pseudolosowych wytwarzają liczby podlegające rozkładowi jednostajnemu (płaskiemu).

Istnieją generatory „prawdziwych” liczb losowych, które są osobnymi urządzeniami. Liczy przez nie dostarczane są pewnymi parametrami jakichś procesów fizycznych, przebiegających w tych urządzeniach (zależnie od producenta). Do naszych zastosowań w zupełności wystarczą liczby generowane przez algorytmy komputerowe.

Proste generatory liczb pseudolosowych można otrzymać jako funkcje używające operacji dzielenia modulo (generatory kongruencyjne):

[math]x_{n+1}=f(x_n,x_{n-1}, ..., x_{n-k})\mod M[/math].

Zakładamy, że argumentami funkcji [math]f[/math] są liczby całkowite ze zbioru [math]{0, 1, ...,M-1}[/math]. Dla ustalenia uwagi mogą to być generatory liniowe typu:

[math] x_{n+1}= (ax_{n} + c )\mod M[/math]

Przykład generatora liniowego

Dla przykładu zaimplementujmy jeden taki generator:

 
# -*- coding: utf-8 -*-

import numpy as np
import pylab as py
def gen(x,N=1):
    '''Przykład generatora liniowego. 
       funkcja zwraca liczby pseudolosowe z przedziału [0,1)
       x - ziarno, 
       N - ile liczb zwrócić'''
    m=8191
    a=101
    c=1731
    y=np.zeros(shape=(N,))
    for i in range(N):
        x=(a*x+c) % m
        y[i]= float(x)/m
    return y    
x=gen(23,100000)
py.hist(x)
py.show()

Liczby m, a, c są parametrami generatora. Liczba x, od której startuje generator nazywana jest ziarnem generatora (ang. seed). Funkcja py.hist() zlicza i wyrysowuje histogram (czy wiemy co to jest histogram?).

• Wywołaj funkcję gen dla tego samego ziarna kilka razy zaobserwuj powtarzalność wartości.

W module numpy mamy do dyspozycji generator liczb pseudolosowych oparty na algorytmie Mersenne Twister

# -*- coding: utf-8 -*-
"""
kod demonstrujacy pseudolosowosc
"""
import numpy as np
seed=3
np.random.seed(seed)
x=np.random.random(5)

np.random.seed(seed)
y=np.random.random(5)
print 'x: ',x
print 'y: ',y

• Zaobserwuj powtarzalność wartości.
• Wygeneruj i wykreśl 200 kolejnych liczb pseudolosowych.

# -*- coding: utf-8 -*-
import numpy as np
import pylab as py
seed=3
np.random.seed(seed)
x=np.random.random(200)

py.plot(x,'.')
py.show()

Testy jakości

Dla wyżej wymienionych generatorów, proszę wykonać następujące testy:

• zobrazować rozkład prawdopodobieństwa (narysować histogram);
• test korelacji na rysunku: sporządzić wykres gdzie na jednej osi są wartości [math]x_n[/math] na drugiej zaś wartości [math]x_{n+1}[/math].

# -*- coding: utf-8 -*-

import numpy as np
import pylab as py
def gen(x,N):
    m=8765132137 #8191
    a=42347#101
    c=1731
    y=np.zeros(shape=(N,))
    for i in range(N):
        x=(a*x+c) % m
        y[i]= float(x)/m
    return y


N=50000
x=gen(23,N)

py.subplot(2,1,1)
py.hist(x,30,normed = True)
py.subplot(2,1,2)
py.plot(x[:-1],x[1:],'.')
py.xlabel('x_n')
py.ylabel('x_{n+1}')
py.show()

Bardziej wyczerpujące baterie testów jakości generatorów można znaleźć na przykład w:

• http://csrc.nist.gov/groups/ST/toolkit/rng/index.html
• http://www.phy.duke.edu/~rgb/General/rand_rate.php

Zmienne losowe w module scipy.stats

Wstęp

Zmienne losowe w module scipy.stats są zaimplementowane jako dwie klasy: stats.rv_continuous (bazuje na niej ponad 80 typów rozkładów ciągłych zmiennych losowych) i stats.rv_discrete (bazuje na niej 10 typów rozkładów dyskretnych zmiennych losowych). Aktualną listę dostępnych rozkładów można uzyskać np. przy pomocy następującego skryptu:

from scipy import stats
dc= [d for d in dir(stats) if isinstance(getattr(stats,d), stats.rv_continuous)]
print dc

Przykładowo: zmienne losowe o rozkładzie normalnym są reprezentowane przez klasę norm.

Funkcje przydatne do pracy ze zmiennymi losowymi dostępne są jako metody

Obiekty reprezentujące zmienne losowe podlegające konkretnym rozkładom posiadają następujące metody:

• rvs: generator zmiennych losowych danego typu;
• cdf: dystrybuanta (ang. Cumulative Distribution Function);
• ppf: funkcja odwrotna do dystrybuanty (ang. Percent Point Function (Inverse of CDF));
• stats: zwraca momenty centralne rozkładu (średnią, wariancję, skośność i kurtozę);
• moment: zwraca niecentralne momenty rozkładu.
• pdf: funkcja gęstości prawdopodobieństwa (ang. Probability Density Function);
• pmf dla rozkładów dyskretnych pdf jest zamienione na funkcję prawdopodobieństwa (ang. probability mass function; masa przez analogię z gęstością masy i masą punktową);
• sf: funkcja przeżycia (ang. Survival Function) (1−CDF);
• isf: funkcja odwrotna do funkcji przetrwania (ang. Inverse Survival Function (Inverse of SF));

Dla przykładu zobaczmy działanie tych metod dla zmiennych losowych z rozkładu normalnego:

import scipy.stats as st
import pylab as py
import numpy as np

# generowanie 10000 liczb z rozkładu normalnego 
x = st.norm.rvs(size=10000)
py.subplot(2,2,4)
py.hist(x)
py.title('Histogram')
py.xlabel(u'wartość zmiennej')
py.ylabel(u'ilość zliczeń')

# wykreślenie gęstości prawdopodobieństwa
os_x = np.arange(-3,3,0.01)
y=st.norm.pdf(os_x)
py.subplot(2,2,3)
py.plot(os_x,y)
py.title(u'rozkład gęstości prawdopodobieństwa: pdf')
py.xlabel(u'wartość zmiennej')
py.ylabel(u'gęstość prawdopodobieństwa')

# wykreślenie dystrybuanty
z= st.norm.cdf(os_x)
py.subplot(2,2,1)
py.plot(os_x,z)
py.title(u'Dystrybuanta: cdf')

py.xlabel(u'wartość zmiennej')
py.ylabel(u'prawdopodobieństwo')

# wykreślenie funkcji odwrotnej do dystrybuanty
os_p = np.arange(0,1,0.01)
f=st.norm.ppf(os_p)
py.subplot(2,2,2)
py.plot(os_p,f)
py.title(u'funkcja odwrotna do dystrybuanty: ppf')
py.ylabel(u'wartość zmiennej')
py.xlabel(u'prawdopodobieństwo')
py.show()

Zmienne losowe mogą być używane na jeden z dwóch sposobów: można podawać wszystkie parametry opisujące rozkład w każdym wywołaniu metody, albo wytworzyć obiekt reprezentujący rozkład o konkretnych parametrach (w dokumentacji scipy jest to nazywane zamrażaniem parametrów rozkładu, ang. freezing) Jako przykład zobaczmy funkcję odwrotną do dystrybuanty rozkładu normalnego N(2, 9):

>>> import scipy.stats as st
>>> print st.norm.ppf(0.05, loc=2, scale=3)
-2.93456088085
>>> my_norm = st.norm(loc=2,scale=3)
>>> print my_norm.ppf(0.05)
-2.93456088085

Pomoc do poszczególnych dystrybucji

Pełną dokumnetację każdej dystrybucji mamy dostępną w postaci docstringów. Dla przykładu:

help(st.nct) .

wypisuje pełną informację z docstring o niecentralnym rozkładzie t. Podstawowe informacje można uzyskać wypisując treść pola extradoc

>>> print st.nct.extradoc 
Non-central Student T distribution
df**(df/2) * gamma(df+1)
nct.pdf(x,df,nc) = --------------------------------------------------
2**df*exp(nc**2/2)*(df+x**2)**(df/2) * gamma(df/2)
for df > 0, nc > 0.

Generowanie zmiennych losowych podlegającym różnym rozkładom prawdopodobieństwa

Podstawowe typy generatorów liczb losowych wytwarzają liczby losowe podlegające rozkładowi jednostajnemu. Zastanowimy sie teraz jak mając zmienne losowe z rozkładu jednostajnego wytworzyć zmienne losowe o innych rozkładach.

Rozkład dwumianowy

Zmienna losowa, która zlicza liczbę sukcesów [math]k[/math] w [math]n[/math] próbach, gdzie [math]p[/math] jest prawdopodobieństwem sukcesu w pojedynczej próbie, podlega rozkładowi dwumianowemu [więcej o rozkładzie dwumianowym]:

[math]P_n(k)=\left( \begin{array}{c} n \\ k \end{array} \right) p^kq^{n-k}=\frac{n!}{k!(n-k)!}p^kq^{n-k} [/math]

Jak z rozkładu jednostajnego wytworzyć zmienne losowe o rozkładzie dwumianowym?

• Wykonać symulację!

# -*- coding: utf-8 -*-
import numpy as np
import pylab as py


def gen_binom(n,p,N):
	'''funkcja zwracająca zmienną losową z rozkładu dwumianowego: 
	ilość sukcesów w n próbach przy prawdopodobieństwie sukcesu p
	parametry:
		n: ilość prób
		p: prawdopodobieństwo sukcesu
		N: ilość liczb do generowania	
	funkcja zwraca:
		N liczb będącymi ilościami sukcesów
	'''
	k = np.zeros(N)
	# w pętli wytwarzam pojedyncze zmienne losowe
	# losuję n liczb z rozkładu jednostajnego [0,1) i jako sukcesy
	#traktuję wylosowanie liczby nie większej niż p
	for i in range(N):
		r = np.random.random(size=n)
		k[i]=np.sum(r<=p)
	return k

# kod testujący
n=20
N=100000
p=0.8
x = gen_binom(n,p,N)
bins =range(21)
py.hist(x,bins)
py.show()

Zadanie

Z oszacowań agencji wynika, że średnio 2 z 3 reklam spotyka się z pozytywnym odzewem. Akcja marketingowa obejmuje 12 reklam. Niech [math]X[/math] oznacza liczbę reklam skutecznych. Czy [math]X[/math] podlega rozkładowi dwumianowemu? Jakie jest prawdopodobieństwo, że 10 reklam będzie skutecznych? Prawdopodobieństwo obliczyć ze wzoru oraz korzystając z symulacji.

Wskazówka informacje o zmiennych z rozkładu dwumianowego (binom) można uzyskać tak:

# >>> print st.binom.extradoc
#   Binomial distribution
#
#   Counts the number of successes in *n* independent
#   trials when the probability of success each time is *pr*.
#
#   binom.pmf(k,n,p) = choose(n,k)*p**k*(1-p)**(n-k)
#   for k in {0,1,...,n}

Odp: p = 0,127

♦

Zadanie

Na egzaminie testowym jest 30 pytań. Na każde pytanie są podane cztery możliwe odpowiedzi, z czego tylko jedna jest prawdziwa. Za prawidłową odpowiedź student otrzymuje 1 punkt a za fałszywą −0,5 punktu. Próg zaliczenia wynosi 15 punktów. Oblicz prawdopodobieństwo, że udzielając czysto losowych odpowiedzi student zaliczy egzamin.

♦

Rozkład Poissona

[math] P(x)=\frac{\mu^x e^{-\mu}}{x!} [/math] Rozkładowi Poissona podlegają zmienne losowe zliczające w jednostce czasu ilość zdarzeń o niskim prawdopodobieństwie zajścia. Np. ilość rozpadów promieniotwórczych na jednostkę czasu [więcej o rozkładzie Poissona]

Przykład

Lekarz pełniący dyżur w szpitalu jest wzywany do pacjentów średnio 3 razy w ciągu nocy. Załóżmy, że liczba wezwań na noc podlega rozkładowi Poissona. Jakie jest prawdopodobieństwo, że noc upłynie lekarzowi spokojnie? U nas [math]\mu=3[/math], [math]x=0[/math] więc

[math] P(0) = \frac{3^0e^{-3}}{0!} = e^{-3} = 0,0498 [/math]

Przykład

Jak ze zmiennych podlegających rozkładowi jednostajnemu uzyskać zmienne podlegające rozkładowi Poissona?

Wykonać symulację wynikającą z następujących spostrzeżeń:

• Weźmy jednostkę czasu. Ma w niej zachodzić średnio [math]\mu[/math] zdarzeń.
• Podzielmy jednostkę czasu na NT odcinków o jednakowej długości.
• Prawdopodobieństwo, że zdarzenie zajdzie w konkretnym odcinku jest [math]p=\frac{\mu}{NT}[/math] Takie prawdopodobieństwo ma też wylosowanie przy pomocy generatora liczb z rozkładu jednostajnego [0,1) liczby nie większej niż p.
• Zatem, aby wytworzyć jedną liczbę z rozkładu Poissona można policzyć ile spośród NT liczb z rozkładu jednostajnego [0,1) jest nie większych niż p.

# -*- coding: utf-8 -*-
import numpy as np
import pylab as py

def gen_poiss(mi,NT,N):
	'''funkcja zwracająca zmienne losowe z rozkładu poissona: 
	średnia ilość zdarzeń o niskim prawdopodobieństwie w jednostce czasu
	parametry:
		mi: średnia ilość zdarzeń
		NT: ilość odcinków czasu
		N: ilość liczb do generowania	
	funkcja zwraca:
		N liczb będących zliczeniami zdarzeń
	'''
	p = float(mi)/NT
	k = np.zeros(N)
	# w pętli wytwarzam pojedyncze zmienne losowe
	# losuję NT liczb z rozkładu jednostajnego [0,1) i jako zajście zdarzenia
	# traktuję wylosowanie liczby nie większej niż p. Ilość zdarzeń to liczba z rozkładu Poissona
	for i in range(N):
		r = np.random.random(size=NT)
		k[i]=np.sum(r<=p)
	return k
	
# kod testujący
mi=4
N=10000
NT = 10000
x = gen_poiss(mi,NT,N)
bins =range(31)
py.hist(x,bins)
py.show()

Rozkład normalny i Centralne Twierdzenie Graniczne

Gęstość prawdopodobieństwa rozkładu normalnego dana jest wzorem:

[math]f(x)=\frac{1}{\sqrt{2 \pi \sigma}} e^{ -\frac{(x-\mu)^2}{2 \sigma^2}}[/math] gdzie: [math]\mu[/math] — średnia, [math]\sigma[/math] — odchylenie standardowe ([math]\sigma^2[/math] — wariancja).

Jeden ze sposóbw wytwarzania zmiennych losowych o rozkładzie normalnym polega na zastosowaniu Centralnego Twierdzenia Granicznego.

[math]X=\frac{\sqrt{12}}{\sqrt{N}}\left(\sum_{n=1}^N Y_n -\frac{N}{2}\right)[/math]

gdzie [math]Y[/math] zmienna losowa z rozkładu jednostajnego [math][0,1)[/math] W granicy dużych [math]N[/math] rozkład zmiennej [math]X[/math] dąży do rozkładu normalnego [math]N(0,1)[/math].

Zadanie

Proszę:

• napisać funkcję gen_1(N), która zwraca liczbę losową X otrzymaną zgodnie powyższym wzorem przez sumowanie N liczb z rozkładu jednostajnego.
• napisać funkcję gen_CTG(N, N_liczb) korzystającą z gen_CTG_1(N) i zwracającą zadaną ilość liczb N_liczb
• narysować histogramy 10 000 liczb [math]X[/math] uzyskanych kolejno dla [math]N={1,2,...,12}[/math]
• Jakie parametry charakteryzują rozkład do którego zbiegają sumy? Przy każdym z powyższych histogramów wypisz średnią i wariancję z próby (funkcje np.mean i np.var).

♦

Problem: transformacja rozkładu normalnego

Rozkład o średniej 0 i wariancji 1 (notacja [math]N(0,1)[/math]) jest nazywany rozkładem standardowym i często jest oznaczany literą [math]Z[/math]. Dokonując odpowiedniej transformacji można z rozkładu [math]Z[/math] uzyskać dowolny inny rozkład normalny.

Proszę:

• wygenerować 100000 zmiennych losowych z rozkładu [math]N(0,1)[/math] (skorzystać z funkcji st.norm.rvs(loc=0, scale=1, size=100000))
• przetransformować je do zmiennych losowych [math]N(2,9)[/math].
• narysować histogramy zmiennych przed i po transformacji.

♦

Transformacja Boxa-Mullera

to inna popularna metoda metoda generowania liczb losowych o rozkładzie normalnym, na podstawie dwóch wartości zmiennej o rozkładzie jednostajnym na przedziale (0,1] http://en.wikipedia.org/wiki/Box-Muller_transform, ale nie będziemy się nią tu szerzej zajmować.

Przykład

Producent silników twierdzi, że jego silniki mają średnią moc 220 KM, a odchylenie standardowe wynosi 15 KM. Potencjalny klient testuje 100 silników. Jakie jest prawdopodobieństwo, że średnia z próby będzie mniejsza niż 217 KM?

Przypomnijmy, że z CTG dla dużych liczebności próby [math]n[/math] [math]\bar x \sim N(\mu,\sigma^2/n)[/math] (dowód). Zatem szukamy

[math]P(\bar x \lt 217) =P\left( Z\lt \frac{217-\mu}{\frac{\sigma}{ \sqrt{n}}} \right) = P\left( Z\lt \frac{217-220}{\frac{15}{ \sqrt{100}}} \right)=P(Z\lt -2)=0,0228[/math]

import scipy.stats as st
import pylab as py
import numpy as np

# ze wzoru
p=st.norm.cdf(-2)
print 'prawdopodobieństwo odczytane z dystrybuanty rozkładu normalnego: %(0).4f' %{'0':p}

# symulacja

mu=220
sig=15
N_prob=100

m_kryt=217

N_rep=int(1e4)
srednia=np.zeros(N_rep)
for i in range(N_rep):
    seria=st.norm.rvs(loc=mu, scale=sig, size=100)
    srednia[i]=np.mean(seria)

h=py.hist(srednia,30);

py.plot([m_kryt, m_kryt],[0, max(h[0])],'r')
p1=float(np.sum(srednia<=m_kryt))/N_rep
print 'prawdopodobieństwo uzyskane z symulacji: %(0).4f' %{'0':p1}
py.show()

Zadanie

Teraz kilka najprostszych zadań dotyczących rozkładu normalnego:

• Znajdźmy prawdopodobieństwo, że Z < −2,47. Proszę zrobić to na dwa sposoby: raz z użyciem wygenerowanych zmiennych z rozkładu normalnego, drugi raz z użyciem dystrybuanty norm.cdf

[odp: p = 0,0068]

♦

• Znaleźć prawdopodobieństwo P(|Z| < 2) [Odp: p = 0,9545]

♦

• Koncentracja zanieczyszczeń w półprzewodniku używanym do produkcji procesorów podlega rozkładowi normalnemu o średniej 127 cząsteczek na milion i odchyleniu standardowemu 22. Półprzewodnik może zostać użyty jedynie gdy koncentracja zanieczyszczeń spada poniżej 150 cząstek na milion. Jaka proporcja półprzewodników nadaje się do użycia?

Prawdopodobieństwo obliczyć korzystając z dystrybuanty rozkładu normalnego oraz z symulacji. [Opd: p = 0,852]

♦

Rozkład t

Gdy nie znamy odchylenia standardowego populacji [math]\sigma^2[/math] używamy w jego miejsce estymatora wariancji próby [math]s^2[/math] danego wzorem:

[math]s^2 =\frac{\sum(\bar x - x_i)^2}{n-1} [/math] gdzie n — rozmiar próby

Wtedy rozkład [math]Y=\frac{\bar X -\mu}{\frac{s}{\sqrt{n}}}[/math] nie podlega rozkładowi normalnemu. Jeśli populacja [math]X[/math] podlega rozkładowi normalnemu to [math]Y[/math] podlega rozkładowi t z n−1 stopniami swobody.

Zobaczmy na symulacji co to zmienia. Proszę obejrzeć wyniki dla kilku wartości N

# -*- coding: utf-8 -*-
import numpy as np
import pylab as py

N=3
N_liczb=10000
y_idealne=np.zeros(N_liczb)
m_idealne=np.zeros(N_liczb)
s_idealne=np.zeros(N_liczb)
y_est=np.zeros(N_liczb)
m_est=np.zeros(N_liczb)
s_est=np.zeros(N_liczb)
for i in range(N_liczb):
    x=np.random.randn(N)+2
    m_idealne[i]=np.mean(x)
    s_idealne[i]=1/np.sqrt(N)
    y_idealne[i]=(m_idealne[i]-2)/(s_idealne[i])
    s_est[i]=np.std(x)/np.sqrt(N)
    y_est[i]=(m_idealne[i]-2)/(s_est[i])

py.subplot(311)
py.plot(m_idealne)
py.title(u'średnia')
py.subplot(323)
py.plot(s_idealne)
py.title('odchylenie standardowe idealne')
py.subplot(324)
py.plot(s_est)
py.title('odchylenie standardowe estymowane')
py.subplot(325)
py.hist(y_idealne,30,(-4,4))
py.title(u'rozkład ilorazu dla wersji idealnej')
py.subplot(326)
py.hist(y_est,30,(-4,4))
py.title(u'rozkład ilorazu dla wersji estymowanej')


py.show()

Inne rozkłady uzyskiwane przez transformacje

Metoda odwracania dystrybuanty

Niech [math]\xi[/math] będzie zmienną losową o rozkładzie jednostajnym na przedziale [math](0,1][/math]. Jej dystrybuanta [math]J[/math] dana jest więc worem:

[math] J(x) = P(\xi \le x) = \left\{ \begin{array}{lrl} 0 & \mathrm{dla} & x\lt 0\\ x & \mathrm{dla} & 0 \le x \lt 1 \\ 1 & \mathrm{dla} & 1 \le x \end{array} \right. [/math]

oraz niech [math]F[/math] będzie dystrybuantą interesującego nas rozkładu. Jeśli [math]F[/math] jest funkcją odwracalną to zmienna losowa zdefiniowana jako:

[math]\eta = F^{-1}(\xi) [/math]

jest zmienną losową podlegającą rozkładowi o dystrybuancie [math] F[/math]. Własność tę łatwo sprawdzić. Ponieważ dla każdego [math]x \in R [/math] mamy:

[math] P(\eta \le x) = P(F^{-1} (\xi) \le x) = P(\xi \le F(x)) = F(x) [/math] więc [math]F[/math] jest dystrybuantą zmiennej losowej [math]\eta[/math].

Czyli jeśli znamy dystrybuantę interesującego nas rozkładu prawdopodobieństwa i dystrybuanta ta jest odwracalna, to możemy generować liczby z rozkładu o dystrybuancie [math]F[/math].

Przykład

Wygenerować liczby pseudolosowe z rozkładu wykładniczego o dystrybuancie:

[math]F(X) = 1-e^{-\lambda x} [/math]

Rozwiązanie:

• Znajdujemy funkcję odwrotną do dystrybuanty:

[math]G(u)=F^{-1}(u) = -\frac{1}{\lambda}\ln(1-u) [/math]

• Generujemy liczby losowe [math]u[/math] z przedziału [math](0,1][/math] i stosujemy transformację [math]G(u)[/math]
• Test generowanego rozkładu robimy przez porównanie dystrybuanty teoretycznej i empirycznej. Proszę zwrócić uwagę na funkcję estymującą dystrybuantę empiryczną

import pylab as py
import numpy as np


def gen_wykladniczy(lam, N):
	'''funkcja zwraca N liczb z rozkładu wykładniczego o parametrze lam
	korzystając z metody odwracania dystrybuanty
	Dystrybuanta rozkładu wykładniczego: F(x) = 1- exp(-lam*x)
	Funkcja do niej odwrotna: G(u) = -1/lam ln(1-u)'''

	u = np.random.random(N)
	return -1.0/lam* np.log(1.-u)
	
def dystrybuanta(X,od=0, do=4, krok=0.05):
	'''funkcja zwraca dystrybuantę empiryczną 
	zmiennej X na przedziale (od, do) z krokiem krok'''
	
	os_x = np.arange(od,do,krok)
	nx = len(os_x)
	N_liczb = len(X)
	D=np.zeros(nx) #wyzerowany wektor na naszą dystrybuantę
	for i in xrange(nx):
		D[i] = float(sum(X <= os_x[i]))/N_liczb
	return (os_x, D)
	
# testujemy: narysujemy dystrybuantę oczekiwaną i empiryczną
lam=3
N=10000

x = np.arange(0,4,0.01)
F = 1-np.exp(-lam*x)
X = gen_wykladniczy(lam, N)
(os_x, F_emp) = dystrybuanta(X,od=0, do=4, krok=0.1)
py.plot(x,F,'r',label = 'dystrybuanta teoretyczna')
py.plot(os_x, F_emp,'.b', label = 'dystrybuanta empiryczna')
py.legend( )
py.show()

Zauważmy, że nie zawsze jest łatwo wyznaczyć efektywnie [math]F^{-1}[/math] — jest tak na przykład w przypadku rozkładu normalnego. W takich sytuacjach można szukać przybliżonej wartości [math]F^{-1}[/math], rozwiązując numerycznie równanie: [math]F(x)=u[/math], co sprowadza się do znalezienia miejsc zerowych funkcji [math]H(x)=F(x)-u[/math].