Aliasing: Różnice pomiędzy wersjami
| Linia 5: | Linia 5: | ||
[[Plik:aliasingklatka.png]] | [[Plik:aliasingklatka.png]] | ||
| − | Przypomnijmy [[Przekształcenie Fouriera#label-eq:21|wzór na odwrotną transformację Fouriera]] sygnału ciągłego | + | Przypomnijmy [[Przekształcenie Fouriera#label-eq:21|wzór na odwrotną transformację Fouriera]] sygnału ciągłego |
| − | |||
<math> | <math> | ||
s(t)=\int_{-\infty}^{\infty}\hat{s}(f)e^{-i 2\pi t f} d f | s(t)=\int_{-\infty}^{\infty}\hat{s}(f)e^{-i 2\pi t f} d f | ||
| Linia 35: | Linia 34: | ||
z funkcji będącej (nieskończoną) sumą powtórzeń [[Przekształcenie Fouriera|transformaty Fouriera]] | z funkcji będącej (nieskończoną) sumą powtórzeń [[Przekształcenie Fouriera|transformaty Fouriera]] | ||
sygnału ciągłego, przesuwanej o wielokrotności odwrotności | sygnału ciągłego, przesuwanej o wielokrotności odwrotności | ||
| − | <math>\Delta t</math>. | + | <math>\Delta t</math>. |
| + | |||
| + | Innym sposobem pokazania tego efektu jest przedstawienie sekwencji dyskretnej <math>s[n]</math> jako iloczynu sygnału ciągłego <math>s(t)</math> z grzebieniem Diraca | ||
| + | |||
| + | <math> | ||
| + | D(t) = \sum_{k=-\infty}^{\infty} \delta(t-k\delta t) | ||
| + | </math> | ||
| + | |||
| + | Zgodnie z twierdzeniem o splocie, iloczyn w przestrzeni czasu będzie odpowiadał splotowi w dziedzinie częstości, czyli w dziedzinie częstości otrzymamy splot transformaty Fouriers sygnału <math>\hat{s}(t)</math> z transformatą Fouriera grzebienia Diraca <math>\hat{D}(t)</math>, którą poniżej wyliczymy: | ||
| + | |||
| + | <math> | ||
| + | \hat{D}(f) = \mathcal{F}(D(t)) = \mathcal{F}\left(\sum_{k=-\infty}^{\infty} \delta(t-k\Delta t) \right) = | ||
| + | \int_{-\infty}^{\infty} \sum_{k=-\infty}^{\infty} \delta(t-k\Delta t) e^{i 2\pi f t} dt | ||
| + | = | ||
| + | </math> | ||
| + | <math> | ||
| + | \sum_{k=-\infty}^{\infty} \int_{-\infty}^{\infty} \delta(t-k\Delta t) e^{i 2\pi f t} dt = | ||
| + | \sum_{k=-\infty}^{\infty} e^{i 2\pi f k\Delta t} dt | ||
| + | </math> | ||
| + | |||
| + | Otrzymaliśmy ogólny wynik -- transformata Fouriera grzebienia Diraca to również grzebień Diraca (w przestrzeni częstości). | ||
| + | |||
| + | Przypomnijmy (np. z [[Systemy_liniowe_niezmiennicze_w_czasie_(LTI)|rozważań o systemach liniowych niezmienniczych w czasie]]), że splot z deltą Diraca w zerze jest identycznością, a splot z <math>\delta(t-kT)</math> przesuwa funkcję o <math>kT</math>. Z liniowości splotu dostajemy -- jak pozyżej -- sumę powtórzeń [[Przekształcenie Fouriera|transformaty Fouriera]] | ||
| + | sygnału ciągłego, przesuwanej o wielokrotności odwrotności | ||
| + | <math>\Delta t</math>. | ||
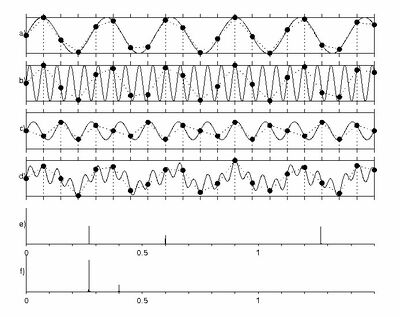
[[Plik:klasyczna_rys_5.jpg|thumb|center|400px|<figure id="fig:36"></figure>Próbkowanie (<math>\Delta t = 1</math>) sygnałów o częstościach: (a) 0.27, (b) 1.27 i (c) 0.6. | [[Plik:klasyczna_rys_5.jpg|thumb|center|400px|<figure id="fig:36"></figure>Próbkowanie (<math>\Delta t = 1</math>) sygnałów o częstościach: (a) 0.27, (b) 1.27 i (c) 0.6. | ||
| Linia 47: | Linia 70: | ||
wzrasta dwukrotnie w stosunku do mniejszego piku częstości 0.6, który "zawija się" z kolei na 0.4 | wzrasta dwukrotnie w stosunku do mniejszego piku częstości 0.6, który "zawija się" z kolei na 0.4 | ||
(w tym przypadku <math>r = 1</math> a "zawija się" dokładnie częstość <math>-0.6</math>)]] | (w tym przypadku <math>r = 1</math> a "zawija się" dokładnie częstość <math>-0.6</math>)]] | ||
| + | |||
| + | |||
| + | |||
<references/> | <references/> | ||
Wersja z 12:13, 25 paź 2015
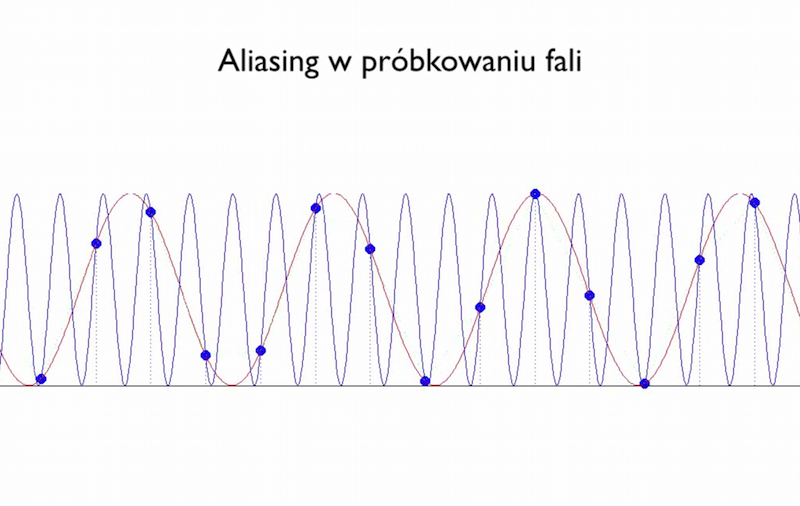
AS/ Przekształcenie Fouriera sygnałów dyskretnych, aliasing
Kliknij na tym napisie aby obejrzeć animację pokazującą efekt aliasingu na sygnale jednowymiarowym
Przypomnijmy wzór na odwrotną transformację Fouriera sygnału ciągłego [math] s(t)=\int_{-\infty}^{\infty}\hat{s}(f)e^{-i 2\pi t f} d f [/math]
Dyskretne wartości tego sygnału, próbkowane w chwilach [math]n \Delta t[/math], możemy odtworzyć z powyższgo równania dla [math]t = n \Delta t[/math]
[math] \sum_{r=-\infty}^\infty \int_\frac{(2r - 1)}{2\Delta t}^\frac{(2r + 1) }{2\Delta t} \hat{s}(f)e^{-i 2\pi n \Delta t f} d f \;\; \stackrel{f \rightarrow f+\frac{r}{\Delta t}}{=} \;\; [/math] [math] \sum_{r=-\infty}^\infty \int_\frac{-1}{2\Delta t}^\frac{1}{2\Delta t} \hat{s}\left(f + \frac{r}{\Delta t}\right)e^{-i 2\pi n \Delta t (f + \frac{r}{\Delta t})} d f [/math]
[math] = \int_\frac{-1}{2\Delta t}^\frac{1}{2\Delta t} \sum_{r=-\infty}^\infty \hat{s}\left(f + \frac{r}{\Delta t}\right)e^{-i 2\pi n \Delta t f} d f [/math]Szukając wartości sygnału w dyskretnych chwilach czasu, dostaliśmy w miejsce odwrotnej transformaty Fouriera całkę w ograniczonym zakresie z funkcji będącej (nieskończoną) sumą powtórzeń transformaty Fouriera sygnału ciągłego, przesuwanej o wielokrotności odwrotności [math]\Delta t[/math].
Innym sposobem pokazania tego efektu jest przedstawienie sekwencji dyskretnej [math]s[n][/math] jako iloczynu sygnału ciągłego [math]s(t)[/math] z grzebieniem Diraca
[math] D(t) = \sum_{k=-\infty}^{\infty} \delta(t-k\delta t) [/math]
Zgodnie z twierdzeniem o splocie, iloczyn w przestrzeni czasu będzie odpowiadał splotowi w dziedzinie częstości, czyli w dziedzinie częstości otrzymamy splot transformaty Fouriers sygnału [math]\hat{s}(t)[/math] z transformatą Fouriera grzebienia Diraca [math]\hat{D}(t)[/math], którą poniżej wyliczymy:
[math] \hat{D}(f) = \mathcal{F}(D(t)) = \mathcal{F}\left(\sum_{k=-\infty}^{\infty} \delta(t-k\Delta t) \right) = \int_{-\infty}^{\infty} \sum_{k=-\infty}^{\infty} \delta(t-k\Delta t) e^{i 2\pi f t} dt = [/math] [math] \sum_{k=-\infty}^{\infty} \int_{-\infty}^{\infty} \delta(t-k\Delta t) e^{i 2\pi f t} dt = \sum_{k=-\infty}^{\infty} e^{i 2\pi f k\Delta t} dt [/math]
Otrzymaliśmy ogólny wynik -- transformata Fouriera grzebienia Diraca to również grzebień Diraca (w przestrzeni częstości).
Przypomnijmy (np. z rozważań o systemach liniowych niezmienniczych w czasie), że splot z deltą Diraca w zerze jest identycznością, a splot z [math]\delta(t-kT)[/math] przesuwa funkcję o [math]kT[/math]. Z liniowości splotu dostajemy -- jak pozyżej -- sumę powtórzeń transformaty Fouriera sygnału ciągłego, przesuwanej o wielokrotności odwrotności [math]\Delta t[/math].