Ćwiczenia 1.1

Sygnał jako wekotr

Jak to rozumieć?

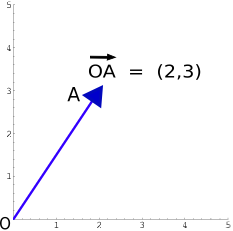
W najprostszej wersji znanej ze szkoły wektory rozumiane są tak jak na tym rysunku:

Koncepcje wektora można uogólnić i rozumieć go jako uporządkowany ciąg liczb, czyli współrzędnych wektora:

Łatwo sobie wyobrazić, że tą koncepcję można uogólnić na dowolną liczbę współrzędnych (wymiarów). Wtedy trudniej jest przedstawić go w postaci strzałki, ale możemy przedstawić go np. tak, że kolejne współrzędne rysyjemy jako punkty na dwuwymiarowej płaszczyźnie (nr współrzędnej, wartość współrzędnej):

import pylab as py
import numpy as np

A = np.array([2,3])
py.subplot(2,1,1)
py.plot(A,'o')
py.xlim([-0.1, 1.1])
py.ylim([0,3.1])
py.ylabel('Wartość')

py.subplot(2,1,2)
py.stem(A)
py.xlim([-0.1, 1.1])
py.ylim([0,3.1])
py.ylabel('Wartość')
py.xlabel('Nr. próbki')
py.show()

Widać, że taka reprezentacja świetnie nadaje się do przedstawiania sygnałów dyskretnych (Sygnały ciągłe można rozumieć jako wektory w nieskończenie wymiarowej przestrzeni).