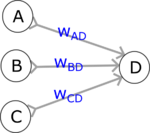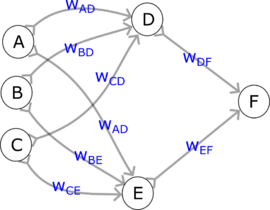TI/Sztuczne sieci neuronowe: Różnice pomiędzy wersjami
| Linia 43: | Linia 43: | ||
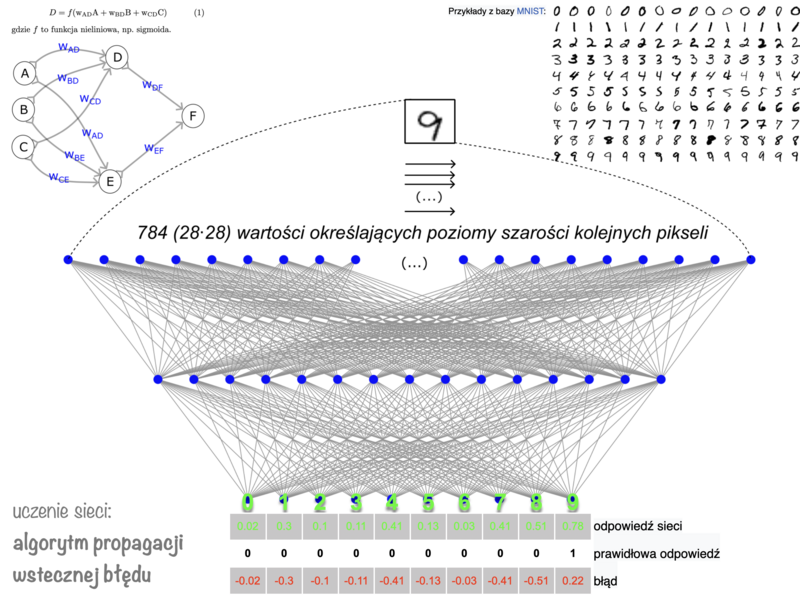
Powyższy rysunek ilustruje przykładową, prostą sieć z jedną warstwą ukrytą, w której poziomy szarości podawane są do kolejnych neuronów wartwy wejściowej. | Powyższy rysunek ilustruje przykładową, prostą sieć z jedną warstwą ukrytą, w której poziomy szarości podawane są do kolejnych neuronów wartwy wejściowej. | ||
* Według aktualnej wiedzy znacznie efektywniejszą architekturą są sieci splotowe (ang. [https://en.wikipedia.org/wiki/Convolutional_neural_network convolutional neural networks]), w których struktura wejścia odpowiada topologicznemu sąsiedztwu pikseli w dwóch wymiarach. | * Według aktualnej wiedzy znacznie efektywniejszą architekturą są sieci splotowe (ang. [https://en.wikipedia.org/wiki/Convolutional_neural_network convolutional neural networks]), w których struktura wejścia odpowiada topologicznemu sąsiedztwu pikseli w dwóch wymiarach. | ||
| − | * Współczene sieci mają zwykle znacznie więcej warstw ukrytych. | + | * Współczene sieci mają zwykle znacznie więcej warstw ukrytych — wtedy mówimy o [https://pl.wikipedia.org/wiki/Uczenie_g%C5%82%C4%99bokie głębokich sieciach neuronowych] (ang. ''deep neural networks''). |
Wersja z 18:08, 24 lip 2024
Spis treści
⬆ Neurony i wagi połączeń
Sztuczne sieci neuronowe konstruowane są z jednostek zwanych sztucznymi neuronami. Możemy o nich myśleć jako o komórkach pamięci komputera, przechowujących konkretne liczby (zmienne). Wartość zapisana w jednej takiej komórce ([math]\textsf{D}[/math]) jest w każdym kroku obliczana według stałego schematu:
- liczby z komórek (sztucznych neuronów) poprzedniej warstwy [math]\textsf{A B C}[/math] są mnożone przed odpowiednie wagi i dodawane do siebie: [math]\textsf{A} \textsf{w}_\textsf{AD} + \textsf{B} \textsf{w}_\textsf{BD} + \textsf{C} \textsf{w}_\textsf{CD}[/math]
- wyliczona powyżej suma ważona jest poddawana działaniu funkcji aktywacji [math]f[/math]: [math]\textsf{D} = f\left(\textsf{A} \textsf{w}_\textsf{AD} + \textsf{B} \textsf{w}_\textsf{BD} + \textsf{C} \textsf{w}_\textsf{CD}\right)[/math]
Obliczenia wykonywane przez przykładową sieć:
- W jednostkach po lewej ([math]\textsf{A B C}[/math]) znajdują się wartości (liczby), które dla uproszczenia oznaczymy również literami [math]\textsf{A B C}[/math]. Mogą one reprezentować wejście sieci (wtedy będzie to warstwa wejściowa) lub być wynikiem obliczeń poprzednich warstw sieci (wtedy będzie to warstwa ukryta).
- Wartości w neuronach [math]\textsf{D}[/math] i [math]\textsf{E}[/math] wyliczamy według podanego powyżej wzoru:
- [math]\textsf{D} = f\left(\textsf{A} \textsf{w}_\textsf{AD} + \textsf{B} \textsf{w}_\textsf{BD} + \textsf{C} \textsf{w}_\textsf{CD}\right)[/math]
- [math]\textsf{E} = f\left(\textsf{A} \textsf{w}_\textsf{AE} + \textsf{B} \textsf{w}_\textsf{BE} + \textsf{C} \textsf{w}_\textsf{CE}\right)[/math]
- W następnym kroku wyliczamy wartość dla neuronu ostatniej warstwy F:
- [math]\textsf{F} = f\left(\textsf{D} \textsf{w}_\textsf{DF} + \textsf{E} \textsf{w}_\textsf{EF}\right)[/math]
Wyliczoną w ten sposób wartość [math]\textsf{F}[/math] możemy uznać za "odpowiedź" tej sieci na podane na wejściu liczby [math]\textsf{A}[/math], [math]\textsf{B}[/math] i [math]\textsf{C}[/math].
Sztuczna sieć neuronowa sieć jest jednoznacznie określona przez strukturę połączeń oraz konkretne wartości wag [math]\textsf{w}_\textsf{XY}[/math], zwanych też parametrami sieci lub modelu; w roku 2024 liczby parametrów dużych modeli sięgają setek miliardów.
Przykład: rozpoznawanie cyfr za pomocą prostej sieci
Strukturę sieci dopasowujemy do wymiarów problemu.
Warstwa wejściowa
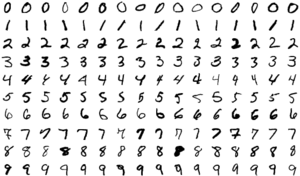
przyjmuje dane; jeśli sieć ma rozpoznawać obrazy w odcieniach szarości, na wejściu podamy liczby odpowiadające zaczernieniu kolejnych pikseli — dla obrazów o wymiarach 28*28 pikseli będzie ich 784.
Warstwa wyjściowa
— jej rozmiar zależy od formy oczekiwanych "odpowiedzi". Jeśli mają to być odpowiedzi tak/nie (np. na obrazku znajduje się szukany obiekt lub nie), wystarczyć może nawet jeden sztuczny neuron wyjściowy: jeśli zwracana wartość będzie mniejsza od jakiegoś progu, przyjmiemy "tak", w przeciwnym przypadku — "nie".
Jeśli sieć ma rozpoznawać znajdujące się na obrazach liczby, najwygodniej przypisać każdej liczbie jeden neuron wartwy wyjściowej. Wtedy idealną odpowiedzią sieci na liczbę 9 będzie wartość 1 w ostatnim neuronie, i zera w pozostałych. Takie wzorcowe odpowiedzi pojawiają się tylko w procesie uczenia sieci (jako oznaczenia zbioru uczącego), w praktycznym działaniu takiej sieci jako odpowiedź wybieramy neuron, w którym występuje najwyższa wartość.
Powyższy rysunek ilustruje przykładową, prostą sieć z jedną warstwą ukrytą, w której poziomy szarości podawane są do kolejnych neuronów wartwy wejściowej.
- Według aktualnej wiedzy znacznie efektywniejszą architekturą są sieci splotowe (ang. convolutional neural networks), w których struktura wejścia odpowiada topologicznemu sąsiedztwu pikseli w dwóch wymiarach.
- Współczene sieci mają zwykle znacznie więcej warstw ukrytych — wtedy mówimy o głębokich sieciach neuronowych (ang. deep neural networks).