Pracownia EEG/EEG spoczynkowe: Różnice pomiędzy wersjami
SuperAdmin (dyskusja | edycje) |
SuperAdmin (dyskusja | edycje) |
||
| Linia 907: | Linia 907: | ||
Wywołanie przykładowe: | Wywołanie przykładowe: | ||
| − | <source lang = | + | <source lang = python> |
t= np.arange(0,1,0.1) | t= np.arange(0,1,0.1) | ||
x = np.sin(2*np.pi*2*t) | x = np.sin(2*np.pi*2*t) | ||
| Linia 923: | Linia 923: | ||
Natomiast wywołanie: | Natomiast wywołanie: | ||
| − | <source lang =' | + | <source lang ='python'> |
t= np.arange(0,1,0.1) | t= np.arange(0,1,0.1) | ||
x = np.sin(2*np.pi*2*t) | x = np.sin(2*np.pi*2*t) | ||
Wersja z 19:50, 23 maj 2015
Podstawowe grafoelementy zapisu EEG i ich główne cechy
Rytm [math]\delta [/math]
Przebieg rytmu delta zaprezentowano na rysunku 1. Jest to wysokoamplitudowa aktywność o niskiej częstości (0-4 Hz) i czasie trwania co najmniej 1/4 s. Do celów praktycznych przyjęto, że dolną granicą częstości jest 0,5 Hz. Pojawiające się podczas głębokiego snu fale delta o amplitudzie przekraczającej 75 [math]\mu[/math]V nazywa się falami wolnymi (ang. slow wave activity, SWA). Występowanie SWA spowodowane jest wysoką synchronizacją neuronów kory (większą synchronizację spotyka się tylko podczas ataku epilepsji). Fale delta rejestruje się także podczas głębokiej medytacji, u małych dzieci i w przypadku pewnego rodzaju uszkodzeń mózgu.
Rytm [math]\theta [/math]
Rytmem teta (and. theta) (rys. 10) nazywamy aktywność w paśmie częstości od 3 do 7 Hz i rozpiętości (ang. peak-to-peak) rzędu kilkudziesięciu μV. Charakterystyczne fale teta występują np. w okresie snu płytkiego — przypuszcza się że w tym czasie następuje przyswajanie i utrwalanie uczonych treści. Fale teta są najczęściej występującymi falami mózgowymi podczas medytacji, transu, hipnozy, intensywnego marzenia, intensywnych emocji. Odmienny rodzaj fal teta jest związany z aktywnością poznawczą, kojarzeniem (w szczególności uwagą), a także procesami pamięciowymi (tzw. rytm FMΘ — frontal midline theta). Jest on obserwowany głównie w przyśrodkowej części przedniej części mózgu.
Cechy charakterystyczne:
- Rytmiczny przebieg o częstości 3-7 Hz.
- Najwyższa amplituda w stanie czuwania w okolicach linii środkowej i obszarach skroniowych.
- Rozkład amplitudy symetryczny na półkulach określonych przez płaszczyznę strzałkową
Cechy patologiczne:
- Asymetryczny rozkład amplitudy (dominacja rytmu na jednej półkuli) bądź też jego występowanie w zapisie tylko na jednym odprowadzeniu może świadczyć o patologii.
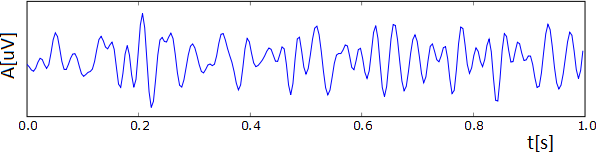
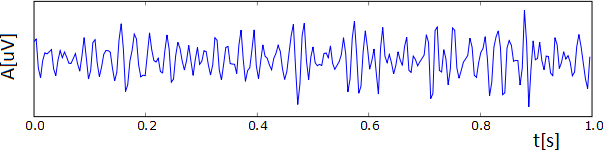
Rytm [math]\alpha [/math]
Fala alfa to jedna z najwcześniej zaobserwowanych struktur (grafoelementów) EEG. Reprezentuje ona rytmiczną aktywność kory mózgowej w paśmie 8-12 Hz. Występowanie rytmu alfa przypisuje się stanowi relaksu z zamkniętymi oczami. Fale alfa najlepiej widoczne są w odprowadzeniach potylicznych, czyli z okolic kory odpowiadającej za przetwarzanie informacji wzrokowych. Rytm o częstości w paśmie alfa rejestrowany w okolicach kory motorycznej nazywany jest rytmem mi (ang. mu), ze względu na kształt fali przypominającej literę μ. Wykazuje on istotny zanik w momencie wykonywania ruchu przez człowieka lub tylko zamierzenia jego wykonania.
Rytm alfa fundamentalne znaczenie w analizie EEG snu. Mimo, że nie występuje podczas właściwego snu to świadczy o „przedsennym” czuwaniu pacjenta, a jej zanik oznacza przejście ze stanu czuwania do płytkiego snu. Fale alfa zanikają także podczas wysiłku umysłowego, np. wykonywaniu działań matematycznych albo przy otwarciu oczu i zadziałaniu na nie światła. Blokowanie rytmu alfa jest wyrazem desynchronizacji aktywności neuronów, zachodzącej pod wpływem koncentracji umysłowej lub stymulacji narządów zmysłów. Przebieg fali alfa zaprezentowano na rysunku 3 i rysunku 4
Cechy charakterystyczne:
- Podstawowy rytm prawidłowego zapisu EEG u dorosłej osoby.
- Quasi harmoniczny przebieg o częstości 7-13 Hz.
- Wzrost amplitudy po zamknięciu oczu, w stanie relaksu czy czuwania z zamkniętymi oczami.
- Zanika po otwarciu oczu.
- Fale alfa najlepiej widoczne są w odprowadzeniach tylnych, czyli z okolic części kory odpowiadającej za przetwarzanie informacji wzrokowych. Czasem jednak może propagować się w kierunku obszarów tylno skroniowych i ciemieniowych.
- Występuje mniej lub bardziej symetrycznie względem płaszczyzny strzałkowej, zwykle jednak ma większą amplitudę nad półkulą dominującą. Zbyt duża asymetria amplitudy rytmu alfa lub też jego brak po jednej stronie zawsze świadczy o jakiejś patologii. Często jednak przyczyną takiej asymetrii jest niewłaściwe umieszczenie elektrod na głowie bądź budowa anatomiczna czaszki.
Cechy patologiczne:
- Częstość rytmu ulega zmniejszeniu pod wpływem takich czynników jak: choroby metaboliczne, wczesne fazy otępienia, leki.
Rytm μ
Cechy charakterystyczne:
- Rytmiczny przebieg o częstości od 7-11 Hz, z uwagi na co często mylony z rytmem alfa.
- Wyraźny przebieg, kształtem przypominający grecką literę μ.
- Zanika w trakcie wykonywania ruchu bądź nawet pod wpływem samego jego wyobrażenia.
Rytm [math]\beta [/math]
Fale beta (rys. %i 5) to niskoamplitudowe oscylacje o częstości w przedziale 13-30 Hz. W paśmie beta wyróżnia się następujące przedziały: wolne fale beta (12-15 Hz), właściwe, średnie pasmo beta (15-18 Hz) i szybkie fale beta, o częstości powyżej 19 Hz. Ta mało zsynchronizowana praca neuronów charakteryzuje zwykłą codzienną aktywność kory mózgowej u człowieka, percepcję zmysłową i pracę umysłową. Specyficzna aktywność beta towarzyszy również stanom po zażyciu niektórych leków. Fale beta zazwyczaj występują w okolicy czołowej. Obrazują one zaangażowanie kory mózgowej w aktywność poznawczą. Fale beta o małej amplitudzie występują podczas koncentracji uwagi, gdy mózg nastawiony jest na świadomy odbiór bodźców zewnętrznych za pomocą wszystkich zmysłów. Cechy charakterystyczne:
- Rytmiczny przebieg o częstości od 13 do 30 Hz.
- Amplituda nie zmienia się pod wpływem otwarcia lub zamknięcia oczu.
- Najwyższa amplituda w okolicach czołowo-centralnych.
- Asymetryczny zanik rytmu w trakcie wykonywania ruchu lub nawet jego wyobrażenia. Zanik obserwowalny jest w zapisie EEG z elektrod umieszczonych nad obszarami mózgu odpowiedzialnymi za kończynę wykonującą ruch (kontralatralnie czyli po przeciwnej stronie niż kończyna).
Fale [math]\gamma [/math]
Fale gamma (rys. %i 6) to fale mózgowe o częstości w okolicach 40 Hz (30-80 Hz). Aktywność w paśmie 80-200 Hz określa się natomiast jako wysokoczęstotliwościową (ang. high) gammę. Rytm gamma towarzyszy aktywności ruchowej i funkcjom motorycznym. Fale gamma związane są też z wyższymi procesami poznawczymi, m. in. percepcją sensoryczną, pamięcią. Przypuszcza się, że rytm gamma o częstotliwości około 40 Hz ma związek ze świadomością percepcyjną (dotyczącą wrażeń zmysłowych i ich postrzegania) oraz związany jest z integracją poszczególnych modalności zmysłowych w jeden spostrzegany obiekt. Aktywność high-gamma występuje podczas aktywacji kory mózgowej, zarówno przez bodźce zewnętrzne (np. dotykowe, wzrokowe), jak i wewnętrzne (przygotowanie ruchu, mowa). Fale o częstościach 100-250 Hz nazywane są ripples. Rejestruje się je w sygnale z implantowanych mikroelektrod, a wysoko częstościową aktywność fast ripples (250-600 Hz) w szczególności u pacjentów z epilepsją, w obszarze ogniska epileptycznego.
Wrzeciona snu
Wrzeciona snu (ang. sleep spindles) (rys. %i 9) to charakterystyczne struktury zaobserwowane już niemal od samych początków historii pomiarów EEG. Występują podczas umiarkowanie głębokiego snu. Wrzecionami snu nazywamy aktywność o częstości 11-15 Hz i czasie trwania 0,5-1,5 s. Obwiednia tych krótkich salw dość szybkiej aktywności o niewielkiej amplitudzie przypomina kształt wrzeciona. Wrzeciona pojawiają się we wszystkich odprowadzeniach, z tym, że ich amplituda i częstość może się nieznacznie zmieniać przy przejściu od przodu do tyłu głowy (od wrzecion „wolnych” po „szybkie”). Wrzeciona snu mogą występować w parach z kompleksami K.
Kompleksy K
Kompleksy K (ang. K-complexes, w Polsce często nazywane zespołami K), (rys. %i 9) mogą pojawiać się pojedynczo lub też w serii po dwa podczas umiarkowanie głębokiego snu. Definiuje się je jako dwufazową (ostry spadek poprzedzony dodatnim maksimum), wysokonapięciową (to największe maksimum strefy), nisko częstotliwościową falę związaną z wrzecionami snu, przy czym jej czas trwania powinien przekraczać 0,5 s. Obecnie wymaga się aby struktury te miały częstość 1-4 cykli/s, amplitudę co najmniej dwa razy większą od średniej amplitudy tła i czas trwania 0,5-2 s. Amplituda kompleksu K jest zazwyczaj największa na czubku głowy. Kompleksy K mogą podczas snu występować spontanicznie lub też w odpowiedzi na bodźce.
Fale piłokształtne
Fale piłokształtne (ang. sawtooth waves) pojawiają się w EEG w czasie snu w fazie REM, są to wierzchołkowe, ujemne fale o umiarkowanej częstości i amplitudzie. Z definicji falą piłokształtną nazywa się pojedyncze lub zgrupowane po kilka fale o częstości 6-10 Hz, amplitudzie rzędu kilkudziesięciu μV i wyraźnym kształcie zębów piły.
Wierzchołkowe fale ostre
Wierzchołkowe fale ostre (ang. vertex sharp waves) występują pod koniec okresu płytkiego snu. Aktywnością tą określa się ostry potencjał, maksymalny w okolicy wierzchołkowej, ujemny w stosunku do innych pól, o amplitudzie zmiennej, rozpiętości często dochodzącej do 250 μV.
Iglice
Iglice (ang. spikes), to termin ograniczony do padaczkopodobnych wyładowań, obserwowanych także w zapisie międzynapadowym EEG. Są to grafoelementy wyraźnie wyróżniające się z czynności podstawowej, z ostrym wierzchołkiem i często następującą po nim falą wolną. Czas trwania iglicy wynosi zazwyczaj od 20 do 70 milisekund, a amplituda co najmniej dwa razy większa o od amplitudy tła w obrębie około 5 sekund.
Artefakty
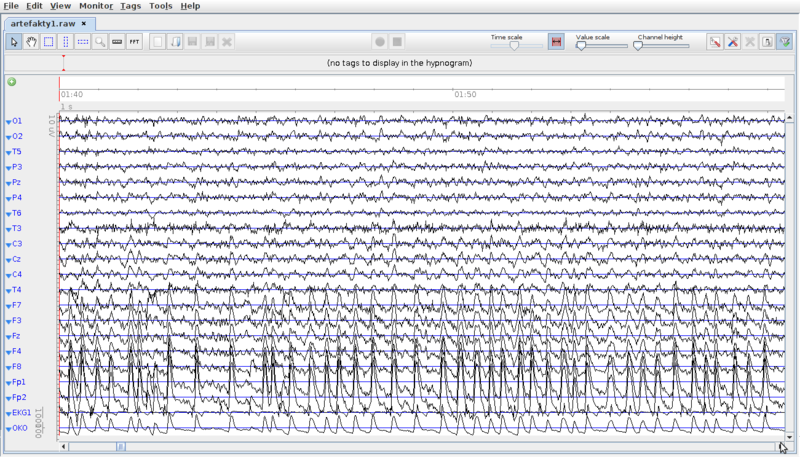
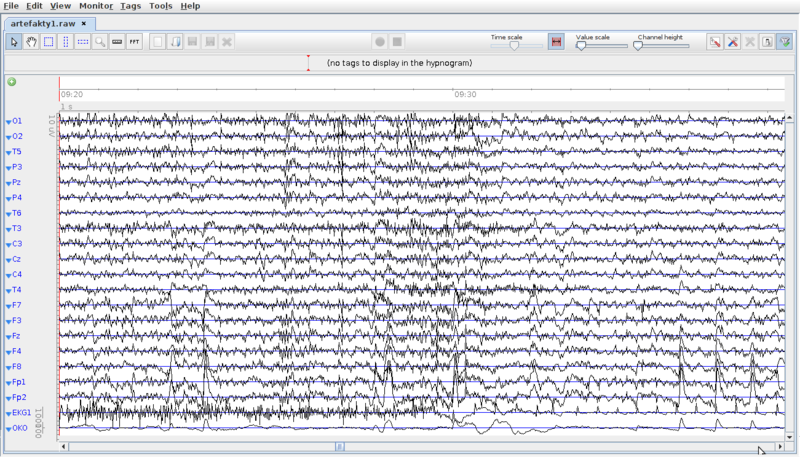
Niewłaściwie umocowanie elektrod
Jednym z bardzo ważnych etapów przed wykonaniem rejestracji czynności elektrycznej mózgu jest umieszczenie na powierzchni głowy elektrod pomiarowych. Elektrody te powinny być rozlokowane zgodnie z wybranym uprzednio standardem (np. 10-20, czy 10-10). Lokalizacja elektrod w badaniu EEG była tematem IX spotkania na Pracowni Sygnałów Bioelektrycznych i nie będzie omawiana już w bieżących materiałach. W tym miejscu zapoznamy się bliżej z konsekwencjami nieprawidłowego umocowania elektrod na głowie badanej osoby. Jak wiemy, poszczególnym obszarom kory mózgowej można przypisać aktywność związaną z określoną czynnością behawioralną, np. w trakcie czuwania z zamkniętymi oczami, w płatach potylicznych powstaje rytmiczna czynność o częstości 7-13 Hz. Z kolei w trakcie planowania bądź wykonywania ruchu zachodzą zmiany w czynności elektrycznej mózgu w obszarach bruzdy Rolanda, nad którą zlokalizowane są miejsca przyłożenia elektrod C3, Cz i C4. Czynność elektryczna mózgu jest bardzo słaba (zwykle wynosi od kliku do kilkudziesięciu μV) i szybko zanika wraz z odległością. Elektroda umieszczona w niewłaściwym miejscu (np. przesunięta o 1 cm względem prawidłowego położenia), nie będzie rejestrować interesującej nas czynności elektrycznej mózgu. Kolejna bardzo istotna kwestia, to przygotowanie skóry w miejscu przyłożenia elektrody. Najbardziej zewnętrzna cześć skóry — naskórek, jest martwy, zrogowaciały i pokryty tłuszczem. Powoduje to, iż opór elektryczny skóry jest bardzo duży (rzędu MΩ) i uniemożliwia rejestrację EEG. Pomiar tego sygnału nie może bowiem odbywać się na drodze „radiowej”, to jest np. za pomocą elektrody umieszczone w pewnej odległości od powierzchni głowy. Wynika to z warunków brzegowych dla pola elektrycznego na granicy ośrodka przewodzącego i próżni.
Podsumowując, rejestracja sygnału EEG wymaga dobrego kontaktu elektrod ze skórą pacjenta, umożliwiającego przewodzenie prądów elektrycznych, będących wynikiem elektrycznej aktywności mózgu. W szczególności dotyczy to tzw. elektrody GND oraz referencyjnej. Niewłaściwe umocowanie tych elektrod na powierzchni głowy będzie skutkować zakłóceniem pomiaru na wszystkich elektrodach. Odpowiednie schematy połączeń elektrod ze wzmacniaczem EEG znajdują się w skrypcie o EEG. Brak dobrego kontaktu powoduje następujące efekty uboczne:
- Tłumienie sygnału (patrz wzór na zajęciach z Pracowni Sygnałów Bioelektrycznych).
- Zakłócanie pomiaru EEG przez pole elektryczne od sieci zasilającej, widoczne w postaci harmonicznego sygnału o częstości 50 Hz i relatywnie wysokiej amplitudzie w porównaniu z amplitudą sygnału EEG.
- „Trzaskanie elektrod”. Polega ono na krótkotrwałym braku kontaktu części elektrody ze skórą. Powoduje to nagłą zmianę potencjału, kształtem przypominającego wyładowania iglicowe, które pełnią ważną rolę w diagnostyce padaczki. Cechą odróżniającą skoki potencjału związane z patologią czynności elektrycznej mózgu, a nieszczelnym kontaktem elektrody ze skórą jest fakt, iż wyładowania związane z niewłaściwym umocowaniem elektrody są widoczne na:
- jednym (uszkodzonym) odprowadzeniu w przypadku odprowadzeń referencyjnych jednobiegunowych;
- dwóch elektrodach w przypadku odprowadzeń dwubiegunowych.
Jeśli zmiana kontaktu ze skórą nie ma gwałtownego charakteru, niewłaściwie zamocowana elektroda może być źródłem powstawania zmian potencjału w zakresie pasm EEG, trudno odróżnialnych od prawdziwej czynności elektrycznej. Jedyną cechą różnicującą ten artefakt od sygnału EEG jest fakt jego występowania na pojedynczej elektrodzie, w przypadku odprowadzeń jednobiegunowych i dwóch sąsiednich kanałach, będących lustrzanymi odbiciami w przypadku odprowadzeń dwubiegunowych.
Pocenie się
Pocenie się badanej osoby prowadzi do:
- Rozpuszczania klejów wodozmywalnych, za pomocą których elektrody przyczepiane są do powierzchni głowy. Pogarsza to kontakt elektrody ze skórą.
- Tworzenie zwarć pomiędzy elektrodami. Pot składający głównie z wody, soli i innych związków chemicznych dobrze przewodzi prąd. W efekcie następuje redukcja impedancji pomiędzy elektrodami i zmiana wartości mierzonego potencjału.
Wymienione powyżej zjawiska prowadzą do powstania w zapisie EEG bardzo wolnych, trwających kilka sekund fal.
Mruganie
Bardzo silny artefakt, trudny do wyeliminowania z zapisu EEG, mogący się objawić na wszystkich elektrodach, w szczególności zaś widoczny na odprowadzeniach przedczołowych i czołowych. Źródłem tego artefaktu jest występująca pomiędzy rogówką a siatkówką różnica potencjałów (sięgająca wartości kilku miliwotlów) oraz czynność elektryczna siatkówki o amplitudzie kilku mikrowoltów. W trakcie mrugania gałki oczne skręcają nieznacznie ku górze (tzw. zjawisko Bella) powodując nagły wzrost potencjału elektrycznego. Rogówka posiada potencjał dodatni względem siatkówki, w związku z czym na odprowadzeniach przedczołowych i czołowych obserwuje się wychylenie potencjału w kierunku dodatnich wartości względem potencjału na innych elektrodach. Zwiększony potencjał na elektrodach czołowych utrzymuje się tak długo, jak skręcone ku górze pozostają gałki oczne. Powrót gałek do pozycji spoczynkowej powoduje redukcję potencjału na przednich elektrodach. Zmiana sygnału związana z artefaktem od gałki ocznej ma zatem charakter „schodka”, jednakże filtry w które wyposażony jest wzmacniacz EEG powodują rozmycie i wygładzenie tego zaburzenia, które przyjmuje łatwo rozpoznawalny kształt. Artefakt ten jest na tyle silny, iż pomimo losowego występowania, uśrednianie sygnałów EEG mierzonych w trakcie powtarzania tego samego paradygmatu doświadczalnego nie redukuje jego amplitudy w sposób zadowalający. Środkami mogącymi zmniejszyć jego występowanie jest przewidzenie w trakcie eksperymentu przerw na „wymruganie”, używanie środków nawilżających oczy (najlepiej w postaci żeli, które długo pozostają na gałce), lekkie zmrużenie oczu.
Ruchy gałek ocznych na boki
Źródło powstawania tych artefaktów jest takie samo jak w przypadku mrugania. W wyniku różnic potencjałów pomiędzy siatkówką a rogówką, zmiana orientacji gałki ocznej w przestrzeni powoduje zmianę pola elektrycznego i jego potencjału, który mierzymy. W przypadku skręcenia oczami w prawą stronę, nastąpi wzrost mierzonego potencjału na elektrodzie skroniowej prawej — F8 (dodatnio naładowana część gałki przybliża się do tej elektrody) i jego spadek na elektrodzie leżącej po przeciwnej stronie głowy — F7 (dodatnio naładowana część gałki odsuwa się do tej elektrody). Dzięki temu artefakt ten jest łatwo rozpoznawalny. U osób z oczopląsem artefakt ten występuje rytmicznie z częstością oczopląsu. Należy również pamiętać, że ruchy gałek ocznych są sterowane mięśniami, w związku z czym nagłe i silne ruchu gałek na boki będą powodowały występowanie wyładowań iglicowych związanych z czynnością mięśni. Amplituda tych wyładowań osiągnie największą wartość na elektrodach F8 i F7.
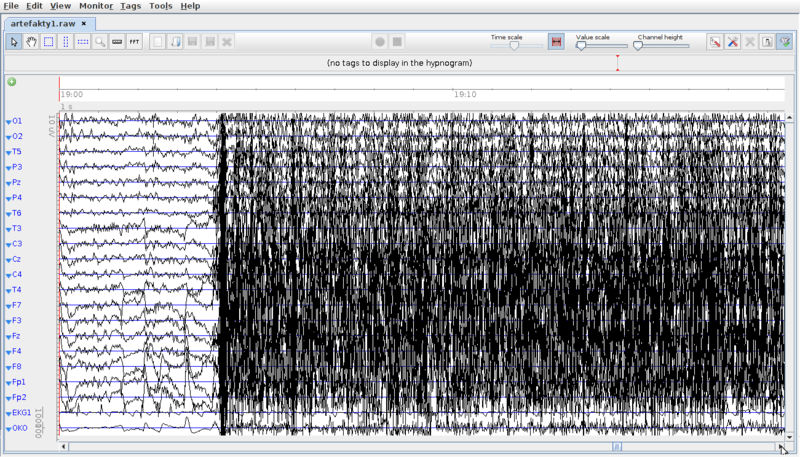
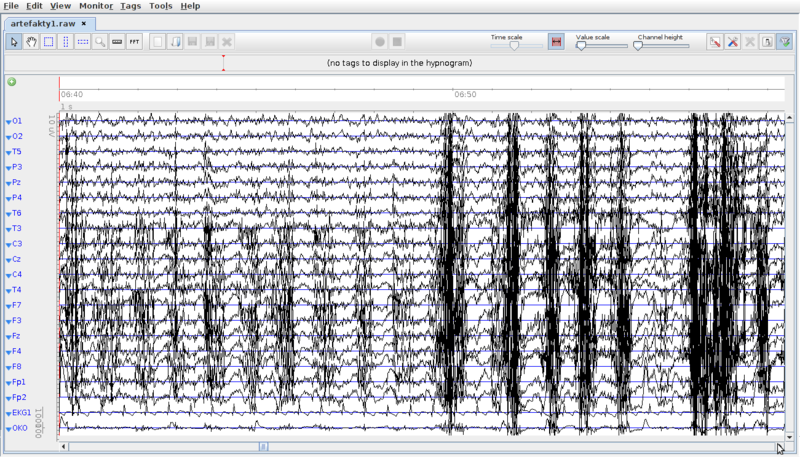
Elektryczna Czynność Mięśni — EMG
Na głowie człowieka znajdują się mięśnie, bądź przyczepy mięśni odpowiedzialnych głównie za mimikę twarzy, ruchy gałek ocznych czy ruchy szczęki. W związku z powyższym artefakty mięśniowe najsilniej będą rejestrowane przez elektrody czołowe oraz skroniowe (przednie i środkowe). Artefakty te są znaczne silniejsze niż zapis EEG (mogą dochodzić do kilku mV), zaś ich widmo w niskich częstościach pokrywa się z pasmem beta i gamma w EEG. Powstawaniu artefaktów EMG sprzyja: niewłaściwe oświetlenie laboratorium (co powoduje mrużenie oczu), niewygodna dla pacjenta pozycja — brak oparcia dla głowy, brak oparcia dla rąk i nóg, wykonywane testy wymagające uwagi i koncentracji. W tym ostatnim przypadku, w trakcie rozwiązywania takiego testu, cześć spośród badanych osób ma tendencję do marszczenia czoła, czy mrużenia oczu.
Czynność elektryczna serca
Artefakt ten pojawia się najczęściej rytmicznie wraz z czynnością elektryczną serca i przyjmuje charakterystyczny dla niego kształt. Zdarza się jednak, że nie każdy kolejny cykl pracy serca zostanie zmierzony przez elektrody EEG. Wtedy artefakt ten może być pomylony z wyładowaniami iglicowymi. Najlepszą metodą detekcji tego artefaktu jest jednoczesny pomiar EEG i EKG. Zakłócenie związane z EKG objawia się najsilniej na elektrodzie, które została umieszczona tuż nad jakąś tętniczką. Często to ma miejsce w przypadku gdy jako elektrodę referencyjną wybrano elektrodę umieszczoną na wyrostku sutkowatym (za uszami), gdzie u wielu osób przebiega właśnie mała tętniczka. Sygnały z kanałów referencyjnych odejmowane są od sygnałów zarejestrowanych od pozostałych kanałów co będzie w oczywisty sposób prowadzić do „rozpowszechniania się” artefaktu EKG po wszystkich elektrodach. O ile to możliwe, należy zmienić nieznacznie pozycję elektrody, tak aby nie znajdowała się ona nad tętniczką.
Żucie, ruchy języka
Artefakt związany z żuciem to głównie potencjały od czynności elektrycznej mięśni o częstości występowania skorelowanej z rytmicznie powtarzającym się ruchem szczęk. Z kolei ruch języka powoduje również czynność elektryczną ale nie mającą charakteru rytmicznego, przypominającą fale delta.
Drżenie kończyn
Drżenie kończyn może być spowodowane chorobą (np. Parkinsona) lub długotrwałym siedzeniem w mało komfortowej pozycji. Ruchy kończyn będą wywoływały także ledwo zauważalne ruchy głowy. W sytuacji, gdy badana osoba cierpi na chorobę Parkinsona, drżenia kończyn prowadzą do powstania rytmicznej fali o częstości 5-6 Hz przypominającej wyładowania padaczkowe. W celu lepszej detekcji tego artefaktu wskazane jest rejestrowanie czynności EMG.
Chodzenie osób w pobliżu badanego
Chodzenie w pobliżu badanej osoby powoduje powstawanie artefaktu przypominającego fale ostre.
Artefakty związane z ruchem badanej osoby.
Wywołane są dowolnymi ruchami głowy i ciała badanej osoby i związaną z nimi czynnością elektryczną mięśni. Powstałe potencjały są szerokopasmowe i mają znaczne amplitudy. Ruchy badanej osoby prowadzą do:
- ruchu elektrod, a w związku tym pogorszenia ich kontaktu ze skór, a nawet oderwania elektrod od skóry;
- zmiany strumienia pola elektromagnetycznego przechodzącego przez pętle utworzone przez elektrody i wzmacniacz. Zgodnie z prawem indukcji Faradaya, zmiana strumienia w czasie spowoduje powstaje siły elektromotorycznej.
Redukcja artefaktów
Kilka rad umożliwiających redukcję artefaktów, bądź ich lepsze rozpoznanie:
- zadbać o położenie wzmacniacza EEG z dala od innych urządzeń i kabli. Umieścić go na podkładce z tworzywa;
- zadbać o komfortową pozycję dla pacjenta;
- mierzyć czynność EKG, EMG i elektrookulogram wraz z EEG;
- sporządzać notatki na temat zachowania się pacjenta (jeśli mamy możliwość obserwowania go) — kiedy się poruszał, czy ktoś do niego podszedł np. celem poprawienia jakiegoś elementu układu eksperymentalnego.
Ćwiczenia
Ćwiczenie I: rejestracja EEG z artefaktami oraz EEG spoczynkowego
- Przypomnij sobie:
- procedurę zakładania czepka na głowie
- przygotowanie skóry głowy
- techniczne uwagi dotyczące pomiaru EEG.
-
Dokonaj przynajmniej 25-minutowego zapisu EEG w systemie 10-20, jako elektrody referencyjne wybierz elektrody uszne. Jednocześnie wraz z rejestracją EEG dokonaj pomiaru sygnału EKG z odprowadzenia I Einthovena, EMG z szyi oraz elektrookulogamu. W trakcie pomiaru, w wybranych chwilach czasu wykonaj:
- mrugnięcie,
- ruch językiem,
- żucie,
- napięcie mięśni rąk bądź nóg na tyle silne, aby wywołało drżenie,
- ruch oczu w prawo,
- ruch oczu w lewo,
- zmarszczenie czoła,
- zaciśnięcie zębów,
- napięcie mięśni szyi,
- ruch głową
Wszystkie powyższe czynności powinny być odseparowane od siebie w czasie. Osoba biorąca razem z Tobą udział w eksperymencie powinna dokładnie zanotować moment wykonywania przez Ciebie kolejnych ruchów. Następnie, poproś kolegę aby:
- przez 30 sekund chodził za Tobą,
- pogłaskał Cię po ramieniu
Kolega powinien odnotować czas wykonywania powyższych czynności. Po zakończeniu rejestracji otwórz z pliku zapisany sygnał. Obejrzyj dokładnie zarówno 2-minutowe odcinki sygnału pomiędzy wykonywanymi ruchami jak i w momencie wykonywania ruchów. Scharakteryzuj powstałe artefakty pod względem amplitudy, długości trwania, widma mocy i topografii. Zmień referencje pomiaru z jednobiegunowego usznego na dwubiegunowy podłużny bananowy. Ponownie przyjrzyj się zapisowi i scharakteryzuj artefakty.
- Ponownie dokonaj przynajmniej 25-minutowego zapisu EEG wraz z EMG, EKG i elektrogokulogramem. Powtórz wszystkie czynności ruchowe wymienione w poprzednim punkcie. Zanotuj czas wystąpienia danego ruchu, ale nie ujawniaj go nikomu. Swój zapis sygnałów bioelektrycznych przekaż pozostałym grupom. Od nich otrzymasz również zapisy. Na podstawie dotychczas zebranych wiadomości, dokonaj przeglądu otrzymanych zapisów pod kątem występowania artefaktów. Pod dokonaniu analizy poproś grupy od których otrzymałeś dane o informacje jakie ruchy były wykonywane w określonej chwili czasu. Sprawdź poprawność dokonanych przez Ciebie oznaczeń artefaktów z informacjami dostarczonymi przez kolegów.
- Zarejestruj 10 minut sygnału EEG, w trakcie których badana osoba będzie siedziała z otwartymi oczami oraz kolejne 10 minut w stanie czuwania z zamkniętymi oczami.
Ćwiczenie II — Estymacja funkcji autokowariancji, autokorelacji i koherencji sygnału.
Zadanie 1: Funkcje autokowariancji i autokorelacji
Wstęp
Z funkcjami tymi spotkaliśmy się już na zajęciach z analizy sygnałów.
Funkcja autokowariancji sygnału charakteryzuje liniową zależność wartości tego sygnału w danej określonej chwili czasu od wartości (tego samego sygnału) w innej chwili. W przypadku stacjonarnych procesów stochastycznych, przebieg tej funkcji nie zależy od czasu. Oznacza to, że obliczając funkcję autokorelacji sygnału pomiędzy chwilą czasu [math]x(t)[/math] i [math]x(t+\tau )[/math] otrzymamy tę samą wartość, jak dla przypadku obliczania funkcji autokorelacji pomiędzy momentami [math]x(t + T)[/math] i [math]x(t + T+\tau )[/math], gdzie [math]T[/math] to dowolny przedział czasu. Innymi słowy, funkcja autokorelacji procesu stacjonarnego zależy tylko od odstępu czasu pomiędzy próbkami [math]\tau[/math], dla którego jest wyznaczana, a nie od konkretnej chwili czasu. Odrębną klasę sygnałów stanowią procesy niestacjonarne, w przypadku których funkcja autokorelacji będzie zależeć od czasu [math]t[/math] w którym jest obliczana. Estymator funkcji autokowariancji uzyskuje się poprzez obliczanie iloczynów wartości sygnału [math]x[/math] w chwilach czasu [math]t[/math] czyli [math]x(t)[/math] i wartości sygnału [math]x[/math] w chwili czasu t+τ czyli [math]x(t+\tau)[/math] i uśredniając wartości iloczynów po czasie [math]T[/math]:
gdzie:
W przypadku sygnałów ciągłych estymację tę można zapisać w poniższy sposób:
natomiast dla sygnałów dyskretnych jako:
gdzie:
Funkcja autokowariancji może osiągać dowolne wartości, dlatego aby można było porównać przebieg tej funkcji np. pomiędzy dwoma sygnałami, wprowadzono wersję znormalizowaną tej funkcji - funkcję autokorelacji. Normalizacja ta wygląda następująco:
gdzie:
Wariancję sygnału ([math]\gamma (0)=\sigma ^2[/math]) można wyrazić przez funkcję autokowariancji dla przesunięcia [math]\tau =0[/math]. Wynika z tego, że funkcja korelacji przyjmuje wartości z zakresu [math][-1, \, 1][/math]. Ostatecznie estymator funkcji autokorelacji można zapisać jak poniżej:
Funkcję autokorelacji estymuje się w celu określenia, w jakim stopniu wartości sygnału w danej chwili czasu wpływają na wartości sygnału w kolejnych chwilach czasu. Ma to kluczowe znaczenie przy rozpoznawaniu rodzaju procesów fizycznych odpowiedzialnego za generowanie sygnału. Funkcja ta zawsze mam maksimum dla przesunięcia [math]\tau =0[/math].
Cechą charakterystyczną funkcji autokorelacji jest to, iż w przypadku sygnałów harmonicznych, przebieg funkcji ma charakter okresowy, z okresem takim samym o okres badanego sygnału. W przypadku szumu, funkcja autokorelacji ma kształt funkcji delta Diraca.
Polecenie:
Zaimplementuj funkcję do oblicznia funkcji korelacji zgodnie ze wzorem (4). Funkcja powinna przyjmować dwa wektory i maksymalne przesunięcie wzajemne tych wektorów, natomiast zwracać powinna wektor zawierający funkcję autokorelacji. Wywołanie przykładowe:
a = np.array([1,2,3])
print koreluj(a,a,2)
powinno dać wynik:
[-0.5 0. 1. 0. -0.5]
W tym zadaniu posłużymy się sygnałami zarejestrowanymi w punkcie 4. poprzedniego ćwiczenia. Zaobserwuj, na którym kanale rytm alfa osiąga najwyższą wartość. Następnie zaimplementuj w Pythonie następujące kroki:
- Wczytaj dane z wybranego kanału.
- Oblicz funkcję autokorelacji dla sygnału zarejestrowanego w warunkach, gdy osoba badana siedziała z otwartymi oczami. Narysuj autokorelogram, to jest wykres wartości funkcji autokorelacji względem przesunięcia [math]\tau [/math]. Oś [math]\tau [/math] wyskaluj w sekundach.
- Powtórz krok 2, tym razem za sygnału zebranego w warunkach czuwania z zamkniętymi oczami.
- Porównaj autokorelogramy.
Zadanie 2: Związek autokorelacji z widmem sygnału
Wstęp
Zgodnie z twierdzeniem Chinczyna, z którym zapoznaliśmy się na wykładzie z Analizy Sygnałów, widmową gęstość mocy sygnału można policzyć jako transformatę Fouriera funkcji autokowariancji:
gdzie:
- [math]f[/math] — częstość
- [math]S(f)[/math] — gęstość widmowa mocy
Polecenie:
Oblicz gęstość widmową mocy sygnału zarejestrowanego w trakcie czuwania z zamkniętymi oczami, korzystając z twierdzenia Chinczyna oraz metodą Welcha. Znajdź częstość rytmu [math]\alpha[/math] dla osoby, która była badana.
Zadanie 3: Funkcja kowariancji i korelacji
Wstęp
W celu scharakteryzowania zależności wzajemnej dwóch sygnałów losowych, stosuje się funkcję kowariancji, zdefiniowaną w następujący sposób:
gdzie:
W przypadku sygnałów ciągłych estymację tę można zapisać w poniższy sposób:
natomiast dla sygnałów dyskretnych jako:
W odróżnieniu od funkcji autokowariancji, funkcja kowariancji nie musi mieć maksimum dla przesunięcia [math]\tau =0[/math]. Ponadto posiada ona następującą cechę:
Funkcję kowariancji można znormalizować:
Otrzymaną funkcję nazywamy funkcją korelacji. Jednym z zastosowań funkcji korelacji jest wyznaczanie czasu przejścia sygnału przez dany układ liniowy. Funkcja korelacji pomiędzy sygnałem na wejściu układu i sygnałem na jego wyjściu osiągnie wartość maksymalną dla przesunięcia [math]\tau [/math] równego czasowi, jaki potrzebował sygnał na pokonanie danego układu. Niestety, taka metoda wyznaczania opóźnienia obarczona jest pewną wadą — w przypadku gdy prędkość sygnału bądź jego droga zależą od częstości, wtedy na wykresie funkcji korelacji nie uzyskamy wyraźnego maksimum.
Polecenie
Zaimplementuj funkcję obliczającą funkcję kowariancji dla różnych sygnałów x i y (równanie 13) skorzystaj przy tym z własności opisanej równaniem (14). Przykładowe wywołanie:
a = np.array([1,2,3])
b = np.array([-1,-2,-3])
print koreluj(a,b,2)
powinno dać w wyniku:
[ 0.5 0. -1. 0. 0.5]
Z danych zarejestrowanych w trakcie czuwania z zamkniętymi oczami wybierz sygnały z następujących kanałów: Fp1, P3, Pz, P4, Fp2, O1, O2.
- Dla każdego kanału oblicz funkcję autokorelacji, zaś dla każdej pary kanałów oblicz funkcję korelacji wzajemnej. Wyniki zaprezentuj w formie kwadratowej macierzy wykresów (za pomocą funkcji subplot, tak jak na przykładowym rys. (rys. %i 10)). Na przekątnej macierzy narysuj funkcję autokorelacji odpowiednich kanałów, poza przekątną — funkcję korelacji wzajemnej. Wskaż kanały, które są najbardziej skorelowane ze sobą. Czy możliwe jest wyznaczenie opóźnienia sygnału pomiędzy tymi kanałami?
- Powtórz punkt 1, tym razem jednak funkcję autokorelacji i korelacji wzajemnej oblicz na sygnałach przefiltrowanych filtrem wąskopasmowym w paśmie alfa charakterystycznym dla badanej osoby. (przypomnienie konstrukcji filtrów)
-
Oszacuj istotność statystyczną zależności między parami kanałów. Twoją hipotezą zerową jest brak istotnej korelacji pomiędzy sygnałami zarejestrowanymi przez dwie różne elektrody EEG. Hipoteza alternatywna to występowanie zależności pomiędzy tymi sygnałami. Podanie estymatorów wariancji funkcji korelacji jest bardzo trudne, dlatego jednym ze sposobów oszacowania progu powyżej którego wartość funkcji korelacji można byłoby uznać za istotną statystycznie, jest zastosowanie metody bootstrap. Teoretycznie, funkcja korelacji policzona dla dwóch rzeczywistych, nieskorelowanych sygnałów, powinna wynosić 0 dla każdego przesunięcia [math]\tau[/math]. Tak jest jednak w przypadku sygnałów nieskończonych; w analizie sygnałów takowych nie spotkamy.
Dokonując losowej zamiany kolejności próbek, możemy doprowadzić do wytworzenia sygnałów zależnych losowo, które jednak ze względu na skończony czas trwania, dadzą niezerową funkcję korelacji. Poziom losowych fluktuacji tej funkcji oszacujemy wykonując następujące kroki:
- Losowa zamiana kolejności próbek w analizowanych sygnałach. Jeżeli pomiędzy dwoma sygnałami istnieją jakieś zależności, losowa zamiana próbek doprowadzi do zniszczenia tych związków. W ten sposób uzyskujemy sygnały, które teoretycznie są nieskorelowane.
- Obliczenie funkcji korelacji wzajemnej dla sygnałów policzonych w punkcie A.
- Powtórzenie kroków A i B wiele (np. 1000) razy.
- Oszacowanie 95 % przedziału ufności dla wartości średniej funkcji korelacji wzajemnej dla danego przesunięcia [math]\tau[/math] korzystając z otrzymanego w kroku C empirycznego rozkładu wartości tych funkcji dla sygnałów niezależnych.
- Powtórzenie kroków A-D dla kolejnych przesunięć [math]\tau[/math].
- Sprawdzenie, dla których przesunięć [math]\tau [/math] funkcje autokorelacji i korelacji obliczone dla oryginalnych sygnałów uzyskały wartości wyższe niż wartości progowe oszacowane dla sygnałów o losowych zależnościach.
Procedura opisana powyżej ma jednak pewną wadę. Staramy się w niej oszacować poziom przypadkowych korelacji pomiędzy dwoma sygnałami dla kolejnych przesunięć [math]\tau [/math], co jest niczym innym jak wielokrotnym powtórzeniem pewnego testu. Obserwowanie korelacji dla wielu par kanałów równocześnie również prowadzi do zwiększenia szansy na zaobserwowanie ekstremalnie dużych fluktuacji. Występuje tu zatem problem wielokrotnych porównań. Przypominamy, iż może to doprowadzić do przypadkowego uznania wyników jako „istotnych” statystycznie. Np. jeśli pojedynczy test wykonujemy na poziomie istotności 5% to dopuszczamy odrzucenie w 1 przypadku na 20 hipotezy zerowej pomimo, iż jest ona prawdziwa. Z drugiej jednak strony, jeśli powtórzymy wykonywany test 20 razy, to oczekujemy uzyskania 1 przypadku, w którym poziom [math]p[/math] będzie mniejszy od 5% co jest przesłanką za odrzuceniem hipotezy zerowej.
W przypadku wykonywania serii testów należałoby więc zastosować odpowiednie poprawki, np. korektę Bonferroniego czy false discovery rate (FDR). Innym rozwiązaniem w analizowanym przez nas problemie jest zastosowanie tzw. statystyk wartości ekstremalnych, które prowadzą do następujących zmian w procedurze (nie działa dla funkcji autokorelacji ze względu na jej normalizację do 1 dla zerowego przesunięcia):
- Losowa zmiana kolejności próbek w analizowanych sygnałach (we wszystkich analizowanych kanałach). Jeżeli pomiędzy dwoma sygnałami istnieją jakieś zależności, losowa zamiana próbek doprowadzi do zniszczenia tych związków. W ten sposób uzyskujemy sygnały, które teoretycznie są nieskorelowane.
- Obliczenie funkcji korelacji dla sygnałów otrzymanych w punkcie A.
- Zapamiętanie maksymalnej wartości bezwzględnej funkcji korelacji z punktu B (maksimum bierzemy po wszystkich przesunięciach i po wszystkich parach kanałów).
- Powtórzenie kroków A-C 1000 razy. Uzyskamy w ten sposób rozkład maksymalnych wartości funkcji korelacji możliwych do zaobserwowania dla sygnałów niezależnych.
- Wyznaczenie 95 centyla rozkładu wartości maksymalnych.
- Nałożenie na rysunki funkcji korelacji uzyskane w Zadaniu 2 poziomych linii symbolizujących poziom zależności dwóch sygnałów o losowych zależnościach i sprawdzenie, dla których przesunięć [math]\tau [/math] wartości funkcji korelacji przekraczają estymowane progi istotności statystycznej.
Zadanie 4: Wzajemna gęstość widmowa sygnałów i koherencja
Wstęp
Podobnie jak w przypadku twierdzenia Chinczyna dla pojedynczego sygnału, możliwe jest policzenie transformaty Fouriera funkcji kowariancji. Uzyskana w ten sposób wielkość nazywa się funkcją wzajemnej gęstości mocy widmowej sygnału:
W celu dalszego omówienia własności funkcji wzajemnej mocy widmowej sygnałów funkcję tę zapiszemy w postaci:
Wartość bezwzględna funkcji wzajemnej gęstości mocy widmowej osiąga największą wartość dla częstości, w których sygnały [math]x(t)[/math] i [math]y(t)[/math] są ze sobą skorelowane. Funkcja wzajemnej mocy widmowej sygnałów pozbawiona jest zatem wady, która charakteryzowała funkcję korelacji, to jest problemu z wyznaczeniem czasu transmisji sygnału, w przypadku gdy czas ten zależał od częstości. Przy pomocy funkcji wzajemnej mocy widmowej, czas ten można oszacować przy pomocy fazy tej funkcji — [math]\phi _{xy}(f)[/math]. Jeśli funkcja wzajemnej mocy widmowej została wyznaczona pomiędzy sygnałami na wejściu i wyjściu układu liniowego, to faza ta reprezentuje przesunięcie fazowe sygnału przy przejściu przez układ. Czas tego przejścia można oszacować za pomocą następującej wyrażenia:
Podobnie jak w przypadku funkcji autokorelacji i korelacji wzajemnej, funkcję wzajemnej gęstości mocy widmowej można znormalizować:
Znormalizowaną postać funkcji wzajemnej gęstości mocy widmowej nazywamy funkcją koherencji. Koherencja jest wielkością zespoloną. Faza koherencji odzwierciedla różnicę faz pomiędzy dwoma sygnałami. Moduł koherencji reprezentuje stopień synchronizacji sygnałów i zawiera się w przedziale od 0.0 do 1.0. Moduł tej funkcji zawiera się w przedziale od 0 do 1. Wartości 0 odpowiada brak synchronizacji pomiędzy sygnałami, zaś wartości 1 pełna synchronizacja dwóch przebiegów czasowych. Należy również zwrócić uwagę na nazewnictwo - często sam moduł koherencji określany jest jako koherencja, w literaturze anglojęzycznej moduł koherencji posiada jednak odrębną nazwę: Magnitude Square Coherence (MSC). Istotny jest również sposób estymacji modułu koherencji, który wyprowadzono w następnym rozdziale, zaś sam estymator reprezentuje wzór (36).
Kilka słów o koherencji
Wzór (Equation 19), definiujący ilościową miarę koherencji, nie uwzględnia stochastycznego charakteru sygnałów. Łatwo zauważyć, że bezpośrednie zastosowanie tego wzoru do obliczenia koherencji dwóch sygnałów o tej samej częstości i różniących się jedynie amplitudą oraz fazą, zawsze da wynik równy 1. Prześledźmy to na następującym przykładzie.
Dane są dwa sygnały harmoniczne [math]x(t) = A\cos(\Omega t + \phi_x)[/math] oraz [math]y(t) = B\cos(\Omega t + \phi_y)[/math].
Widmo tych sygnałów, wyrażone za pomocą transformaty Fouriera, będzie miało następującą postać:
[math]X(f)=Ae^{-j\phi_x}[/math]
[math]Y(f)=Be^{-j\phi_y}[/math],
zaś ich widmo wzajemne:
[math]X(f)\cdot Y^*(f) = A\cdot Be^{-j(\phi_x - \phi_y)}[/math],
gdzie: [math]j=\sqrt{-1}[/math], a * oznacza sprzężenie liczby zespolonej.
Podstawienie wyrażeń na widmo sygnałów [math]x(t)[/math], [math]y(t)[/math] oraz ich widmo wzajemne do wzoru ??? da koherencję [math]K_{xy}(f) = 1[/math] niezależnie od amplitudy sygnałów [math]A[/math] i [math]B[/math] oraz ich faz [math]\phi_x[/math] i [math]\phi_y[/math].
W praktyce rzadko jednak mamy do czynienia z sygnałami harmonicznymi. Zwykle mierzone przez nas wielkości mają stochastyczny charakter bądź też ich pomiar jest zaburzany przez różne czynniki.
Rozważmy teraz najprostszy model pomiaru sygnału, w którym uwzględniono wpływ zakłóceń w postaci białego szumu. Na wejście układu LTI o funkcji impulsowej opisanej wyrażeniem [math]h(t)[/math] podamy sygnał [math]x(t)[/math] i widmie danym funkcją [math]X(f)[/math]. Układ LTI przetworzy sygnał wejściowy na przebieg [math]y(t)[/math] o widmie [math]Y(f)[/math]. Z uwagi na zaburzenia [math]n(t)[/math] o widmie [math]N(f)[/math] towarzyszące pomiarowi aparatura nie zarejestruje sygnał [math]y(t)[/math] lecz [math]z(t) = y(t) + n(t)[/math]. Opisane zależności możemy opisać za pomocą poniższych wzorów:
[math]y(t) = h(t)*x(t)[/math]
[math]z(t) = y(t) + n(t)[/math]
gdzie: [math]*[/math] - operacja splotu.
Dokonując transformacji powyższych wzorów do dziedziny częstości dostajemy:
[math]Y(f) = H(f)X(f)[/math]
[math]Z(f) = Y(f) + N(f)[/math]
gdzie: [math]H(f) = \textrm{FFT}\left\{h(t)\right\}[/math].
Wzory te można zapisać w postaci jednej zależności:
Załóżmy teraz, że w celu redukcji składowej losowej [math]n(t)[/math] wielokrotnie powtarzamy w tych samych warunkach pomiar sygnału [math]z(t)[/math]. Za każdym razem na wejściu układu LTI występuje ten sam sygnał [math]x(t)[/math]. Układ LTI również przetwarza sygnał wejściowy w ten sam sposób, jednak z uwagi na stochastyczny charakter zakłóceń, otrzymujemy kolejne różniące się do siebie przebiegi [math]z_i(t)[/math]. Niech liczbę powtórzeń pomiaru wynosi [math]K[/math]. Możemy napisać [math]K[/math] równań opisujących relację pomiędzy sygnałem wejściowym, wyjściowym i mierzonym:
Przemnóżmy teraz równania (Equation 21) obustronnie przez sprzężone widmo sygnału rejestrowanego [math]Z(f)[/math]. Dla uproszczenia zapisu operacji dokonamy na jednym, dowolnie wybranym [math]i[/math]-tym równaniu:
Na równaniu (Equation 22) dokonamy kolejno następujących przekształceń:
Dokonajmy teraz uśredniania (Equation 24) po kolejnych powtórzeniach pomiaru.
Zakładamy, że szum [math]N(f)[/math] jest nieskorelowany z sygnałem wejściowym, w związku z czym w wyniku uśredniania dwa ostatnie składniki równania (Equation 25) zostaną zredukowane: [math]\left\langle H(f)X(f)N_i^*(f)\right\rangle \approx 0 [/math], [math]\left\langle N_i(f)H^*(f)X^*(f)\right\rangle \approx 0 [/math]. Założyliśmy również za każdym razem na wejściu układu liniowego pojawia się ten sam sygnał [math]x(t)[/math], sam układ zaś nie zmienia swoich właściwości, w zwiazku z czym: [math]\left\langle|H(f)|^2|X(f)|^2\right\rangle = |H(f)|^2|X(f)|^2 [/math]. Ostatecznie uzyskaliśmy następującą zależność:
Dokonajmy kolejnego przekształcenia równania (Equation 21). tym razem przemnożymy obustronnie każde równanie przez sprzężone widmo sygnału wejściowego. W celu uproszczenia zapisu, operację tę wykonamy tylko na jednym dowolnie wybranym [math]i[/math]-tym równaniu:
,
gdzie: [math]Z_i(f)X^*(f)[/math] - to widmo wzajemne sygnałów [math]x(t)[/math] i [math]y(t)[/math]. Proste przekształcenie równania (Equation 27) prowadzi do następującego wyrażenia:
Uśrednimy teraz równanie (Equation 28) po kolejnych realizacjach pomiaru oraz obliczmy moduł uzyskanego wyniku:
Brak korelacji pomiędzy szumem [math]n(t)[/math] a sygnałem wejściowym [math]x(t)[/math] powoduje, że w wyniku uśredniania zostaje zredukowany drugi składnik równania (Equation 29): [math]\left\langle N_i(f)X^*(f)\right\rangle \approx 0[/math]. Ostatecznie uzyskujemy następującą zależność:
która wraz z równaniem (Equation 26) tworzy układ równań opisujących relacje pomiędzy widmami i widmami mocy sygnałów występujących w naszym modelu:
- [math] \left\langle|Z_i(f)|^2\right\rangle= |H(f)|^2 |X(f)|^2 + \left\langle|N_i(f)|^2\right\rangle [/math]
Z pierwszej zależności równania (Equation 31) wyznaczmy funkcję przejścia [math]|H(f)|[/math]:
[math]|H(f)| = \frac{|\left\langle Z_i(f)X^*(f)\right\rangle|}{|X(f)|^2}[/math]
i podstawy do drugiego równania układu (Equation 31). Otrzymujemy:
Równanie (Equation 32) możemy przekształcić do postaci:
a następnie do zależności:
Wyrażenie:
nazywana jest Magnitude Square Coherence pomiędzy sygnałami [math]x(t)[/math] i [math]z(t)[/math]. W przypadku, gdy wielkość ta jest równa 1 sygnały [math]x(t)[/math] i [math]z(t)[/math] są w pełni zsynchronizowane. Wielkość tę uzyskaliśmy dla sygnału na wejściu układu LTI oraz sygnału mierzonego na wyjściu. Funkcję MSC można jednak stosować do dowolnych dwóch sygnałów stochastycznych [math]x(t)[/math] i [math]y(t)[/math] przy założeniu, że istnieją pomiędzy nimi liniowe zależności:
gdzie: [math]\lt \gt [/math] - oznacza wartość średnia, [math]X_i(f), Y_i(f) [/math] to zespolone widma (policzone np. za pomocą Transformaty Fouriera), wyznaczone odpowiednio dla sygnałów X oraz Y w "i-tej" realizacji eksperymentu lub w "i-tym" oknie czasowym, na który te sygnały zostały podzielone. Wzór (36) reprezentuje estymator wartości bezwzględnej koherencji. Opierając się na podobnym co wyżej rozumowaniu, można wyprowadzić estymator funkcji koherencji, o następującej postaci:
Faza koherencji umożliwia nam estymację przesunięcia fazowego pomiędzy sygnałami X i Y, zaś moduł podniesiony do kwadratu funkcji C to MSC.
Polecenie 1
Zaimplementuj funkcję obliczającą transformatę Fouriera dyskretyzując wzór (9) dla zadanego wektora częstości f i zadanej częstości próbkowania sygnału (tutaj 10.0):
Wywołanie przykładowe:
t= np.arange(0,1,0.1)
x = np.sin(2*np.pi*2*t)
f = np.arange(-5,5,1)
X,f = fourier(x,f,10.0)
print X
Powinno dać:
[ 3.15975012e-16 +5.19678720e-16j 1.05325004e-16 +3.51083347e-16j -4.56408351e-16 -2.10650008e-16j 4.91516686e-16 +1.58113883e+00j -1.40433339e-16 -7.02166694e-17j 0.00000000e+00 +0.00000000e+00j -1.40433339e-16 +7.02166694e-17j 4.91516686e-16 -1.58113883e+00j -4.56408351e-16 +2.10650008e-16j 1.05325004e-16 -3.51083347e-16j]
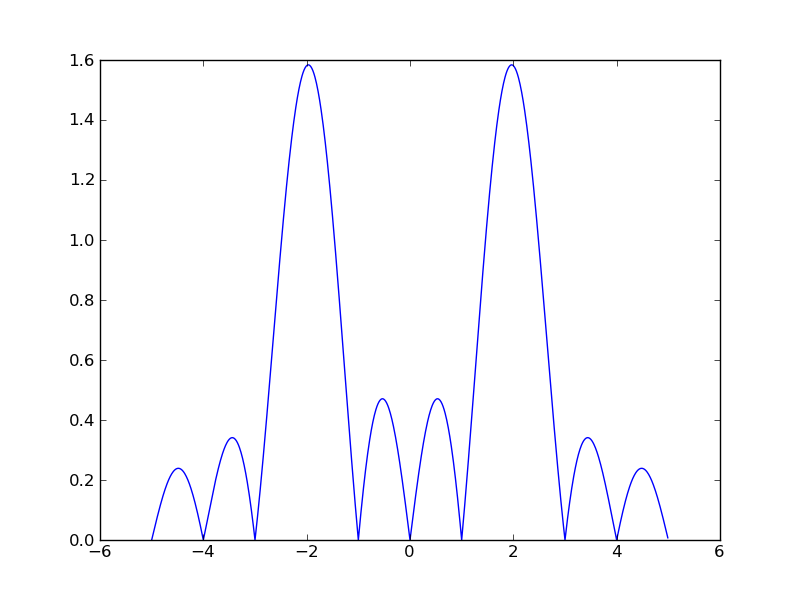
Natomiast wywołanie:
t= np.arange(0,1,0.1)
x = np.sin(2*np.pi*2*t)
f = np.arange(-5,5,0.01)
X = fourier(x,f,10.0)
py.plot(f,np.abs(X))
py.show()
Powinno wytworzyć rysunek:
Polecenie 2
Zaimplementuj funkcję obliczającą koherencję dla pary kanałów. Oblicz i narysuj funkcję koherencji dla kolejnych par kanałów (tych samych co w zadaniu 3). Wyniki zaprezentuj w postaci kwadratowej macierzy rysunków. Ponieważ koherencja jest funkcją zespoloną, dobrze jest zaprezentować osobno jej wartość i fazę. Uzyskane wartości bezwzględne koherencje narysuj nad przekątną tej macierzy, a fazę pod przekątną. W celu obliczenia modułu koherencji i jej fazy wykorzystaj wzór 36 (wygenerowane sygnały należy podzielić na pewną liczbę odcinków)