TI/Matplotlib

Wprowadzenie do pakietu Pylab/Matplotlib na przykładach

Pakiet Pylab/Matplotlib bazuje na pakiecie numerycznym Numpy i korzysta z obiektów w nim zawartych. Pokażemy, jak z jego pomocą rysować różnorodne wykresy prezentujące graficznie przetwarzane dane i wyniki obliczeń. Zamiast wyliczać zawartość pakietu pokażemy ich użyteczność na przykładach. Zaczniemy od prostych i będziemy po drodze omawiać zastosowane w nich konstrukcje.

Wykres funkcji y = f(x)

Prześledźmy działanie poniższego programu:

import pylab
x = [1,2,3]
y = [4,6,5]
pylab.plot(x,y)
pylab.show()

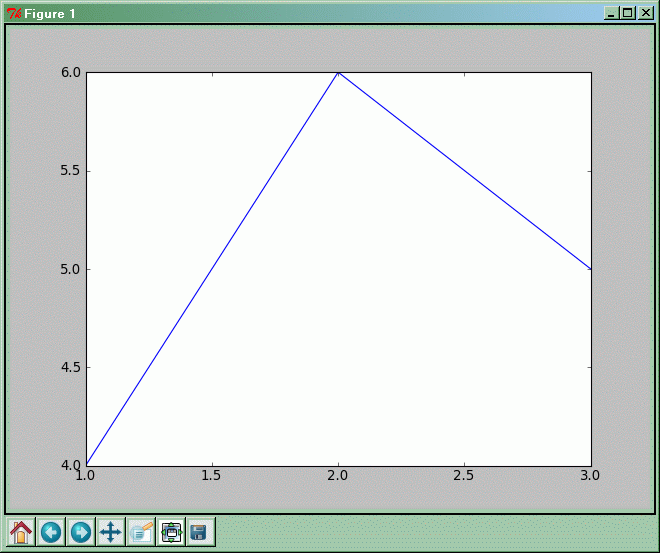
Rezultat

Jak to działa?

Aby skorzystać z pakietu graficznego Pylab importujemy go do naszego programu poleceniem import.

Wytwarzamy dwie listy x i y zawierające ciągi liczb 1, 2, 3 oraz 4, 6, 5.

Funkcja plot rysuje wykres i umieszcza na nim punkty o współrzędnych zawartych w listach przekazanych jej jako argumenty. Pierwszy argument zawiera współrzędne x-owe kolejnych punktów, a drugi argument współrzędne y-owe kolejnych punktów wykresu. Ponieważ listy mają po trzy elementy, tak więc wykres zawierać będzie trzy punkty o współrzędnych (1, 4), (2, 6) oraz (3, 5). Domyślnie punkty na wykresie łączone są ze sobą niebieską linią ciągłą.

Po wywołaniu funkcji plot wykres nie pokazuje się jeszcze na ekranie. Aby go pokazać, używamy funkcji show. Wykres pojawia się na ekranie w osobnym oknie, a Python czeka z wykonywaniem kolejnych instrukcji do momentu zamknięcia okna z wykresem.

W okienku wykresu mamy kilka guzików (po lewej stronie na dole). Służą one do manipulowania wyglądem rysunku. Guzikiem z krzyżykiem możemy zmniejszać/zwiększać skalę na osiach (wciskając prawy guzik myszy i przesuwając kursor po obrazku) oraz przesuwać cały wykres (wciskając lewy guzik myszy i przesuwając kursor po obrazku). Guzik z okienkiem i strzałkami pozwala także zmieniać rozmiar i położenie osi wykresu wewnątrz okna wybierając właściwe wartości. Guzik z domkiem przywraca wyjściowe ustawienia rysunku.

Rysujemy wykres funkcji sinus

import pylab as p
x = p.arange(0.0, 2.0, 0.01)
y = p.sin(2.0*p.pi*x)
p.plot(x,y)
p.show()

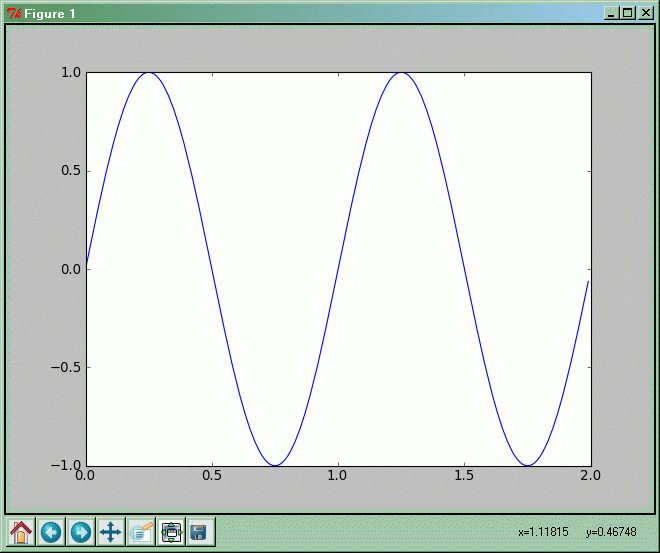
Rezultat

Jak to działa?

Pobieramy do użycia pakiet Pylab pod nazwą p.

Funkcja arange jest podobna do standardowej funkcji range wytwarzającej określone sekwencje liczb w postaci listy. Funkcja arange zamiast listy wytwarza macierz zawierającą ciąg liczb zmiennoprzecinkowych zaczynający się od pierwszego podanego argumentu funkcji arange (u nas 0.0), a kończący się przed drugim argumentem (tradycyjnie, ciąg wynikowy nie zawiera wartości podanej jako drugi argument, u nas 2.0). Różnica między elementami wytworzonego ciągu domyślnie wynosi 1, ale jeśli podamy funkcji arange trzeci argument, to definiuje on nową różnicę ciągu, u nas wynosi on 0.01.

Tak więc zmienna x jest macierzą-wektorem zawierającą ciąg liczb od 0 do 1,99 co 0,01 (czyli 0, 0,01, 0,02, ..., 1,98, 1,99).

Funkcja sin służy do obliczania wartości funkcji sinus dla argumentu podanego w radianach. A co u nas jest argumentem tej funkcji? Wyrażenie będące argumentem zawiera mnożenie liczby 2.0 przez pi (pochodzące z pakietu Pylab), a następnie mnożenie wyniku przez macierz x. Zmienna pi zawiera wartość matematycznej stałej π ≈ 3,1415926. Mnożenie liczby i macierzy, jak wiemy z poprzedniego punktu, daje w wyniku macierz. Oznacza to, że argumentem funkcji sin jest nie liczba, ale macierz! Taka możliwość jest przewidziana przez twórców pakietu Numpy; wynikiem wywołania funkcji jest wtedy również macierz. Jest ona tej samej długości co macierz będąca argumentem wywołania funkcji.

Tak więc zmienna y zawiera ciąg wartości funkcji sinus policzonych dla wartości zawartych w zmiennej x pomnożonych każda przez 2π (czyli sin(2π·0), sin(2π·0,01), sin(2π·0,02), ..., sin(2π·1,98), sin(2π·1,99)).

Funkcja plot(x,y) narysuje zestaw punktów o współrzędnych (0, sin(2π·0)), (0,01, sin(2π·0,01)), (0,02, sin(2π·0,02)), ..., (1,98, sin(2π·1,98)), (1,99, sin(2π·1,99)) połączonych niebieską linią.

Ulepszamy wykres

import pylab as p
x = p.arange(0.0, 2.0, 0.01)
y = p.sin(2.0*p.pi*x)
p.plot(x,y,'r:',linewidth=6)

p.xlabel('Czas')
p.ylabel('Pozycja')
p.title('Nasz pierwszy wykres')
p.grid(True)
p.show()

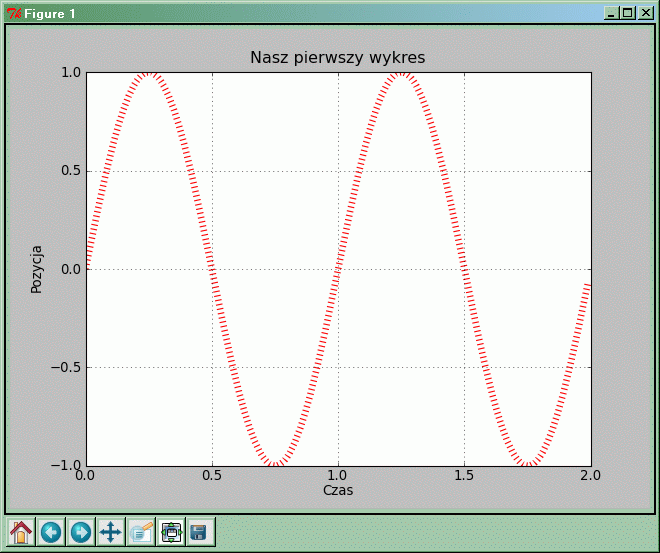
Rezultat

Jak to działa?

W porównaniu z poprzednim przykładem pojawiło się na wykresie kilka drobnych zmian i „ozdobników”.

W funkcji plot pojawiły się dwa nowe parametry:

1. 'r:' — ten parametr steruje wyglądem rysowanej linii wykresu. Pierwsza litera tego napisu określa kolor linii (na przykład r: czerwony, b: niebieski, g: zielony, y: żółty, k: czarny). Drugi znak napisu określa wygląd samej linii (np. -: ciągła, :: kropkowana, o: okrągłe punkty bez linii, +: krzyżyki bez linii, itd.).
2. linewidth=6 — ten parametr zmienia grubość rysowanej linii.

Dodaliśmy też wywołania funkcji xlabel i ylabel. Ich argumentami są napisy, które pojawią się jako opisy osi, odpowiednio poziomej i pionowej. Wywołanie funkcji title wypisuje przekazany jej napis jako tytuł całego wykresu.

Funkcja grid dorysowuje siatkę prostokątną na wykresie w wybranych punktach opisujących wartości na osiach wykresu. Punkty, w których wybierane są wartości opisane na osiach (ang. tick) są wybierane automatycznie (oczywiście jeśli chcemy, możemy zmieniać ich położenie i opisy odpowiednią funkcją, powiemy o tym później).

Kilka wykresów we wspólnych osiach

Pierwsza wersja:

import pylab as p
x = p.arange(0.0, 2.0, 0.01)
y1 = p.sin(2.0*p.pi*x)
y2 = p.cos(2.0*p.pi*x)
p.plot(x,y1,'r:',x,y2,'g')
p.legend(('dane y1','dane y2'))
p.xlabel('Czas')
p.ylabel('Pozycja')
p.title('Wykres ')
p.grid(True)
p.show()

Rezultat:

Jak to działa?

W jednym układzie współrzędnych możemy narysować wiele wykresów. Robimy to podając w jednym poleceniu p.plot kolejno zestawy parametrów opisujące poszczególne linie: współrzędne x, współrzędne y, sposób wykreślania linii. Aby łatwo identyfikować linie można dodać legendę poleceniem legend(). Sposób kontrolowania wyglądu i położenia legendy: help(p.legend) (oczywiście po zaimportowaniu modułu: import pylab as p )

Druga wersja:

import pylab as p
x = p.arange(0.0, 2.0, 0.01)
y1 = p.sin(2.0*p.pi*x)
y2 = p.cos(2.0*p.pi*x)
y = y1*y2
l1, = p.plot(x,y,'b')
l2,l3 = p.plot(x,y1,'r:',x,y2,'g')
p.legend((l2,l3,l1),('dane y1','dane y2','y1*y2'))
p.xlabel('Czas')
p.ylabel('Pozycja')
p.title('Wykres ')
p.grid(True)
p.show()

Rezultat:

Jak to działa?

Wykresy możemy dodawać do współrzędnych kolejnymi poleceniami p.plot. Funkcja p.plot zwraca listę linii. Notacja l1, = p.plot(x,y,'b') wydobywa z listy pierwszą linię (Gdyby po l1 nie było przecinka to l1 byłoby listą zawierającą jeden obiekt klasy linia ).

Dzięki nazwaniu poszczególnych obiektów linii możemy kontrolować ich kolejność (i obecność) na legendzie.

Histogram (diagram liczebności)

import pylab as p

zliczenia = p.array([0, 1, 2, 2, 3, 3, 3, 3, 3, 3, 4, 4, 4, 5, 7])

p.hist(zliczenia)
p.show()

Rezultat:

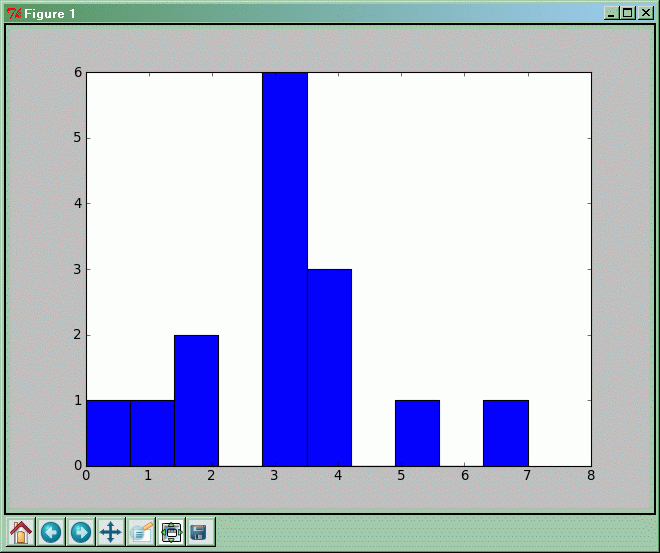
Jak to działa ?

Do zmiennej zliczenia przypisujemy macierz z ręcznie podanymi wartościami. Zakres zmienności badanych zliczeń (odkładany na osi X) dzielimy na przedziały (ang. bin) o jednakowej „szerokości”; domyślnie będzie ich 10. Funkcja p.hist() zlicza wystąpienia wartości w binach i rysuje histogram. Funkcja ta zwraca krotkę (array ze zliczeniami, array z binami, lista zawierająca prostokąty, które histogram rysuje, tzw. obiekty Patch).
Pełna lista parametrów tej funkcji jest następująca:

      hist(x, bins=10, range=None, normed=False, cumulative=False,
          bottom=None, histtype='bar', align='mid',
          orientation='vertical', rwidth=None, log=False, **kwargs)

Poniżej opisujemy znaczenie najistotniejszych parametrów.

• Możemy kontrolować albo ilość binów jeśli bins jest liczbą, albo położenie binów (może być nierównomierne) jeśli bins jest sekwencją.
• range kontroluje zakres przeliczanych danych. Domyślnie jest to (x.min(), x.max()). Jeśli podamy inne wartości to dane mniejsze od dolnego zakresu i większe od górnego zakresu nie zostaną uwzględnione.
• normed kontroluje czy zliczenia w binach mają być unormowane do jedności — może to być przydatne do wykreślania np. rozkładów gęstości prawdopodobieństwa.
• Jeżeli parametr cumulative ma wartość True to kolejne biny mają do swojej własnej ilości zliczeń dodawaną sumę zliczeń wszystkich dotychczasowych (dla mniejszych wartości x) binów. W ten sposób możemy na przykład narysować dystrybuantę rozkładu prawdopodobieństwa.

Pozostałe argumenty kontrolują wygląd i układ rysunku. Ich znaczenie można poznać z dokumentacji help(p.hist)

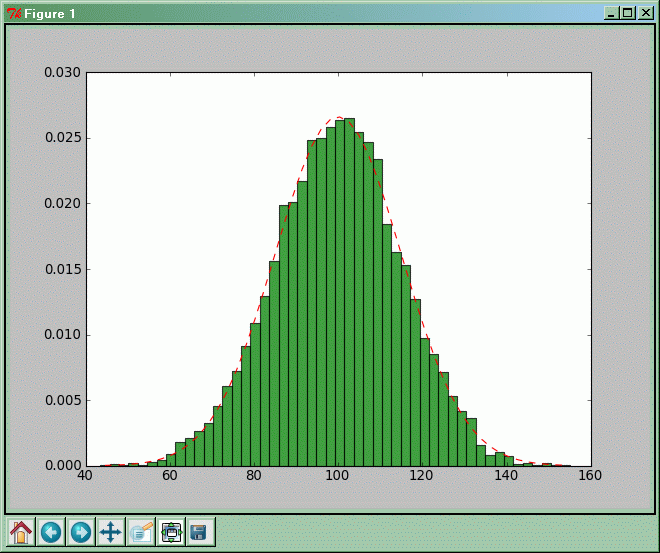
Bardziej zaawansowany przykład:

Wyjaśnienie działania znajduje się w komentarzach do programu:

import pylab as p
import numpy 

mi, sigma = 100, 15
x = mi + sigma * numpy.random.randn(10000)
# numpy.random.randn zwraca array z liczbami pseudolosowymi
# pochodzącymi z rozkładu normalnego o średniej 0 i wariancji 1
# przemnożenie przez odchylenie standandardowe sigma i dodanie śreniej mi
# transformuje rozkład do rozkładu normalnego o średniej mi i wariancji sigma**2


n, bins, patches = p.hist(x, 50, normed=True, facecolor='green', alpha=0.75)
# Tu w jawny sposób odbieramy zwracane przez p.hist obiekty
# Zmieniamy też:
#   - ilość binów na 50
#   - normujemy histogram do jedności
#   - ustalamy kolor prostokątów na zielony
#   - ustawiamy przezroczystość prostokątów na 0.75

bincenters = 0.5*(bins[1:]+bins[:-1])
# wytwarzamy array z centrami binów korzystając z granic binów
# zwróconych przez p.hist w macierzy bins

y = p.normpdf( bincenters, mi, sigma)
# obliczamy wartości w normalnym rozkładzie gęstości prawdopodobieństwa
# o średniej mi i wariancji sigma**2 dla wartości bincenters

l = p.plot(bincenters, y, 'r--', linewidth=1)
# do histogramu dorysowujemy linię 

p.show()

Rezultat:

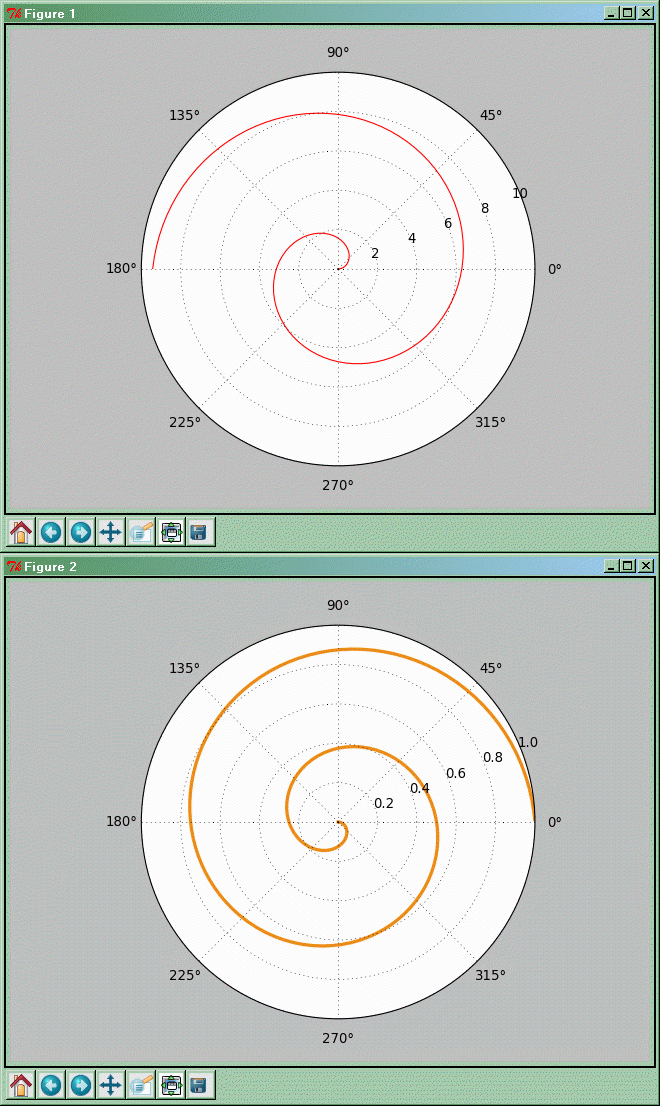
Wykres biegunowy

import pylab as p

p.figure()
teta = p.arange(0,3*p.pi,0.001)
r = teta
p.polar(teta, r, color='red')

p.figure()
r = p.arange(0,1,0.001)
teta = -2*2*p.pi*r
p.polar(teta, r, color='#ee8d18', lw=3)

p.show()

Rezultat:

Zadanie: Wykresy funkcji w układzie biegunowym

Dotychczasowe wykresy wykonywane funkcją plot rysowane były w kartezjańskim układzie współrzędnych, gdzie podawaliśmy położenie punktów (x, y) jako ich odległości od środka układu w kierunku poziomym i pionowym. W układzie biegunowym położenie punktów podajemy w postaci (r, θ), które opisują odległość od środka układu i kąt (prostej łączącej punkt i środek układu) z osią poziomą.

Narysuj wykresy krzywych, które zdefiniowane są w układzie biegunowym następującymi zależnościami:

1. Okrąg [math]r( \theta ) =a[/math].
2. Spirala Archimedesa [math]r(\theta)=a\theta[/math].
3. Spirala hiperboliczna [math]r(\theta)=a/\theta[/math].
4. Elipsa [math]r(\theta)=\frac{1+\varepsilon}{1+\varepsilon\cos\theta}[/math], dla 0 < ε < 1.
5. Trifolium [math]r(\theta)=a\cos\theta(4\sin^2\theta-1)[/math].

Prosta animacja

import pylab as p
p.ion()
a=1.0
teta = p.arange(0,2*p.pi,0.1)
r = a*p.cos(3*teta)
linia, = p.polar(teta, r, color='red')
for fi in p.arange(0,p.pi,0.01):
    r = a*p.cos(3*teta+fi)
    linia.set_ydata(r)
    p.draw()

Jak to działa

Uwaga: ta metoda animowania nie działa w Windows.

Pod linuksem ten typ animacji działa i można go zrozumieć w następujący sposób. Funkcja p.ion() przełącza system graficzny w tryb interaktywny. Wywołanie funkcji p.polar wytwarza obiekt linia dany równaniem [math]r(\theta)=a \cos(3 \theta)[/math]. Następnie w każdej iteracji pętli obliczamy nowy zestaw punktów definiujących linię dla aktualnej wartości fi, zgodnie z równaniem [math]r(\theta)=a \cos(3 \theta + \phi)[/math]. Wyliczone wartości r podstawiamy do obiektu linia. Funkcja p.draw() powoduje wyczyszczenie poprzedniej wersji rysunku i odrysowanie aktualnej reprezentacji obiektu linia.

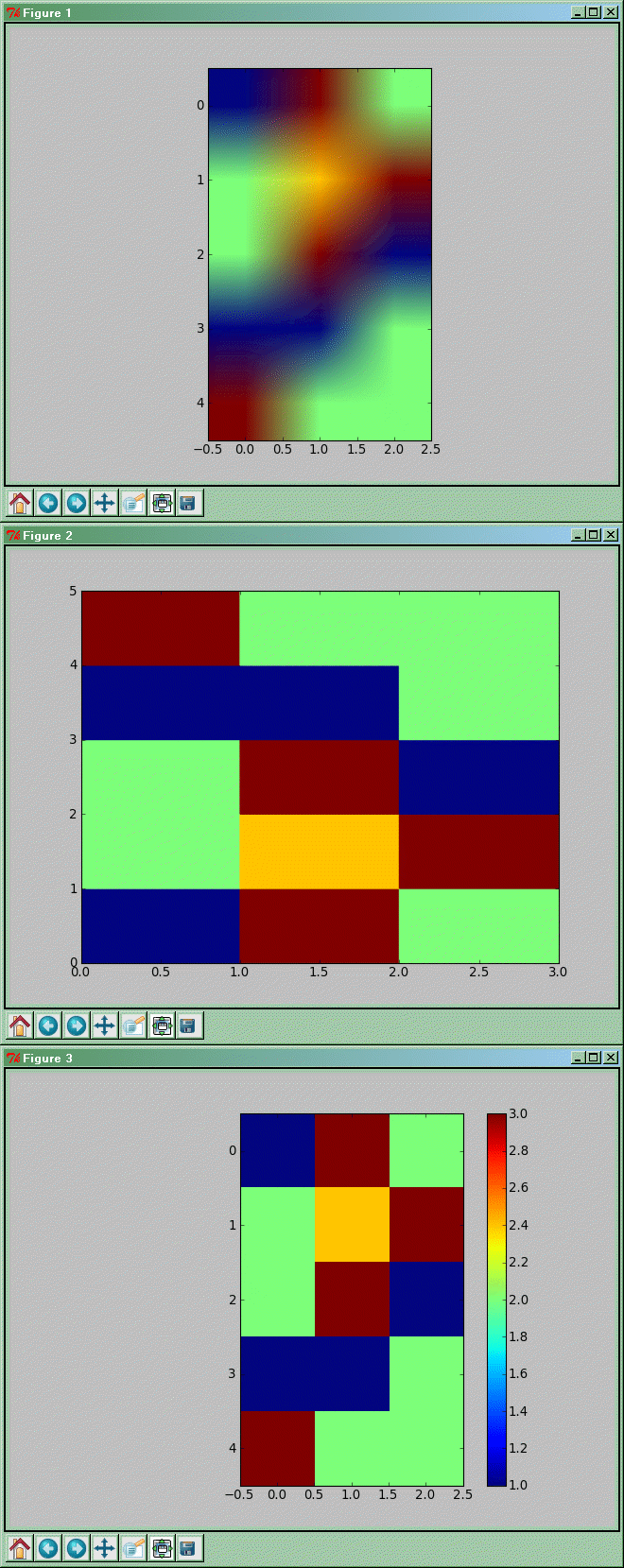
Wizualizacja zawartości macierzy dwuwymiarowej

import pylab as p

X = p.array([[1,  3,   2],
             [2,  2.4, 3],
             [2,  3,   1],
             [1,  1,   2],
             [3,  2,   2]])

p.figure()
p.imshow(X)

p.figure()
p.pcolor(X)

p.figure()
p.imshow(X, interpolation='nearest')
p.colorbar()

p.show()

Rezultat:

Powierzchnia dwuwymiarowa w przestrzeni trójwymiarowej

Do rysowania prostych wykresów w przestrzeni trójwymiarowej można użyć dodatku do modułu matplotlib mpl_toolkits.mplot3d. Poniższy przykład demonstruje jego użycie.

from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
import pylab as p
import numpy as np

fig = p.figure() # wytwarzamy obiekt typu figura 
ax = Axes3D(fig) # wytwarzamy obiekt osie 3D
X = np.arange(-15, 15, 0.3) # wektor opisujący oś X
Y = np.arange(-15, 15, 0.3) # wektor opisujący oś Y
X, Y = np.meshgrid(X, Y)    # zamieniamy wektory osi w siatkę, której węzły są 
#zadane przez odpowiadające sobie elementy w macierzach X i Y      
# dla każdego węzła obliczamy jego odległość od początku układu współrzędnych               
R = np.sqrt(X**2 + Y**2)
# dla każdego węzła obliczamy wartość funkcji Z
Z = np.sin(R)/R
# generujemy rysunek powierzchni  
# parametry <tt>rstride=2, cstride=2</tt> służą do próbkowania siatki (tu bierzemy co drugi węzeł),
# parametr <tt>cmap=cm.jet</tt> definiuje jaką mapę kolorów zastosować
ax.plot_surface(X, Y, Z, rstride=2, cstride=2,cmap=cm.jet)
# pokazujemy gotowy rysunek
p.show()

Rezultat:

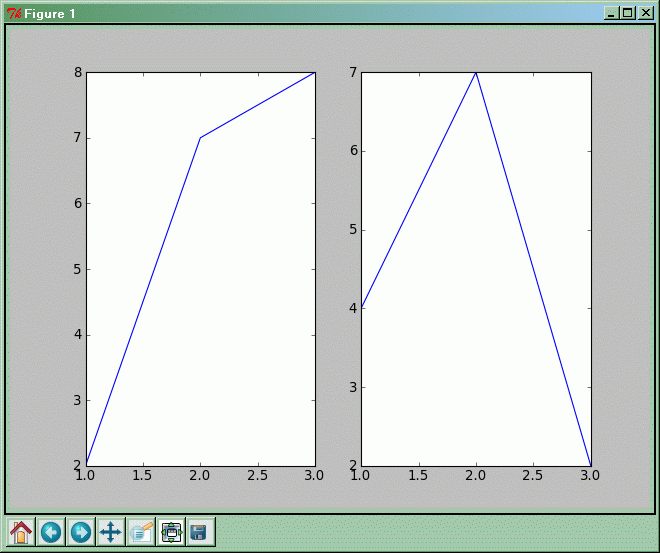
Wiele wykresów w jednym oknie

import pylab as p

p.subplot(1,2,1)
p.plot([1,2,3],[2,7,8])

p.subplot(1,2,2)
p.plot([1,2,3],[4,7,2])

p.show()

Rezultat:

Przykład: Ruch jednostajnie przyspieszony

import pylab as p
''' Ruch jednostajnie przyspieszony:
demonstracja subplotów i całkowania metodą Eulera'''
dt=0.1 # definiujemy krok czasu
       # -- mniejszy krok czasu większa dokładność całkowania
t=p.arange(0,10,dt) # wytwarzamy oś czasu
# definiujemy parametry początkowe dla rozważanego ruchu
x0=1        
v0=0.5
a0=0.5
# analityczne całkowanie ruchu ze stałym przyspieszeniem
# daje następujące wyrażenia:

a=a0*p.ones(len(t),)        # przyspieszenie
v=v0 + a*t                  # prędkość
x=x0 + v0*t + a*t**2/2.0    # położenie
# rysujemy wykresy
# przyspieszenia, prędkości i położenia od czasu
# uzyskane przez całkowanie analityczne
p.subplot(3,1,1)
p.plot(t,a)
p.subplot(3,1,2)
p.plot(t,v)
p.subplot(3,1,3)
p.plot(t,x)


# obliczamy numerycznie wartości prędkości w kolejnych chwilach czasu
v_num = p.zeros(len(t),)
v_num[0]=v0
for i in range(1,len(t)):
    v_num[i]=v_num[i-1]+a0*dt
# obliczamy numerycznie wartości położenia w kolejnych chwilach czasu
x_num = p.zeros(len(t),)
x_num[0]=x0
for i in range(1,len(t)):
    x_num[i]=x_num[i-1]+v_num[i-1]*dt

# do wykresów uzyskanych analitycznie dorysowujemy wyniki numeryczne
p.subplot(3,1,2)
p.plot(t,v_num,'r')
p.subplot(3,1,3)
p.plot(t,x_num,'r') 
p.show()

Rezultat:

Zadanie: Figury Lissajous

Proszę zrobić program wykreślający krzywą [math]y(x)[/math], gdzie [math]x=A \sin(\omega_a t + \phi_a)[/math] zaś [math]y=B \sin(\omega_b t + \phi_b)[/math].

http://pl.wikipedia.org/wiki/Krzywa_Lissajous