Chemia/Budowa atomu

Atom i pierwiastek — podstawowe definicje

Atom jest najmniejszą częścią pierwiastka zachowującą jego właściwości. Zbudowany jest z jądra atomowego oraz elektronów. W skład jądra wchodzą protony i neutrony (nukleony). Podstawowe właściwości tych cząstek elementarnych zebrano w tabeli.

Cząstka	Symbol	Zapis	Masa [kg]	Ładunek [e]	Ładunek [C]
proton	p	[math]_1^1p[/math]	[math]1,6726231 \cdot 10^{-27}[/math]	1	[math]1,602 \cdot 10^{-19}[/math]
neutron	n	[math]_1^0n[/math]	[math]1,6749286 \cdot 10-27[/math]	0	0
elektron	e	[math]_0^{-1}e[/math]	[math]9,1093897 \cdot 10^{-31}[/math]	-1	[math]1,602 \cdot 10^{-19}[/math]

Atom przedstawia się za pomocą symbolu odpowiedniego pierwiastka oraz liczby masowej i atomowej:

A — liczba masowa (liczba nukleonów)

[math]_\mathrm{A}^\mathrm{E} Z [/math] — symbol pierwiastka

Z — liczba atomowa (liczba protonów)

Pierwiastek chemiczny jest zbiorem atomów o takiej samej liczbie protonów, a nuklid zbiorem atomów o tej samej liczbie atomowej i masowej.

• Izotopy — atomy tego samego pierwiastka różniące się liczbą masową
• Izobary — zbiory atomów o takiej samej liczbie masowej
• Izotony — zbiory atomów o takiej samej liczbie neutronów

Odmiany alotropowe — odmiany tego samego pierwiastka różniące się liczbą atomów w cząsteczce (tlen i ozon) lub postacią krystaliczną (diament i grafit).

Modele atomu

Model atomu Rutherforda	Model atomu Bohra	Model atomu Schrödingera

Modele zaproponowane przez Rutherforda i Bohra były oparte na prawach fizyki klasycznej Newtona. Mechanika klasyczna pozwala dokładnie określić położenie i pęd obiektów materialnych w każdym punkcie czasowym oraz przewiduje możliwość wzbudzenia ruchów translacyjnych, rotacyjnych i oscylacyjnych do dowolnych wartości energii pod wpływem przyłożenia siły.

Model planetarny Rutherforda (1911)

W centralnej części atomu znajduje się dodatnio naładowane jądro, dookoła którego krążą elektrony po torach kołowych lub eliptycznych.

Model Bohra (1913)

Elektron w atomie może przebywać w ściśle określonych stanach o określonej energii. Podczas przejścia elektronu ze stanu o wyższej energii (E₂) do stanu o niższej energii (E₁) następuje emisja energii, natomiast przejście ze stanu (_E1) do stanu (E₂) wymaga absorpcji energii

E₂ - E₁ = hν

Teoria Bohra wyjaśniała emisje fal świetlnych pozwalającą wytłumaczyć widmo emisyjne atomu wodoru oraz atomów wodoropodobnych (brak możliwości opisu pozostałych atomów).

Przełomowe doświadczenia w badaniach nad strukturą atomów

• Elektryczne wyładowania w gazach
• Spektroskopia atomowa
• Efekt fotoelektryczny

Widmo atomu wodoru

Linie spektralne tworz grupy o zbliżonych długościach fal, zwane seriami (Lymana, Balmera, Paschena).

Spektrum widzialne atomu wodoru (seria Balmera).Występowanie dyskretnych linii spektralnych wskazuje, że elektron w atomie może przyjmowad pewne określone energie.

Efekt fotoelektryczny

Wyładowania elektryczne w gazowym wodorze. Strumień elektronów rozszczepia cząsteczki wodoru i wzbudza powstające atomy do wyższych stanów energetycznych. Oddając nadmiar energii atomy emitują promieniowanie, które przechodząc przez pryzmat ulega załamaniu i na ekranie powstaje widmo liniowe gazu.

Model prostego spektroskopu złożonego z kartonu ze szczeliną i pryzmatu.

Falowa natura elektronu

• Louis de Broglie (1924) przypisał elektronom właściwości korpuskularne oraz falowe (dualizm korpuskularno-falowy) wyrażone wzorem
  

  [math]\lambda=\frac h {mv}[/math]
  

  gdzie m oznacza masę cząstki, v — prędkość , h — stałą Plancka.
• Doświadczalne potwierdzenie dualizmu elektronu nastąpiło w roku 1927, kiedy odkryto zjawisko dyfrakcji elektronów (C.J. Davisson, L.H. Germer).
• W przypadku cząstek elementarnych niemożliwe jest równoczesne dokładne określenie położenia i pędu (zasada nieoznaczoności Heisenberga).
  Zasada nieoznaczoności wyrażana jest w postaci
  

  [math]\Delta x\Delta p_x \geq \frac{h}{4\pi}[/math]
  

  gdzie [math]\Delta x[/math] jest miarą niedokładności oznaczenia współrzędnej określającej położenie cząstki, a [math]\Delta p_x[/math] miarą niedokładności oznaczenia pędu cząstki.

Równanie Schrödingera

Równanie Schrödingera opisuje ruch cząstek. Funkcja będąca jego rozwiązaniem, nazywana funkcją falową ([math]\Psi[/math]), opisuje stan pojedynczej cząstki lub wielu cząstek.

[math]\frac{\partial^2 \Psi}{\partial x^2}+\frac{\partial^2 \Psi}{\partial y^2}+ \frac{\partial^2 \Psi}{\partial z^2} +\frac{8\pi m}{h^2}\left(E\Psi-V\Psi\right)=0[/math]

Kwadrat bezwzględnej wartości funkcji [math]\Psi[/math] jest miarą gęstości elektronowej w różnych obszarach wokół jądra

[math]\rho(x,y,z) = |\Psi(x,y,z)|^2\;[/math]

Dla atomu wodoru funkcje falowe można dokładnie wyznaczyć, jednak tylko niektóre z nich, tzw. funkcje porządne (ciągłe, jednoznaczne i przyjmujące wartości skończone), nadają się do wyrażenia prawdopodobieństwa napotkania elektronu.

Co wynika z postulatów mechaniki kwantowej?

• Nie da się określić toru elektronu, lecz jedynie prawdopodobieństwo jego znalezienia w wybranym rejonie przestrzeni wokół jądrowej. Przyjmuje się, że elektron wytwarza chmurę ładunku ujemnego wokół jądra a kształt chmury zależy od stanu kwantowego.
• Ruch elektronu jest opisywany za pomocą równania Schrödingera, którego rozwiązaniem są funkcje falowe. Znajomość tych funkcji pozwala na obliczanie różnych wielkości związanych z ruchem elektronu.
• W zależności od wartości parametrów charakteryzujących stan elektronu wprowadzono umowną, trójstopniową klasyfikację stanów kwantowych: powłoki, podpowłoki, poziomy orbitalne.

Cechy mikroświata

Wielkości fizyczne związane z ruchem cząstki nie mogą przyjmować wartości dowolnych — są to wielkości skwantowane.

W przypadku elektronu kwantowaniu podlega 5 parametrów ruchu:

• energia,
• orbitalny moment pędu,
• orientacja przestrzenna orbitalnego momentu pędu,
• spin,
• orientacja przestrzenna spinu.

Stan elektronu określony za pomocą wartości poszczególnych parametrów jest nazywany stanem kwantowym.

Energia atomu wodoru

Rozwiązaniem równania Schrödingera mogą być funkcje porządne tylko wtedy, gdy energia elektronu w atomie o liczbie atomowej Z wyraża się równaniem

[math]E= -\frac{m_ee^4Z^2}{8\varepsilon_0^2h^2n^2}[/math]

gdzie n - główna liczba kwantowa, która może przybierać wartości kolejnych liczb naturalnych, e - ładunek elementarny, [math]m_e[/math] — masa elektronu, [math]\varepsilon_0[/math] — przenikalność elektryczna próżni, h — stała Plancka.

Energia elektronu w atomie wodoru może przyjmować następujące wartości:

• E₁ =-13,59 eV dla n = 1
• E₂ =-3,44 eV dla n = 2
• E₃ =-1,56 eV dla n = 3

Ujemne wartości energii wynikają z założenia, że energia potencjalna elektronu znajdującego się w nieskończenie dużej odległości od jądra ma wartość zerową, zatem w miarę zbliżania się elektronu do jądra przyjmuje wartości coraz bardziej ujemne.

Stany kwantowe o takiej samej energii nazywa się stanami zdegenerowanymi. W atomie wodoru liczba stanów zdegenerowanych wynosi [math]2n^2[/math].

Wartość energii (-13,6 eV) wynikającą z warunku kwantowego [math]n = 1[/math] posiadają dwa stany kwantowe. Kolejna wartość energii (-3,4 eV) uzyskana dla [math]n = 2[/math], odpowiada 8 stanom kwantowym.

Zbiór stanów kwantowych o tej samej wartości n (głównej liczby kwantowej) jest nazywany powłoką elektronową (zarówno w atomie wodoru, jak i w atomach wieloelektronowych).

Główna liczba kwantowa n spełnia następujące funkcje:

• określa liczbę stanów kwantowych w powłoce jako równą [math]2n^2[/math],
• kwantuje energię.

Powłoki elektronowe w atomie (wartości energii dotyczą atomu wodoru):

• [math]n = 1[/math] powłoka K zawierająca 2 stany o energii -13,6 eV
• [math]n = 2[/math] powłoka L zawierająca 8 stanów o energii -3,4 eV
• [math]n = 3[/math] powłoka M zawierająca 18 stanów o energii -1,5 eV
• [math]n = 4[/math] powłoka N zawierająca 32 stany o energii -0,85 eV
• [math]n = 5[/math] powłoka Q zawierająca 50 stanów o energii -0,54 eV

Kwantowanie momentu pędu i spinu

• Ruch elektronu opisywany jest wielkością wektorową zwaną orbitalnym momentem pędu, co powoduje konieczność oddzielnego kwantowania jego wartości i orientacji przestrzennej .
• Wartość momentu pędu kwantuje poboczna (orbitalna) liczba kwantowa [math]\ell[/math], która może przybierać wartości od 0 do [math]n -1[/math].
• Zbiór stanów kwantowych o tej samej energii i tej samej wartości momentu pędu (czyli zbiór stanów opisywanych tym samym zestawem liczb [math]n[/math] i [math]\ell[/math]), jest nazywany podpowłoką elektronową.
• Każda powłoka elektronowa zawiera inną liczbę podpowłok, równą [math]n[/math], które oznacza się symbolami: [math]s[/math] (dla [math]l = 0[/math]), [math]p[/math] (dla [math]l = 1[/math]), [math]d[/math] (dla [math]l = 2[/math]), [math]f[/math] (dla [math]l = 3[/math]), a dalej alfabetycznie.
• Wektor momentu pędu może przyjmować [math]2l + 1[/math] ustawień względem zewnętrznego pola magnetycznego.
• Kwantowanie orientacji przestrzennej wektora momentu pędu polega na znalezieniu rzutów tego wektora na kierunek zewnętrznego pola magnetycznego. Określa je magnetyczna liczba kwantowa [math](m)[/math] przybierająca wartości liczb całkowitych od –l do +l. Zbiór stanów kwantowych o jednakowych wartościach liczb [math]n,\ l,\ m[/math] nazywa się poziomem orbitalnym.
• Wielkość zwaną spinem przypisano ruchowi wewnętrznemu elektronu, odpowiedzialnemu za wytworzenie pola magnetycznego wokół elektronu. Wartość spinu określa spinowa liczba kwantowa [math](s)[/math], która przyjmuje tylko jedną wartość (½), natomiast wektor spinu może ustawić się względem zewnętrznego pola magnetycznego na dwa sposoby: „spin równoległy” i „spin antyrównoległy”.
• Kwantowanie orientacji przestrzennej spinu wprowadza magnetyczną spinową liczbę kwantową ([math]m_s[/math]), która może przyjmować dwie wartości (+ ½) i (- ½).
• Poziom orbitalny to 2 stany kwantowe opisane tymi samymi liczbami kwantowymi [math](n,\ l,\ m)[/math], a różniące się orientacją przestrzenną wektora spinu w zewnętrznym polu magnetycznym.

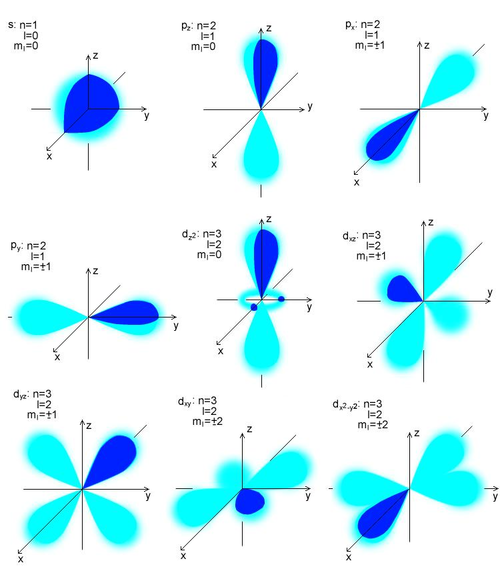
Orbitale atomowe wodoru

• Każdej kombinacji 3 liczb kwantowych [math](n,\ l,\ m)[/math] odpowiada jedna funkcja falowa spełniająca równanie Schrödingera.
• Funkcja taka nazywa się orbitalem atomowym [math]\left(\Psi_{n,l,m}\right)[/math]. Liczbę możliwych orbitali odpowiadających poszczególnym wartościom głównej liczby kwantowej (poszczególnym dozwolonym stanom energetycznym atomu wodoru) określa się na podstawie różnych możliwych kombinacji liczb kwantowych.
• Znajomość postaci funkcji stanowiących orbitale atomowe pozwala obliczyć prawdopodobieństwo napotkania elektronu w określonych odległościach od jądra i w określonych kierunkach.

Kształty orbitali s, p, d

Orbitale w atomach wieloelektronowych

• Dla atomów wieloelektronowych równanie falowe ma tak skomplikowaną postać, że nie można go rozwiązać w sposób ścisły (problemem jest konieczność uwzględnienia współrzędnych wszystkich elektronów oraz oddziaływań pomiędzy nimi).
• Możliwe jest uzyskanie rozwiązań przybliżonych za pomocą metody pola samouzgodnionego (Hartree-Focka), w której rozpatruje się ruch poszczególnych elektronów w uśrednionym polu elektrycznym innych elektronów. Pozwala to na opisanie każdego elektronu oddzielną funkcją falową, uwzględniającą tylko współrzędne opisywanego elektronu. Działanie takie nazywa się przybliżeniem jednoelektronowym, a funkcja falowa opisująca zachowanie się wszystkich elektronów jest iloczynem orbitali jednoelektronowych
• Istotna różnica pomiędzy atomem wodoru a atomami wieloelektronowymi polega na tym, że o energii elektronu w atomie wodoru decyduje wyłącznie główna liczba kwantowa, podczas gdy w pozostałych atomach na energie elektronów wpływa również orbitalna liczba kwantowa.

Zapełnianie powłok elektronowych

• W atomie wieloelektronowym nie może być dwóch elektronów, których stan jest opisywany za pomocą zestawów identycznych liczb kwantowych, muszą się różnić przynajmniej jedną liczbą kwantową.
• Zgodnie z zakazem Pauliego, jeden orbital o liczbach kwantowych n,l,m może opisywać zachowanie się co najwyżej dwóch elektronów różniących się spinową liczbą kwantową.
• Z punktu widzenia właściwości chemicznych znaczenie mają elektrony tworzące najbardziej zewnętrzną powłokę elektronową, tzw. elektrony walencyjne.
• Przyporządkowując elektrony orbitalom zdegenerowanym (o jednakowych energiach), należy je rozmieszczać pojedynczo ze zgodnie skierowanymi spinami, ponieważ zgodnie z regułą Hunda najniższą energię dla danej konfiguracji ma stan o najwyższym możliwym całkowitym spinie.
• Stan, w którym pojawiają się niesparowane elektrony (ze zgodnie skierowanymi spinami) nazywa się stanem trypletowym. Stan, w którym atom nie zawiera żadnego elektronu niesparowanego, nazywa się stanem singletowym.
• W miarę przechodzenia do atomów o coraz większej liczbie atomowej poziomy energetyczne są zajmowane w kolejności, według której wzrasta ich energia.

Konfiguracje elektronowe pierwiastków

• Konfiguracją elektronową pierwiastka określa się rozmieszczenie elektronów w podpowłokach i powłokach
• Kolejność zapełniania podpowłok elektronami określa reguła [math]n+ l[/math]:
  

  elektrony zajmują w pierwszej kolejności tę podpowłokę, dla której suma [math](n+l)[/math] jest najmniejsza; gdy dwie podpowłoki mają jednakową sumę [math](n+l)[/math] to o kolejności zapełniania decyduje mniejsza wartość [math]n[/math]:
  

  [math]1s^22s^22p^63s^23p^64s^23d^{10}4p^{6}5s^24d^{10}5p^{6}6s^{2}4f^{14}5d^{10}6p^67s^2[/math]
  

  Przykładowe konfiguracje:
  

  ¹²Mg [math]1s^2 2s^22p^6 3s^2[/math] lub w formie skróconej [Ne][math]3s^2[/math]
  

  ²⁵Mn [math]1s^22s^22p^6 3s^23p^6 4s^23d^5[/math] lub w formie skróconej [Ar][math]4s^23d^5[/math]