WnioskowanieStatystyczne/Regresja liniowa
Wnioskowanie_Statystyczne_-_wykład
Regresja liniowa
Pary pomiarów [math](x_{i},y_{i})[/math]. Dla każdego [math]x_{i}[/math], [math]y_{i}[/math] traktujemy jak zmienną losową z rozkładu normalnego o wartości średniej [math]a+b[/math] [math]x_{i}[/math] i wariancji [math]\sigma _{i}^{2}[/math]. Prawdopodobieństwo a posteriori otrzymania [math]N[/math] wyników [math]y_{i}[/math] dla określonych [math]x_{i}[/math] przy założeniu wartości [math]a[/math] i [math]b[/math]
[math] P(\overline{y}\mid \overline{x},a,b) =\underset{i=1}{\overset{N}{\prod }} \frac{1}{\sqrt{2\pi \sigma _{i}^{2}}}e^{\frac{(y_{i}-a-bx_{i})^{2}}{2\sigma_{i}^{2}}} =\frac{1}{\sqrt{(2\pi )^{n}}} \cdot \underset{i=1}{\overset{N}{\prod }} \frac{1}{\sigma _{i}} \cdot e^{-\frac{1}{2}\underset{i=1}{\overset{N}{\sum }}\frac{ (y_{i}-a-bx_{i})^{2}}{\sigma _{i}^{2}}} [/math]
logarytmiczna funkcja wiarygodności:
[math] l=-\frac{N}{2}\ln 2\pi +\ln (\underset{i=1}{\overset{N}{\prod }}\frac{1}{ \sigma _{i}})-\frac{1}{2}\underset{i=1}{\overset{N}{\sum }}\frac{ (y_{i}-a-bx_{i})^{2}}{\sigma _{i}^{2}} [/math]
[math]\sigma _{i}[/math] zwykle nie znamy, możemy przyjąć [math]\forall i \sigma _{i}=\sigma[/math]. Pozostaje szukanie minimum sumy [math]S=\underset{i=1}{\overset{N}{\sum }}(y_{i}-a-bx_{i})^{2}[/math], w zerze pochodnej po parametrach [math]a[/math] i [math]b[/math]
[math] \frac{\partial S}{\partial a}=-2\underset{i=1}{\overset{N}{\sum }}(y_{i}-a-bx_{i})\\ \sum_{i=1}^N \left(y_i - a - bx_i\right) = 0 \\ \sum_{i=1}^N y_i = \sum_{i=1}^N a + b\sum_{i=1}^N x_i \\ \sum_{i=1}^N y_i = n a + b\sum_{i=1}^N x_i \\ \frac{1}{N}\sum_{i=1}^N y_{i} = a + \frac{1}{N} b\sum_{i=1}^N x_i [/math]
[math] \bar{y} = a + b\bar{x} [/math]
[math] a = \bar{y} - b\bar{x} [/math]
wyznaczone stąd [math]a[/math] podstawiamy do wzoru na [math]S[/math]
[math] S=\underset{i=1}{\overset{N}{\sum }}(y_{i}-a-bx_{i})^{2} [/math]
[math] = \underset{i=1}{\overset{N}{\sum }}(y_{i}-\bar{y} - b\bar{x}-bx_{i})^{2} [/math]
[math] =\underset{i=1}{\overset{N}{\sum}} \left( (y_{i}-\bar{y}) - b (x_i - \bar{x}) \right)^2 [/math]
po podstawieniu liczymy pochodną po [math]b[/math]
[math] \frac{\partial S}{\partial b}= -2\sum_{i=1}^N \left[\left(y_{i} - \bar{y}\right) - b\left(x_{i} - \bar{x}\right)\right]\left(x_{i}-\bar{x}\right) = 0 [/math] [math] \sum_{i=1}^N \left(y_{i} - \bar{y}\right)\left(x_i - \bar{x}\right) - b\sum_{i=1}^N \left(x_i - \bar{x}\right)^2 = 0 [/math] [math] b = \frac{\sum_{i=1}^N \left(y_{i} - \bar{y}\right)\left(x_i - \bar{x}\right)}{\sum_{i=1}^N \left(x_{i}-\bar{x}\right)^2} [/math]
czyli
[math] b=\frac{\underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x})(y_{i}- \overline{y})}{\underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x})^{2}}, \qquad a=\overline{y}-b\overline{x} [/math]
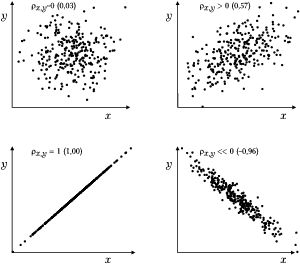
Interpretacja współczynnika korelacji
Rozważmy wariancję zmiennej [math]y[/math] z poprzedniego rozdziału. Niech [math]y_{i}^{p}=a+bx_{i}[/math]
[math] \underset{i=1}{\overset{N}{\sum }}(y_{i}-\overline{y})^{2}= \underset{i=1}{\overset{N}{\sum }}(y_{i}-y_{i}^{p}+y_{i}^{p}-\overline{y} )^{2}= [/math] [math] \underset{i=1}{\overset{N}{\sum }}(y_{i}-y_{i}^{p})^{2}+\underset{i=1}{ \overset{N}{\sum }}(y_{i}^{p}-\overline{y})^{2}+2\underset{i=1}{\overset{N}{ \sum }}(y_{i}-y_{i}^{p})(y_{i}^{p}-\overline{y}) [/math]
Całkowitą wariancię zmiennej [math]y[/math] podzieliliśmy na dwa człony: wariancję estymaty [math]y_{i}^{p}[/math] wokół wartości średniej [math]\overline{y}[/math] i wariancję obserwowanych [math]y_{i}[/math] wokół estymaty [math]y_{i}^{p}[/math] (trzeci człon znika).
Współczynnik korelacji
[math]
\rho_{x, y}= \frac{\sigma_{x, y}}{\sigma_x \sigma_y}=
\frac{E\left( \left(x-\mu_{x})(y-\mu_{y}\right)\right)}
{\sqrt{E\left( (x-\mu_{x})^2\right) E\left( (y-\mu_{y})^2\right)}},
[/math]
możemy estymować jako
[math] \rho ^{2}=\frac{\left( \underset{i=1}{\overset{N}{\sum }}(x_{i}- \overline{x})(y_{i}-\overline{y})\right) ^{2}}{\underset{i=1}{\overset{N}{ \sum }}(x_{i}-\overline{x})^{2}\underset{i=1}{\overset{N}{\sum }}(y_{i}- \overline{y})^{2}} [/math]
Rozważmy
[math] { \underset{i=1}{\overset{N}{\sum }}(y_{i}^{p}-\overline{y})^{2}=b^{2} \underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x})^{2}=\frac{\left( \underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x})(y_{i}-\overline{y} )\right) ^{2}}{\left( \underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x} )^{2}\right) ^{2}}\underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x} )^{2}=\ } [/math]
[math] { =\frac{\left( \underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x} )(y_{i}-\overline{y})\right) ^{2}}{\underset{i=1}{\overset{N}{\sum }}(x_{i}- \overline{x})^{2}}\frac{\underset{i=1}{\overset{N}{\sum }}(y_{i}-\overline{y} )^{2}}{\underset{i=1}{\overset{N}{\sum }}(y_{i}-\overline{y})^{2}}=\rho ^{2} \underset{i=1}{\overset{N}{\sum }}(y_{i}-\overline{y})^{2}\ } [/math]
czyli
[math] { \rho ^{2}=\frac{\underset{i=1}{\overset{N}{\sum }}(y_{i}^{p}- \overline{y})^{2}}{\underset{i=1}{\overset{N}{\sum }}(y_{i}-\overline{y})^{2} }\ } [/math]