
Wstep
Zapis cyfrowy i korekcja błędów
Aby zrozumieć, dlaczego łatwość korekcji błędów związana jest z zapisem cyfrowym, przyjrzyjmy się bliżej analogowym i cyfrowym zapisom dźwięku. Na płycie analogowej dźwięk kodowany jest w zmiennym wyżłobieniu rowka, w którym przemieszcza się igła gramofonu. W przybliżeniu możemy wyobrazić sobie, że "podskok" igły w większym wgłębieniu rowka odwzorowywany jest jako większe wychylenie membrany głośnika (po zamianie w impuls elektryczny i przejściu przez wzmacniacz). Tak więc wyżłobienie rowka płyty oryginalnie odwzorowuje dokładnie zapisany dźwięk. Jego zarysowanie lub zabrudzenie wprowadzi przy odtwarzaniu zakłócenia (zwykle trzaski). Jednoznaczne rozróżnienie, które z wyżłobień rowka winylowej płyty odzwierciedlają oryginalny zapis muzyki, a które powstały skutkiem uszkodzeń, jest właściwie niemożliwe, dlatego też muzyka ze starych płyt kojarzy nam się z obecnością trzasków i szumu.[1]
W przypadku zapisu cyfrowego możemy w prosty sposób wykryć fakt wystąpienie zakłóceń. Wyobraźmy sobie, że zapisujemy muzykę jako szereg liczb, opisujących amplitudę fali dźwiękowej mierzoną w ustalonych odstępach czasu (rys. Figure 2; dla płyty kompaktowej [math]\Delta t = 1/44 100[/math] sekundy). Ponieważ urządzenie, które będzie zamieniać ten zapis z powrotem na muzykę, i tak musi być swego rodzaju specjalizowanym komputerem (odtwarzaczem CD), to do programu odtwarzającego możemy wprowadzić pewną modyfikację. Umówmy się dla przykładu, że z każdych dziesięciu kolejnych liczb, do zapisu muzyki będziemy wykorzystywać tylko dziewięć, a ostatnią będziemy dobierać tak, żeby suma kolejnych dziesięciu liczb zawsze wynosiła np. milion.
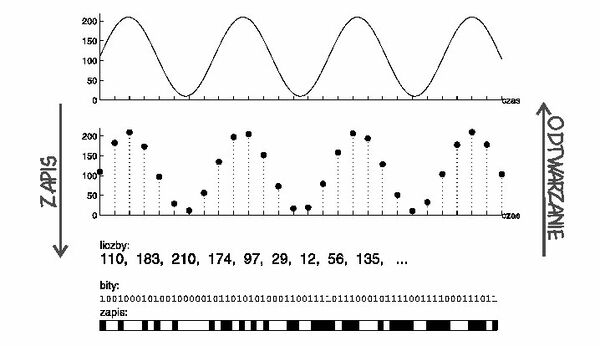
Taki sposób zapisu wprowadza redundancję, czyli nadmiar informacji w zapisie, ponieważ przy prawidłowym odczycie wystarczyłoby znać dziewięć kolejnych liczb, aby wyznaczyć dziesiątą (jako milion minus suma pozostałych dziewięciu). Jednak jeśli wczytamy z takiego zapisu wszystkie liczby, i suma którejś dziesiątki okaże się inna niz milion, to mamy pewność, że w tym miejscu wystąpił błąd.[2] Taka informacja jest bardzo cenna:
- Jeśli jesteśmy pewni , że nagły skok amplitudy w kilku kolejnych próbkach jest wynikiem błędu zapisu, a nie efektem zamierzonym przez muzyka, to możemy ten skok "przemilczeć", czyli np. zastąpić "popsute" próbki średnią wartością poprzednich.
- Możemy zwiększyć redundancję i zapisać dwie jednakowe kopie; jeśli uszkodzeniu ulegnie fragment pierwszej kopii, program może automatycznie sięgnąć do odpowiedniego fragmentu drugiej kopii[3].
- W przypadku transmisji przez modem, program może zażądać powtórnego przesłania uszkodzonego fragmentu.
Niezależnie od tych korzyści, jeśli chcemy analizować sygnały z pomocą komputera (maszyny cyfrowej), i tak jesteśmy "skazani" na pracę z ich dyskretną formą.
Mimo tego, większość ogólnych twierdzeń będziemy rozważać w przestrzeni funkcji ciągłych — o ile nie tyczą się explicite efektów próbkowania. Teoria funkcji ciągłych jest asymptotycznie zgodna z wynikami dla sekwencji dyskretnych — dla odstępu próbkowania dążącego do zera. Jej rezultaty, prostsze pojęciowo i łatwiejsze do wyprowadzenia, są wystarczająco dokładne by wyjaśnić ogólne własności dyskretnych obliczeń.
W uzasadnionych przypadkach będziemy oczywiście dyskutować efekty próbkowania; w takich sytuacjach będziemy rozróżniać sygnał ciągły [math]s(t)[/math] od dyskretnej sekwencji [math]s[n][/math].
Podobne tematy opisuje rozdział "Cyfrowy Świat" z podręcznika Technologii Informacyjnej.
- ↑ Tak naprawdę sprawa nie
jest beznadziejna:
- część zakłócen pochodzi z zanieczyszczeń; w tym przypadku zwykle pomaga delikatne czyszczenie płyty.
- Do pozostałych zakłóceń, których nie da się usunąć mechanicznie, stosuje się potężną metodologię analizy sygnałów (będącą przedmiotem następnych rozdziałów), która pomaga zgadnąć, które dźwięki w zapisie mogą pochodzić z zakłóceń. Zwykle jednak nie da się usunąć dokładnie wszystkich zakłóceń bez naruszenia brzmienia oryginału.
- ↑ Ale poprawna suma nie daje gwarancji, że błędu nie ma. W jednej dziesiątce mogą wystąpić np. dwa jednakowe błędy o przeciwnych znakach i suma pozostanie niezmieniona. Dlatego sumy kontrolne liczy się w bardziej wyrafinowany sposób (np. CRC -- Cyclic Redundancy Check )
- ↑ Prawdopodobieństwo wystąpienia uszkodzeń w tych samych fragmentach dwóch zapisów jest już bez porównania mniejsze niż pojedynczego uszkodzenia. Sposobem wprowadzania nadmiarowości, który minimalizuje prawdopodobieństwo wystąpienia takich pechowych przypadków, rządzi dość złożona matematyka z pogranicza statystyki, której nie będziemy tu omawiać. W każdym razie, dwie jednakowe kopie umieszczone jedna za drugą zwykle nie okazują się rozwiązaniem otymalnym.