Pracownia Biofizyki dla Zaawansowanych/Ćw 3/II

Wyznaczanie współczynników dyfuzji i sedymentacji wybranych białek metodą ultrawirowania analitycznego

dr Anna Modrak-Wójcik

Wstęp

Celem ćwiczenia jest przeprowadzenie eksperymentów ultrawirowania analitycznego wybranego białka. Na ich podstawie określisz homogenność próbki, wyznaczysz współczynniki dyfuzji i sedymentacji tego białka, określisz jego masę i kształt oraz zbadasz wpływ warunków denaturujących na te parametry. Ultrawirowanie analityczne umożliwia charakterystykę makrocząsteczek biologicznych w ich stanach natywnych w roztworze, czyli w warunkach najbardziej zbliżonych do warunków panujących w komórkach, bez istnienia zaburzających oddziaływań, np. z matrycami (chromatografia, elektroforeza), czy powierzchniami (mikroskopia sił atomowych). Dostarcza informacji na temat jednorodności próbki (zanieczyszczenia, oligomery, agregaty), pozwala na określenie masy i kształtu makrocząsteczek. Umożliwia też badania tworzenia się i rozpadu kompleksów oraz wyznaczanie stałych równowagi dla asocjujących układów. Ze względu na zautomatyzowanie sposobu zbierania danych i ich obróbki oraz pojawienie się nowych programów obliczeniowych i szybkich komputerów, metody ultrawirowania, zapoczątkowane na początku ubiegłego stulecia, przeżywają obecnie swój renesans.

Dyfuzja i sedymentacja

Przemieszczanie się cząsteczek w roztworze przy braku sił zewnętrznych jest wywołane dyfuzją. Energia cieplna powoduje, że cząsteczki wykonują nieustanne chaotyczne ruchy, nazywane ruchami Browna. Proces dyfuzji opisuje pierwsze prawo Fick’a:

[math]J_x = -D\frac{\partial c}{\partial x},[/math]

gdzie: [math]J_x[/math] — strumień masy (liczba cząsteczek przechodząca przez jednostkową powierzchnię w jednostce czasu), [math]D[/math] — współczynnik dyfuzji translacyjnej, [math]c[/math] — stężenie cząsteczek. Wynika z niego, że strumień masy jest proporcjonalny do gradientu stężenia [math]\left(\frac{\partial c}{\partial x}\right)[/math]. Znak minus oznacza, że przepływ odbywa się z obszaru o większym stężeniu do obszaru o mniejszym stężeniu. Dyfuzja zapewnia równomierny rozkład stężenia cząsteczek w dostępnej dla nich objętości.

Skomplikowane obliczenia hydrodynamiczne prowadzą do wyrażenia opisującego współczynnik dyfuzji:

[math]D=\frac{RT}{fN_\mathrm{A}}[/math]

gdzie [math]R[/math] — stała gazowa, [math]T[/math] — temperatura w Kelwinach, [math]f[/math] — współczynnik tarcia translacyjnego, [math]N_\mathrm{A}[/math] – liczba Avogadro.

Sedymentacja (osiadanie) to ruch cząsteczek w roztworze pod wpływem zewnętrznej siły. Warunkiem jej zachodzenia są różne wartości gęstości cząsteczek rozpuszczonych i rozpuszczalnika. Przykładem sedymentacji jest opadanie cząsteczek skrobi w świeżo przygotowanej zawiesinie skrobi w zimnej wodzie pod wpływem pola grawitacyjnego. Pole grawitacyjne jest jednak zbyt słabe, by wywołać sedymentację cząsteczek o masach mniejszych niż 10⁷ Da — ze zjawiskiem sedymentacji konkuruje bowiem dyfuzja. Osiadanie cząsteczek o masach odpowiadających masom makrocząsteczek biologicznych wywołują siły odśrodkowe stosowane w wirówkach. Współczesne ultrawirówki analityczne umożliwiają osiągnięcie przyspieszeń odśrodkowych równych 290 000 g i obserwację sedymentacji cząsteczek o masach rzędu kilku kDa. Szczegółowy opis zasady działania ultrawirówki analitycznej znajdziesz w instrukcji do ćwiczenia PB5 w ramach Pracowni Podstaw Biofizyki.

Podstawy fizyczne ultrawirowania

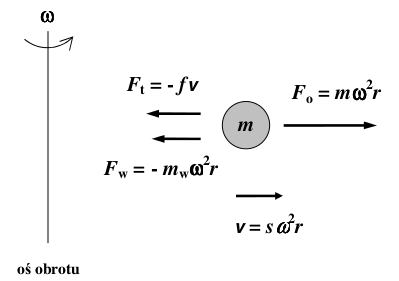
Na cząsteczkę o masie [math]m[/math] znajdującą się w roztworze poddaną wirowaniu z prędkością kątową [math]\omega[/math] działają następujące siły: siła odśrodkowa [math]F_\mathrm{o}[/math], siła wyporu [math]F_\mathrm{w}[/math] oraz siła tarcia dynamicznego [math]F_\mathrm{t}[/math]. Siły te opisane są przez wyrażenia zamieszczone na poniższym schemacie:

gdzie [math]f[/math] to współczynnik tarcia translacyjnego, [math]v[/math] — prędkość ruchu cząsteczki, [math]m_\mathrm{w}[/math] — masa wypartej przez cząsteczkę cieczy, [math]r[/math] — odległość cząsteczki od osi obrotu. Znaki „–” przed siłami tarcia i wyporu wskazują, że siły te działają w przeciwnym kierunku do siły odśrodkowej.

W ciągu bardzo krótkiego czasu (rzędu 10^-6 s) siły te równoważą się, a warunek równoważenia się sił prowadzi do tożsamości będącej definicją współczynnika sedymentacji [math]s[/math] jako prędkości cząsteczki na jednostkę przyspieszenia odśrodkowego:

[math]s\equiv \frac{v}{\omega^2r}=\frac{m(1-\bar{v}\rho)}{f} = \frac{M(1-\bar{v}\rho)}{f N_\mathrm{A}}\;[/math]

gdzie [math]M[/math] — masa molowa cząsteczki, [math]\bar{v}[/math] — cząstkowa objętość właściwa cząsteczki (objętość przypadająca na jednostkę masy), [math]\rho[/math] — gęstość cieczy (rozpuszczalnika), [math]N_\mathrm{A}[/math] — liczba Avogadro [math](m = \nicefrac{M}{N_\mathrm{A}})[/math].

Współczynnik sedymentacji zależy jedynie od parametrów opisujących badaną molekułę i rozpuszczalnik — od masy molowej i cząstkowej objętości właściwej makrocząsteczki, od współczynnika tarcia (a co za tym idzie od kształtu cząsteczki i lepkości rozpuszczalnika) oraz od gęstości rozpuszczalnika. Współczynnik sedymentacji wyrażamy w Svedbergach,

1 Svedberg [S] = 10^-13 sekundy.

Proces sedymentacji pod wpływem siły odśrodkowej można opisać makroskopowo posługując się pojęciem strumienia masy, wprowadzając do równania Fick’a (Equation 1) człon zawiązany z osiadaniem:

[math]J = s\omega^2rc-D\frac{\partial c}{\partial r}[/math]

Po uwzględnieniu zasady zachowania masy i sektorowego kształtu naczynka wirówkowego otrzymujemy wyrażenie:

[math]\frac{\partial c}{\partial t} = \frac{1}{r}\frac{\partial }{\partial r} \left(rD \frac{\partial c}{\partial r} -s \omega^2r^2c\right)[/math]

Jest to równanie różniczkowe wyprowadzone w 1929 r. przez Lamma. Opisuje ono ewolucję czasową rozkładu stężenia próbki zawierającej cząsteczki o współczynnikach sedymentacji [math]s[/math] i dyfuzji [math]D[/math] podczas wirowania z prędkością kątową [math]\omega[/math]. Oprócz szczególnych przypadków, równania Lamma nie można rozwiązać w sposób analityczny.

Korzystając z równania (Equation 2) opisującego współczynnik dyfuzji [math]D[/math] oraz z zależności (Equation 3) otrzymujemy równanie Svedberga:

[math]M=\frac{RTs}{D(1-\bar{v}\rho)}\;[/math]

Wynika z niego, że pomiary współczynników sedymentacji i dyfuzji umożliwiają wyznaczenie masy molowej makrocząsteczki.

Typy eksperymentów ultrawirowania i płynące z nich informacje

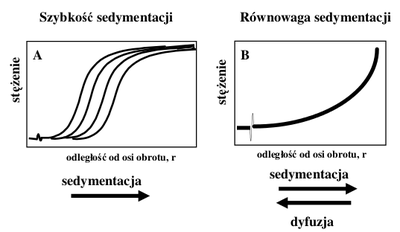
Istnieją dwa typy doświadczeń wykonywanych za pomocą ultrawirówek analitycznych: eksperyment szybkości sedymentacji (sedimentation velocity) i równowagi sedymentacyjnej (sedimentation eqilibrium). W pierwszym z nich próbkę, początkowo jednolitą pod względem rozkładu stężenia, poddaje się działaniu znacznych sił odśrodkowych, co powoduje przesuwanie się cząsteczek rozpuszczonych w kierunku dna kuwety i powstanie ostrej granicy miedzy rozpuszczalnikiem i roztworem (Rys. Figure 1A). Granica ta przemieszcza się z prędkością określoną przez szybkość sedymentacji badanej makrocząsteczki. Rejestracja rozkładu stężenia próbki wzdłuż kuwety w funkcji czasu umożliwia wyznaczenie parametrów hydrodynamicznych: współczynnika sedymentacji, współczynnika dyfuzji (z rozmywania się granicy w czasie), współczynnika tarcia (z równania Equation 2), a także masy molowej (z równania Svedberga).

Porównanie dwóch typów eksperymentów ultrawirowania

Drugi ze wspomnianych eksperymentów — pomiar równowagi sedymentacyjnej — przeprowadzany jest przy nieco niższych prędkościach obrotowych. Po odpowiednio długim czasie (rzędu kilkunastu-kilkudziesięciu godzin) dochodzi do ustalenia się równowagi między procesem sedymentacji i dyfuzji. Powstaje gradient stężenia cząsteczek rozpuszczonych (Rys. Figure 1B), którego rozkład w równowadze nie zależy od czasu. Analiza danych doświadczalnych prowadzi do określenia równowag asocjacyjnych oraz mas cząsteczkowych składników kompleksów. W ramach niniejszego ćwiczenia przeprowadzisz pierwszy z dwóch typów eksperymentów ultawirowania — eksperyment szybkości sedymentacji.

Parametry hydrodynamiczne a kształt cząsteczki

Zarówno współczynnik dyfuzji [math]D[/math] jak i sedymentacji [math]s[/math] zależą od współczynnika tarcia translacyjnego [math]f[/math] (równania Equation 2 i Equation 3), który z kolei pozostaje w ścisłym związku z kształtem poruszającej się cząsteczki. W przypadku gdy cząsteczka jest kulą o promieniu [math]R_\mathrm{S}[/math] współczynnik tarcia opisuje wzór Stokesa:

[math]f_0 = 6\pi\eta R_\mathrm{s} = 6\pi \eta\left(\frac{3M\bar{v}}{4\pi}\right)^{\frac{1}{3}}[/math]

Ze względu na to, że siła tarcia zależy od pola powierzchni badanej cząsteczki, a sfera ma najmniejszą powierzchnię spośród wszystkich brył geometrycznych o tej samej objętości, współczynniki tarcia cząsteczek sferycznych są zawsze mniejsze niż niesferycznych.

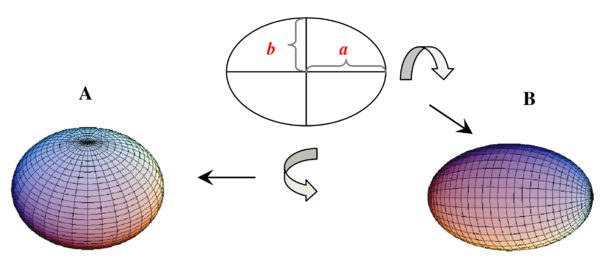
Kształt większości makrocząsteczek biologicznych odbiega od kształtu idealnej kuli. Można jednak zmodyfikować wzór (Equation 7) tak by opisywał współczynnik tarcia f cząsteczek o kształcie spłaszczonej lub wydłużonej elipsoidy obrotowej (Rys. Figure 2).

Elipsoidy obrotowe: (A) spłaszczona (powstająca poprzez obrót elipsy wokół osi małej) i (B) wydłużona (powstająca poprzez obrót elipsy wokół osi wielkiej)

Parametrami charakteryzującymi elipsoidę obrotowej są długości dwóch osi symetrii — wielkiej [math](2a)[/math] i małej [math](2b)[/math]. Wartości stosunku [math]\nicefrac{f}{f_0}[/math] w zależności od wartości stosunku [math]\nicefrac{a}{b}[/math] dla elipsoid wydłużonych i spłaszczonych zostały po raz pierwszy obliczone przez Perrina i są dostępne w formie tabel i za pośrednictwem programów do analizy danych sedymentacyjnych. Na przykład dla wartości stosunku [math]\nicefrac ab = 5\ \nicefrac{f}{f_0} =1,25\ \text{lub} 1,22[/math] odpowiednio dla elipsoidy wydłużonej i spłaszczonej. Wartość stosunku [math]\nicefrac{f}{f_0}[/math] jest więc miarą stopnia asymetrii badanej makrocząsteczki, stopnia w jakim jej kształt odbiega od kształtu sferycznego (dla sfery [math]\nicefrac ab = 1[/math]).

Na podstawie eksperymentu szybkości sedymentacji można uzyskać informacje dotyczące kształtu badanej cząsteczki. Wartość współczynnika tarcia f można wyznaczyć na podstawie zależności (Equation 3):

[math]f = \frac{M(1-\bar{v}\rho)}{sN_\mathrm{A}}[/math]

Porównując ją z wartością [math]f_0[/math] określoną równaniem (Equation 7) otrzymujemy stosunek [math]\nicefrac{f}{f_0}[/math].

Metody wyznaczanie współczynników sedymentacji i dyfuzji na podstawie eksperymentu szybkości sedymentacji

Istnieje kilka metod wyznaczania współczynników sedymentacji i dyfuzji na podstawie eksperymentów szybkości sedymentacji. W ramach Pracowni Podstaw Biofizyki została przedstawiona metoda „punktu środkowego” (midpoint method), w której współczynnik sedymentacji oblicza się poprzez pomiar położenia środka granicy w funkcji czasu. Nie pozwala ona jednak na określenie współczynnika dyfuzji, a co za tym idzie masy i kształtu makrocząsteczki. Pełna analiza wymaga wykorzystania informacji o czasowej ewolucji kształtu granicy. Można to osiągnąć dzięki zastosowaniu zaawansowanych algorytmów, pozwalającym na numeryczne rozwiązanie równania Lamma (Equation 5). Obecnie dostępnych jest kilka niekomercyjnych programów wykorzystujących różne podejścia do analizy danych doświadczalnych.

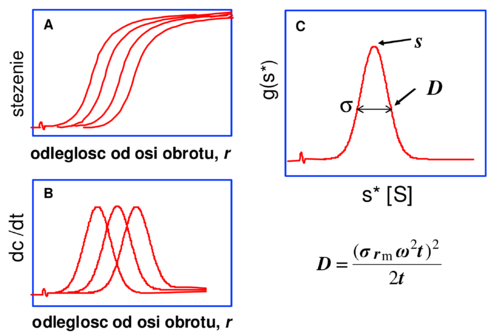
Jedną z często stosowanych procedur jest metoda pochodnej czasowej opracowana w 1992 r. przez Waltera Stafforda. W oparciu o tę metodę działa program DCDT⁺ stworzony przez Johna Philo (http://www.jphilo.mailway.com/dcdt+.htm). Program wyznacza pochodne czasowe rozkładów stężenia na podstawie radialnych dystrybucji otrzymanych w eksperymencie, odejmując parami kolejne rozkłady [math](\Delta c)[/math] i dzieląc przez odpowiadający im odstęp czasowy [math](\Delta t)[/math]. Następnie przeskalowuje je, uniezależniając od czasu. Ostatecznie otrzymujemy rozkład, zwany [math]g(s*)[/math], mówiący o populacji cząsteczek o danym współczynniku sedymentacji. Zakładając gaussowską postać rozkładu [math]g(s*)[/math], z maksimum tego rozkładu można odczytać współczynnik sedymentacji, a z szerokości połówkowej współczynnik dyfuzji (Rys. Figure 3).

Obecnie coraz większą popularnością cieszy się program SEDFIT stworzony pod koniec ubiegłego stulecia przez Petera Schucka z National Institutes of Health oferujący różne modele do analizy danych (http://www.analyticalultracentrifugation.com). Jednym z modeli jest ciągły rozkład współczynnika sedymentacji [math]c(s)[/math] zdefiniowany jako:

[math]a(r,t) = \int c(s)L(s,D(s),r,t)\mathrm ds[/math]

gdzie [math]a(r, t)[/math] to profile radialne stężenia uzyskane podczas eksperymentu ultrawirowania, [math]c(s)[/math] odpowiada populacji cząsteczek o współczynniku sedymentacji pomiędzy [math]s[/math] a [math]s+\mathrm ds[/math], a [math]L(s, D(s), r, t)[/math] to rozwiązanie równania Lamma (Equation 5) dla cząsteczek o współczynniku sedymentacji [math]s[/math] i dyfuzji [math]D[/math].

Zasadniczo, analiza danych przy użyciu równania (Equation 9) sprowadza się do znalezienia optymalnej kombinacji dużej liczby rozwiązań równania Lamma najlepiej pasującej do danych doświadczalnych. Założeniem modelu przy wyznaczaniu wartości współczynnika dyfuzji [math]D(s)[/math] dla cząsteczek o danym współczynniku sedymentacji [math]s[/math] jest, że wszystkie rodzaje sedymentujących cząsteczek mają tę samą wartość stosunku [math]\nicefrac{f}{f_0}[/math]. Stosunek [math]\nicefrac{f}{f_0}[/math] jest parametrem dopasowania. Zastosowanie równania Svedberga (Equation 6) dla każdej z par [math]s[/math] i [math]D(s)[/math] prowadzi do transformacji rozkładu [math]c(s)[/math] do rozkładu mas molowych [math]c(M)[/math].

Ilustracja kolejnych kroków metody pochodnej czasowej Stafforda, prowadzących do otrzymania współczynników sedymentacji i dyfuzji

W ramach niniejszego ćwiczenia analizę danych z eksperymentów szybkości sedymentacji przeprowadzisz za pomocą programu SEDFIT.

Parametry hydrodynamiczne w warunkach standardowych

Tak jak już wcześniej wspomniano, współczynnik sedymentacji zależy od gęstości rozpuszczalnika oraz lepkości roztworu. Wielkości te z kolei zależą od temperatury. Podobnie jest w przypadku współczynnika dyfuzji — na jego wartość również wpływ ma temperatura i lepkość roztworu. Aby móc porównywać ze sobą wartości współczynników [math]s[/math] i [math]D[/math] uzyskane w różnych warunkach eksperymentalnych (temperatura, bufor), przelicza się uzyskane wartości dla tzw. warunków standardowych, czyli dla wody w 20 °C zgodnie z zależnościami:

[math]s_{20,\mathrm w} = s\frac{(1-\bar{v}\rho)_{20,\mathrm w}}{(1-\bar{v}\rho)_{T,b}}\cdot \frac{\eta_{T,b}}{\eta_{20,\mathrm w}}[/math]

[math]D_{20,\mathrm w} = D\frac{273,15}{T}\cdot \frac{\eta_{T,b}}{\eta_{20,\mathrm w}}[/math]

Indeks T,b odnosi się do wartości cząstkowej objętość właściwej makrocząsteczki [math](\bar{v})[/math], gęstości [math](\rho)[/math] i lepkości [math](\eta)[/math] buforu w temperaturze, w której przeprowadzono dany eksperyment [math](T)[/math]; indeks 20,w oznacza warunki standardowe (woda, 20 °C).

Należy też pamiętać, że współczynnik sedymentacji zależy od stężenia próbki. Homogenne, nie asocjujące cząsteczki wykazują spadek współczynnika sedymentacji wraz ze wzrostem stężenia. Efekt ten jest niewielki dla białek globularnych, staje się znaczący dla cząsteczek o wydłużonym kształcie lub zdenaturowanych. Wywołany jest wzrostem lepkości roztworu przy wyższych stężeniach badanej próbki.

Wymagania do kolokwium wstępnego

1. Zjawisko absorpcji promieniowania elektromagnetycznego, prawo Lamberta-Beera.
2. Podstawy fizyczne ultrawirowania: wyprowadzenie równania Svedberga, definicja współczynnika sedymentacji, równanie Lamma.
3. Zasada działania ultrawirówki analitycznej: różnice między wirowaniem analitycznym i preparatywnym, metody detekcji sedymentujących cząsteczek i zakres ich stosowalności, budowa kuwet pomiarowych.
4. Typy eksperymentów ultrawirowania.
5. Zastosowanie metod ultrawirowania w badaniach makrocząsteczek biologicznych.
6. Wpływ warunków denaturujących na strukturę białek.

Wykonanie ćwiczenia

Podczas ćwiczenia przeprowadzisz dwa eksperymenty ultrawirowania typu szybkości sedymentacji dla albuminy z krwi wołu (BSA) przy użyciu ultrawirówki analitycznej XL-I firmy Beckman Coulter. Rozkład stężenia podczas wirowania będziesz monitorować stosując detekcję interferencyjną i absorpcyjną.

Masz do dyspozycji:

• albuminę z krwi wołu w proszku (BSA),
• 20 mM bufor Tris-HCl pH 7,0 zawierający 0,1 M NaCl (bufor A),
• 20 mM buforze Tris-HCl pH 7,0 zawierający 0,1 M NaCl i 6 M chlorowodorek guanidyny (bufor B).

Dzień pierwszy:

1. Przygotuj roztwór albuminy o stężeniu 2.5 mg/ml w buforze A (~ 1.5 ml). Roztwór przygotuj z naważki a następnie oznacz jego stężenie spektrofotometrycznie. Współczynnik ekstynkcji albuminy wynosi [math]\varepsilon^{0,1\%}(280) = 0,667[/math] ([math]\varepsilon^{0,1\%}[/math] odpowiada absorbancji 0,1% roztworu, czyli 1mg/ml, w kuwecie o drodze optycznej 1 cm).
2. Roztwór BSA z pkt. 1 wykorzystaj do przygotowania trzech próbek albuminy w buforze A (potrzebne będzie po ~ 0,5 ml każdej) o absorbancjach w kuwecie o drodze optycznej 1,2 cm równych odpowiednio 0,2, 0,5 i 1,0.
3. Następny krok to przygotowanie, napełnienie i załadowanie kuwet z próbkami do rotora. Ten etap eksperymentu zostanie wykonany przez asystenta. Szczegółowy opis budowy i sposobu przygotowania kuwet do eksperymentu ultrawirowania znajdziesz w instrukcji do ćwiczenia PB5. Użyjemy dwusektorowych części centralnych o drodze optycznej 12 mm oraz 4-dziurowego rotora. Po skręceniu, każdą z trzech kuwet (mamy trzy próbki — patrz pkt. 2) napełniamy w sposób następujący: lewy sektor — 400 μl buforu, prawy sektor – 390 μl białka (kuwetę kładziemy nakrętką w naszą stronę). Różne wartości objętości buforu i roztworu białka pozwalają na równoczesną obserwację obu menisków, co z kolei umożliwia wykrycie nieszczelności kuwety. Po umieszczeniu rotora z próbkami w komorze wirówki, montujemy monochromator, zasuwamy pokrywę i uruchamiamy pompę próżniową poprzez wciśnięcie przycisku VACUUM na panelu wirówki.
4. Z pomocą asystenta, w programie sterującym ultrawirówką ustaw parametry eksperymentu:
   • temperatura 20 °C,
   • obroty 42 000 rpm,
   • detekcja absorpcyjna w 280 nm,
   • detekcja interferencyjna,
   • rejestracja rozkładów radialnych co 5 minut,
   • całkowita liczba zarejestrowanych rozkładów danego typu (absorpcja lub interferencja) dla każdej z próbek &,dash; 200
     i zapisz ustawione parametry jako nową metodę.
5. Czekając na ustalenie się próżni i temperatury, wykonaj przy niskich obrotach rotora (3000 rpm) widma absorpcyjne próbek w zakresie 240-320 nm dla wybranego punktu kuwety (np. dla r = 6,5 cm, r to odległość od osi obrotu; kuweta „rozciąga się” w zakresie 5,8-7,2 cm). Zarejestruj również profile radialne każdej z próbek w 280 nm. Czy rozkład stężenia w białka w kuwetach jest jednorodny? Czy absorbancja w 280 nm jest zgodna z Twoimi wcześniejszymi obliczeniami?
6. Po ustaleniu się próżni i temperatury zatrzymaj wirówkę, wyzeruj czas na panelu wirówki, wpisz właściwą liczbę obrotów w programie sterującym (42000 rpm) i ponownie uruchom wirówkę. Gdy rotor osiągnie zadaną prędkość odczekaj 15-30 s i rozpocznij eksperyment.

Ponieważ wirowanie potrwa kilkanaście godzin zatrzymamy wirówkę następnego dnia rano.

Dzień drugi: Powtórz czynności z dnia pierwszego. Tym razem jednak do przygotowania roztworu BSA użyj buforu B (z chlorowodorkiem guanidyny).

Opracowanie danych

Do analizę danych z dwóch powyższych eksperymentów wykorzystaj programu SEDFIT (http://www.analyticalultracentrifugation.com). Zastosuj model [math]c(s)[/math]. Potrzebna Ci będzie znajomość wartości cząstkowej objętości właściwej BSA oraz gęstości i lepkości stosowanych buforów. Do wyliczania tych wielkości użyj ogólnie dostępnego programu SEDNTERP (http://jphilo.mailway.com/download.htm). Pozwala on na wyznaczenie lepkości i gęstości roztworów składających się z różnych komponentów i w różnych temperaturach oraz cząstkowej objętości właściwej białek na podstawie ich składu aminokwasowego. Sekwencję BSA (Bovine Serum Albumin) znajdziesz w bazie UniProt (http://www.uniprot.org/).

Opracowanie wyników powinno uwzględniać następujące zagadnienia:

1. Wyznaczenie rozkładu współczynnika sedymentacji [math]c(s)[/math] dla każdej z próbek.
2. Określenie stopnia homogenności próbki (BSA znane jest ze skłonności do tworzenia dimerów i oligomerów wyższych rzędów).
3. Określenie współczynników sedymentacji, dyfuzji, mas oraz asymetrii poszczególnych populacji cząsteczek.
4. Porównanie otrzymanych wartości mas z masą BSA obliczoną na podstawie sekwencji aminokwasowej (UniProt) oraz interpretację uzyskanych wyników.
5. Analizę wpływu stężenia BSA w próbce na wartości współczynnika sedymentacji.
6. Analizę wpływu warunków denaturujących na parametry hydrodynamiczne.

Opis końcowy

Opis końcowy powinien zawierać poszczególne elementy charakterystyczne dla raportu z przebiegu eksperymentu (streszczenie, wstęp teoretyczny, opis układu doświadczalnego oraz wyniki i ich dyskusję). Opracowanie wyników powinno uwzględniać zagadnienia wyszczególnione powyżej i zostać udokumentowane za pomocą czytelnych tabel i wykresów.

Literatura

1. Materiał z zakresu ultrawirowania, przedstawiony w trakcie wykładu i ćwiczeń „Metody biofizyki molekularnej”, B. Wielgus-Kutrowska
2. „Ultrawirowanie analityczne — wyznaczanie współczynnika sedymentacji albuminy z krwi wołu (BSA)”, A. Modrak-Wójcik — opis do ćwiczenia PB5 w ramach Pracowni Podstaw Biofizyki
3. „Biofizyka. Wybrane zagadnienia wraz z ćwiczeniami”, red. Z. Jóźwiak i G. Bartosz, PWN 2007
4. „Biofizyka molekularna”, Genowefa Ślósarek, PWN 2011
5. „Modern analytical ultracentrifugation in protein science: A tutorial review”, J. Lebowitz, M. S. Lewis, P. Schuck, Prot. Science 11, pp. 2067-2079, 2002