Fizyka I FM/Kinematyka1

Wstęp

Ruch prostoliniowy jest to ruch, w którym wektor prędkości ma stały kierunek w przestrzeni. Równanie każdego ruchu prostoliniowego można przedstawić w postaci:

[math] \vec{r}(t)=\vec{r}_0+f(t)\vec{d} [/math]

Ilustracja do zagadnienia ruchu prostoliniowego.

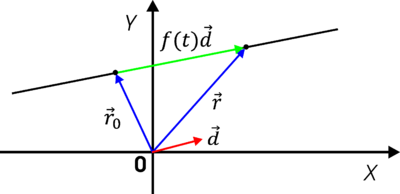
gdzie niezalezny od czasu wektor [math]d[/math] ma wartość równą 1. Jest to to równanie parametryczne prostej przechodzącej przez punkt o wketorze położenia [math]\vec{r}_0[/math] i równoległej do wektora [math]d[/math] — rysunek %i 1. Rolę parametru pełni funkcja czasu f(t):

[math] \vec{V}=\frac{df(t)}{dt}\vec{d} [/math]

Wektor prędkości ma w każdej chwili ten sam kierunek w przestrzeni i jest równoległy do stałego wektora [math]\vec{d}[/math]. Wektor przyspieszenia ma również stały kierunek w przestrzeni — przyspieszenie ma tylko składową styczna do toru. Przyspieszenie normalne jest równe 0.

[math] \vec{a}=\frac{d^2f(t)}{dt^2}\vec{d} [/math]

Wygodnie jest traktować prostą wzdłuż której odbywa się ruch jako oś liczbową o wektorze jednostkowym [math]\vec{d}=\vec{e}_x[/math]. Do opisu położenia (ruchu) wystarcza wtedy znajomość jednej współrzędnej x punktu na torze, zaś ruch opisany jest równaniami:

[math] \begin{array}{l} x(t) = x_0 + f(t) \\ \\ V_x = \frac{dx}{dt}=\frac{df(t)}{dt} \\ \\ a_x = \frac{dV_x(t)}{dt} = \frac{d^2x(t)}{dt^2} \end{array} [/math]

Każdy ruch można traktować jako wynik złożenia ruchów prostoliniowych — w najogólniejszym przypadku wzdłuż trzech nierównoległych i niewspółpłaszczyznowych prostych (w ruchu płaskim — wzdłuż nierównoległych prostych na płaszczyźnie).

Ruch jednostajny prostoliniowy

Z założenia jest to ruch odbywający się ze stałą prędkością, tzn. wektor prędkości nie zmienia kierunku (ruch prostoliniowy) ani wartości (ruch jednostajny):

[math] \vec{V}=\text{const} [/math]

czyli:

[math] \begin{array}{l} V = \text{const}\\ \\ \frac{\vec{V}}{V}= \overrightarrow{\text{const}}\\ \\ \vec{a}=0 \end{array} [/math]

Jeśli dobierzemy układ współrzędnych tak, by oś X pokrywała się z torem ruchu, wtedy położenie ciała możemy określić przy pomocy następującego wzoru:

[math] x=x_0+V(t-t_0) [/math]

Ruch jednostajny przyspieszony

Z założenia jest to ruch, w który wektor przyspieszenia ma zarówno stałą wartość jak i kierunek:

[math] \vec{a} = \text{const} [/math]

Prędkość w ruchu jednostajnie przyspieszonym opisuje poniższy wzór:

[math] \vec{V} = \vec{V}_0 + \vec{a}(t-t_0) [/math]

Szczególnym przypadkiem ruchu jednostajnie przyspieszonego jest ruch jednostajnie przyspieszony prostoliniowy, w przypadku którego wektor przyspieszenia jest równoległy do wektora prędkości — [math]\vec{V}||\vec{a}[/math]. Innymi słowy, w ruchu tym zmienia się tylko wartość wektora prędkości, natomiast jego kierunek jest stały (czyli [math]\frac{\vec{V}}{V} = \overrightarrow{\text{const}}[/math]). W przypadku takiego ruchu, jeśli dobierzemy tak układ współrzędnych, aby oś X układu pokrywała się z torem ruchu, przyspieszenie, prędkość i położenie ciała możemy opisać następującymi równaniami:

[math] \left\{\begin{array}{l} a = \text{const} \\ \\ V = V_0 + a(t-t_0)\\ \\ x = x_0 + (V+V_0)(t-t_0) + \frac{1}{2}a(t-t_0)^2 \end{array}\right. [/math]

W ogólnym przypadku ruchu jednostajnie przyspieszonego, wektory prędkości i położenia opisują następujące wzory:

[math] \left\{\begin{array}{l} \vec{V}=\vec{V}_0+\vec{a}(t-t_0) \\ \\ \vec{r} = \vec{r}_0+\vec{V}_0(t-t_0)+\frac{1}{2}\vec{a}(t-t_0)^2 \end{array}\right. [/math]

Ruch opisane powyższymi równaniami odbywa się w płaszczyźnie przechodzącej przez koniec wektor [math]\vec{r}_0[/math], a wyznaczonej przez wektory [math]\vec{V}_0[/math] i [math]\vec{a}[/math]. Zawsze jest to więc ruch w ustalonej płaszczyźnie.

Zadanie 1.

Odległość między punktami A i B wynosi 80 km. Z punktu A w kierunku B wyjeżdża motocyklista z prędkością [math]v_1 = \unit{50}{\frac{km}{h}}[/math]. Równocześnie z punktu B wyjeżdża w tym samym kierunku samochód z prędkością [math]v_2 = \unit{30}{\frac{km}{h}}[/math]. Kiedy i w jakiej odległości od punktu A motocyklista dogoni samochód? Przedstaw ruch pojazdów na wykresie.

Zadanie 2.

Rowerzysta jadący z prędkością [math]v_1 = \unit{15}{\frac{km}{h}}[/math] spotyka na swojej drodze pieszego. Po [math]t_1 = 1\unit{5}{min}[/math] od spotkania rowerzysta dojeżdża do biblioteki, w której przebywał [math]t_2 = \unit{1}{h}[/math] i 10 minut, po czym z prędkością [math]v_2 = \unit{15}{\frac{km}{h}}[/math] jedzie z powrotem i po czasie [math]t_3 = 30[/math] minut dogadania pieszego. Pieszy idzie cały czas ze stałą prędkością. Określić tę prędkość i przedstawić ruch rowerzysty i pieszego graficznie.

Zadanie 3.

Ilustracja do zadania 3.

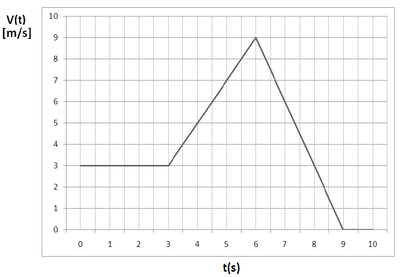
Na rysunku %i 2 przedstawiono wykres prędkości ciała w funkcji czasu. Znajdź zależność a([math]t[/math]) i x([math]t[/math]).

Zadanie 4.

Ilustracja do zadania 4.

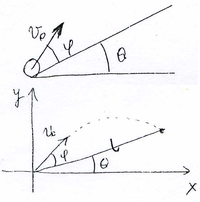
Piłce nadano na progu równi prędkość [math]\vec{V}_0[/math], której wektor skierowany był pod katem [math]\phi[/math] do powierzchni równi (rysunek %i 3). Nachylenie równi do poziomu wynosi [math]\Theta[/math]. Wyznaczyć odległość, mierzoną wzdłuż równi, na jaką przemieści się piłka do momentu zderzenia z równią. Dla jakiego kąta [math]\phi[/math] przy zadanym kącie [math]\Theta[/math] zasięg mierzony wzdłuż równi jest maksymalny?