Fizyka I FM/Dynamika ruchu bryły sztywnej

Ruch punktu materialnego, a ruch bryły sztywnej

Poniżej dokonano zestawienia wielkości, które służą do opisu ruchu punktu materialnego oraz odpowiadające im wielkości w przypadku ruchu obrotowego względem osi symetrii bryły sztywnej.

Punkt materialny ruch postępowy			Bryła sztywna ruch obrotowy względem osi symetrii
przesunięcie	[math]\vec{x}[/math]	→	kąt obrotu	[math]\vec{\phi}[/math]
prędkość	[math]\vec{V}=\frac{d\vec{x}}{dt}[/math]	→	prędkość kątowa	[math]\vec{\omega}=\frac{d\vec{\phi}}{dt}[/math]
przyspieszenie	[math]\vec{a}=\frac{d\vec{V}}{dt}[/math]	→	przyspieszenie kątowe	[math]\vec{\varepsilon}=\frac{d\vec{\omega}}{dt}[/math]
masa	[math]m[/math]	→	moment bezwładności	[math]I[/math]
pęd	[math]\vec{p}=m\vec{V}[/math]	→	moment pędu	[math]\vec{L}=I\vec{\omega}[/math]
układ izolowany	[math]\vec{p}=\text{const}[/math]	→	moment pędu	[math]\vec{L}=I\vec{\omega}[/math]
układ izolowany	[math]\vec{p}=\text{const}[/math]	→	moment pędu	[math]\vec{L}=I\vec{\omega}[/math]
siła	[math]\vec{F}=\text{const}[/math]	→	moment siły	[math]\vec{M}[/math]
równania ruchu	[math]\vec{F}=m\vec{a}[/math] [math]\frac{d\vec{p}}{dt}=\vec{F}[/math]	→	równania ruchu	[math]\vec{M}=I\vec{\varepsilon}[/math] [math]\frac{d\vec{L}}{dt}=\vec{M}[/math]
praca	[math]W=\int\vec{F}\cdot d\vec{x}[/math]	→	praca	[math]W=\int\vec{M}\cdot d\vec{\phi}[/math]

Zadanie 1.

Ilustracja do zadania pierwszego.

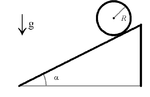
Jednorodny walec o promieniu R stacza się bez poślizgu z równi o kącie nachylenia α — patrz rysunek Figure 1. Policzyć przyspieszenie z jakim porusza się środek masy walca wzdłuż powierzchni równi zakładając, że toczenie jest bezstratne, a natężenie pola siły ciężkości wynosi g. Zadanie rozwiązać dwiema drogami: za pomocą bilansu sił i ich momentów oraz poprzez bilans energii. Uzyskaj wyniki liczbowe dla [math]\alpha[/math]= [math]\pi/6[/math] i m=500g.

Zadanie 2.

Ilustracja do zadania drugiego.

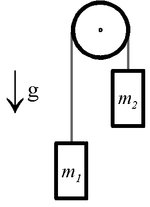
Przez krążek zawieszony na poziomej osi przerzucono nieważką nić, do której końców przymocowano ciężarki o masach [math]m_1[/math] i [math]m_2[/math] ( patrz rysunek Figure 2). Krążek jest jednorodny a jego masa wynosi [math]m_0[/math]. Znajdź przyspieszenie liniowe ciężarków i określ, w którą stronę (zależnie od proporcji ich mas) następuje ten ruch, jeśli układ początkowo spoczywał. Przyjmij że nić nie ślizga się po obrzeżu krążka. Układ znajduje się w jednorodnym polu siły ciężkości o natężeniu g = 10[math]m/s^2[/math]. Tarcie w łożysku krążka należy pominąć. Uzyskaj wyniki liczbowe dla [math]m_1[/math]=300g, [math]m_2[/math]=200g i [math]m_0[/math]=300g.

Zadanie 3.

Ilustracja do zadania trzeciego.

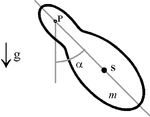
Jednowymiarowe wahadło fizyczne o masie m ma postać bryły sztywnej, która może się obracać jedynie wokół jednej poziomej osi P, której pozycja przestrzenna jest niezmienna — patrz rysunek Figure 3. Odległość środka masy wahadła S od osi P wynosi L, moment bezwładności bryły względem osi rotacji wynosi I, a układ znajduje się w polu siły ciężkości o natężeniu g. Wprowadzając zmienną kątową α opisującą odchylenie wahadła od pozycji jego stabilnej równowagi, napisać równanie ruchu wahadła. Znaleźć częstość wahań układu używając przybliżenia zakładającego, że amplituda tych wahań jest mała α « 1.

Zadanie 4.

Policzyć moment bezwładności jednorodnego krążka o masie m, promieniu R, względem osi przechodzącej przez środek masy:

• wzdłuż osi symetrii obrotowej,
• prostopadle do osi symetrii.

Zadanie 5.

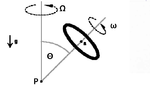
Żyroskop ma postać osiowosymetrycznej bryły sztywnej zamocowanej w punkcie P, leżącym na osi symetrii w odległości L od środka masy bryły S w ten sposób, że bryła może wirować wokół swojej osi, a oś może swobodnie zmieniać kierunek w przestrzeni, przy czym odległość środka masy bryły od punktu zaczepienia nie zmienia się. Moment bezwładności tak zamocowanej bryły względem jej osi symetrii wynosi [math]I_\mathrm{C}[/math], zaś momenty względem osi prostopadłych do osi symetrii i przechodzących przez punkt zaczepienia wynoszą [math]I_\mathrm{A}[/math]. Szczególne rozwiązanie równań ruchu (precesja regularna) ma postać taką, że bryła szybko wiruje wokół osi symetrii, a oś wykonuje relatywnie powolny, jednostajny obrót wokół pionu, zachowując przy tym stały kąt odchylenia od pionu (precesja). Znaleźć częstość [math]\Omega[/math] precesyjnego ruchu osi, jeśli częstość wirowania wokół osi ma wartość [math]\omega[/math], odchylenie osi od pionu wynosi [math]\Theta[/math], pole ma natężenie g, a masa bryły wynosi m. Jaka jest częstość precesji w granicy szybkiego wirowania bryły [math]\omega\gt \gt \Omega[/math]?

Ilustracja do zadania piątego.