Fizyka I FM/Fizyka współczesna
Zadanie 1.(Wsteczne rozpraszanie Comptona na relatywistycznych elektronach.)
W procesie Comptona fotony UV padają na spoczywające elektrony i rozpraszają się, a długość fali zależy jedynie od kąta rozproszenia [math]\Theta[/math]:
[math] \Delta\lambda = \lambda' - \lambda = \frac{h}{m_ec}(1-\cos(\Theta)) = \lambda_c(1-\cos(\Theta)) [/math]
gdzie:
[math]\lambda_c=\frac{h}{m_ec} = \unit{2,4\cdot10^{-3}}{nm}[/math]
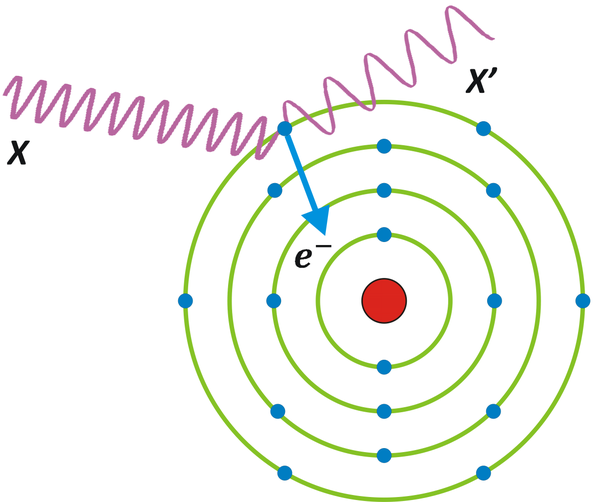
W zderzeniu fotonów z lasera rubinowego ([math]\lambda=\unit{700}{nm}[/math]) z elektronami z akceleratora LEP w CERN-ie o energii [math]E_e=\unit{45}{GeV}[/math], zachodzi rozproszenie do tyłu (rysunek Figure 1). Oblicz energię rozproszonych fotonów.
Zadanie 2. (Efekt Dopplera.)
Przeprowadzono spektrometryczne badania promieniowania pochodzącego z odległej galaktyki. Linię widmowa o długości fali (zarejestrowanej w spektrometrze) [math]\lambda=\unit{730}{nm}[/math] udało się zidentyfikować jako linię wodoru serii Balmera, która w warunkach laboratorium ziemskiego ma długość fali [math]\lambda_0=\unit{487}{nm}[/math]. Korzystając z wzorów Dopplera oblicz prędkość i kierunek ruchu galaktyki.
Zadanie 3. (Efekt Dopplera i stała Hubble’a)
Obserwacje wskazują, że Wszechświat rozszerza się jednorodnie i nie posiada wyróżnionego punktu. Dla odpowiednio dużych skal w porównaniu z rozmiarami Galaktyki spełniona jest zależność (prawo Hubble’a):
[math] V=H_0\cdot r [/math]
gdzie:
- V — prędkość oddalania się obiektu (źródła promieniowania(galaktyki)) od Ziemi,
- r — odległość do źródła,
- [math]H_0[/math] — stała Hubble’a.
Oblicz:
- w jaki sposób stosunek [math]\frac{\lambda}{\lambda_0}[/math] zależy od odległości źródła od Ziemi (r), przy spełnieniu prawa Hubble’a. Oblicz Stałą Hubble’a jako funkcję r i [math]\frac{\lambda}{\lambda_0}[/math].
- W jaki sposób wielkość zdefiniowana jako przesunięcie ku czerwieni [math]z=\frac{\lambda-\lambda_0}{\lambda_0}\rightarrow z=\frac{\Delta\lambda}{\lambda_0}[/math] zależy od odległości źródła od Ziemi (r), przy spełnieniu prawa Hubble’a.
- Policz stałą Hubble’a dla:
- Galaktyka w gwiazdozbiorze Panny [math]r_1=\unit{17}{Mpc}[/math], [math]z_1=\text{0,00}[/math],
- Galaktyka w Wielkiej Niedźwiedzicy [math]r_2=\unit{180}{Mpc}[/math], [math]z_2=\text{0,051}[/math].