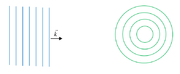Fizyka III/Opis fal w dwóch i trzech wymiarach

Wstęp

W poprzednim rozdziale wspominaliśmy, że fale dźwiękowe rozchodzą się we wszystkich kierunkach. Dlatego równanie falowe oraz funkcja falowa powinna uwzględniać ten fakt. Klasyczne równanie falowe w przestrzeni trójwymiarowej we współrzędnych kartezjańskich ma postać:

[math]\frac{\partial^2\Psi(x,y,z,t)}{\partial x^2}+\frac{\partial^2\Psi(x,y,z,t)}{\partial y^2}+\frac{\partial^2\Psi(x,y,z,t)}{\partial z^2}=\frac 1{v^2}\frac{\partial^2\Psi(x,y,z,t)}{\partial t^2}[/math]

lub uwzględniając operator Laplace’a:

[math]\Delta\Psi(x,y,z,t)=\frac 1{v^2}\frac{\partial^2\Psi(x,y,z,t)}{\partial t^2}[/math]

W wielu zagadnieniach, wygodniej jest używać innego układu współrzędnych. We współrzędnych cylindrycznych laplasjan ma postać:

[math]\Delta\Psi = \frac 1 \rho\frac\partial{\partial\rho}\left(\rho\frac{\partial\Psi}{\partial\rho}\right)+\frac 1{\rho^2}\frac{\partial^2\Psi}{\partial\phi^2}+ \frac{\partial^2\Psi}{\partial z^2}[/math],

Natomiast we współrzędnych sferycznych:

[math]\Delta\Psi = \frac 1 {r^2}\frac\partial{\partial r}\left(r^2\frac{\partial\Psi}{\partial r}\right)+\frac 1{r^2\sin\theta}\frac{\partial}{\partial\theta}\left(\sin\theta \frac{\partial\Psi}{\partial\theta}\right)+ \frac 1{r^2\in^2\theta}\frac{\partial^2\Psi}{\partial\phi^2}[/math]

W przypadku przestrzeni trójwymiarowej są dwa rodzaje rozwiązań klasycznego równania falowego w postaci fali harmonicznej. Pierwszy rodzaj rozwiązania jest następujący: [math]\Psi(x,y,z,t)=\Psi(\vec r,t)=A\cos(\vec k\vec r -\omega t)[/math]. Wektor [math]\vec k[/math] nosi nazwę wektora falowego. Jego długość jest równa: [math]k=\frac{2\pi}\lambda[/math], natomiast jego zwrot określa kierunek rozchodzenia się fali. Czasami falę biegnącą zapisujemy w formie zespolonej: [math]\Psi(\vec r,t)=\mathrm{Re}ae^{i(\vec k\vec r-\omega t)}[/math].

Drugi rodzaj rozwiązania ma postać: [math]\Psi(x,y,z,t)=\Psi(\vec r,t)=A\cos(kr -\omega t)[/math]. Taką falę nazywamy falą kolistą lub kulistą. Fala rozchodzi się izotropowo we wszystkich kierunkach. Na rysunku Figure 1 pokazano czoła fali płaskiej i fali kolistej.

Czoła fali płaskiej (po lewej stronie) i fali kolistej (po prawej stronie).

Należy zwrócić uwagę na bardzo ważny fakt. Średnia moc źródła fali wynosi: [math]P_\mathrm{sr}=\frac 1 2 Z A^2 \omega^2S[/math], co oznacza, że amplituda fali kulistej: [math]A=\sqrt{\frac{2P_\mathrm{sr}}{Z\omega^2 S}}\propto\frac 1\sqrt S[/math].

W przypadku fali rozchodzącej się w przestrzeni dwuwymiarowej amplituda fali maleje z odległością od źródła jak [math]A\propto \frac 1\sqrt r[/math]., natomiast w przestrzeni trójwymiarowej jak [math]A\propto \frac 1r[/math]. A zatem kołowe fale na płaszczyźnie mają postać: [math]\Psi(\vec r,t)=\frac{A_0}{\sqrt r}\cos(kr-\omega t)[/math] a kuliste fale w przestrzeni trójwymiarowej [math]\Psi(\vec r,t)=\frac{A_0} r\cos(kr-\omega t)[/math].

Fale stojące

Teraz zajmiemy się kolejnym zagadnieniem: falami stojącymi. Jako przykład poszukajmy fal stojących w dwuwymiarowej membranie o wymiarach [math]a \times b[/math] zamocowanej na końcach. Szukamy rozwiązania równania [math]\frac{\partial^2\Psi(x,y,z,t)}{\partial x^2}+\frac{\partial^2\Psi(x,y,z,t)}{\partial y^2}+\frac{\partial^2\Psi(x,y,z,t)}{\partial z^2}=\frac 1{v^2}\frac{\partial^2\Psi(x,y,z,t)}{\partial t^2}[/math] w postaci harmonicznych fal stojących: [math]\Psi(x,y,t)=A\sin(k_xx+\delta_x)\sin(k_yy+\delta_y)\sin(\omega t +\phi)[/math].

Jeśli uwzględnimy warunki brzegowe — membrana jest zamocowana na końcach (co matematycznie oznacza, że dla dowolnej chwili czasu t spełnione są warunki [math]\Psi(x=0,y,t)=\Psi(x=a,y,t)=\Psi(x,y=0,t)=\Psi(x,y=b,t)= 0[/math] to otrzymamy, że składowe wektora falowego mogą przyjmować tylko następujące wartości:

[math]k_x=\frac{n\pi}a[/math],

[math]k_y=\frac{m\pi}b[/math].

gdzie n i m są liczbami całkowitymi. Stąd otrzymujemy, że długość wektora falowego, częstotliwość fali i jej długość przyjmują tylko następujące wartości:

[math]k_{n,m}=\pi\sqrt{\frac{n^2}{a^2}+\frac{m^2}{b^2}}[/math]

[math]f_{n,m}=\frac v 2\sqrt{\frac{n^2}{a^2}+\frac{m^2}{b^2}}[/math]

[math]\frac 1{\lambda_{n,m}}=\frac 12\sqrt{\frac{n^2}{a^2}+\frac{m^2}{b^2}} [/math]

Jeśli membrana byłaby kwadratowa [math](a=b)[/math] to:

W przypadku membrany kwadratowej tej samej częstotliwości odpowiadają różne rodzaje fal, np. [math]n=1\ \mathrm i\ m=2\ \mathrm{oraz}\ n=2\ \mathrm i\ m=1[/math].

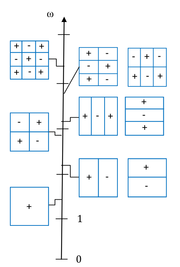
Na rysunku Figure 2 schematycznie pokazano rodzaje fal stojących w kwadratowej membranie zamocowanej na końcach.

Postacie fal stojących w kwadratowej membranie zamocowanej na końcach (przyjęto: [math]\nicefrac{\pi v}{a}[/math]).

O wiele bardziej skomplikowany matematycznie jest przypadek membrany kołowej. Klasyczne równanie falowe zapisujemy we współrzędnych cylindrycznych:

[math]\frac{\partial^2\Psi}{\partial\rho^2}+\frac 1\rho \frac{\partial\Psi}{\partial\rho}+\frac 1{\rho^2}\frac{\partial^2\Psi}{\partial\phi^2}=\frac{1}{v^2}\frac{\partial^2\Psi}{\partial t^2}[/math].

Poszukujemy rozwiązania w postaci fali stojącej: [math]\Psi(\rho,\phi,t)=R(\rho,\phi)\cos(\omega t+\delta)[/math]. Po podstawieniu do równania falowego i uwzględnieniu równości [math]\frac{\omega^2}{v^2}=k^2[/math] otrzymujemy równanie na funkcję [math]R(\rho,\phi)[/math]:

[math]\frac{\partial^2R}{\partial\rho^2}+\frac 1\rho \frac{\partial R}{\partial\rho}+\frac 1{\rho^2}\frac{\partial^2R}{\partial\phi^2}=-k^2R[/math]

Wprowadzając oznaczenie [math]x=k\rho[/math] oraz przyjmując [math]R(\rho,\phi)=X(x)\Phi(\phi)[/math] otrzymujemy dwa równania:

[math]\frac{\mathrm d^2\Phi}{\mathrm d\phi^2}=-m^2\Phi[/math]

[math]x^2 \frac{\mathrm d^2X}{\mathrm dx^2}+x\frac{\mathrm dX}{\mathrm dx} +(x^2-m^2) X=0[/math]

Rozwiązania pierwszego równania są następujące: [math]\Phi_1=\cos m\phi,\ \Phi_2=\sin m\phi[/math], natomiast drugie równanie nosi nazwę równania Bessela. Równanie to pojawia się dość często w fizyce. Jego rozwiązanie — funkcje Bessela (oznaczane [math]J_m(x)[/math]) są stablicowane.

Rozwiązania w postaci fal stojących membrany kołowej zamocowanej na końcach są więc następujące:

1. [math]m=0[/math], funkcja falowa jest postaci: [math]\Psi_{n0}(\vec r,t)=P_{n0}(\rho)\cos(\omega_{n0}t+\delta)[/math]. Funkcja ta ma pełną symetrię obrotową.
2. [math]m\neq 0[/math], dwie liniowo niezależne funkcje falowe:

   [math]\Psi^1_{nm}=P_{nm}(\rho)\cos(m\phi)\cos(\omega_{nm}t+\delta_1)[/math]

   [math]\Psi^2_{nm}=P_{nm}(\rho)\sin(m\phi)\cos(\omega_{nm}t+\delta_2)[/math]

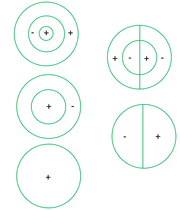
Na rysunku Figure 3 pokazano schematycznie kilka postaci fal stojących.

Przykładowe postacie fal stojących w membranie kołowej zamocowanej na końcach.