WnioskowanieStatystyczne/Prawdopodobienstwo

Wnioskowanie_Statystyczne_-_wykład

Definicje prawdopodobieństwa

Częstościowa definicja prawdopodobieństwa

Niech eksperyment [math]\Omega [/math] ma [math]N[/math] "równie prawdopodobnych" wyników [math]A_{i}[/math]:

[math] \Omega =A_{1},A_{2},...A_{N}. [/math]

Jeśli zdarzenie [math]E[/math] określone jest przez podzbiór przestrzeni [math]\Omega[/math] o liczebności [math]M[/math]

[math] E=A_{1}\cup A_{2}...\cup A_{M} [/math]

to prawdopodobieństwo zdarzenia [math]E[/math] określamy jako

[math] P(E)=\frac{M}{N}.[/math]

Aksjomatyczna definicja prawdopodobieństwa

Jak widać, w częstościowej definicji wykorzystane jest definiowane pojęcie (w odniesieniu do "równie prawdopodobnych" wyników), co z punktu widzenia teorii jest niewątpliwie poważnym defektem. Można go uniknąć, wprowadzając prawdopodobieństwo jako liczbę spełniającą po prostu poniższe aksjomaty (aksjomatyczna definicja prawdopodobieństwa):

[math] P(A)\geq 0 [/math]

[math] P(\Omega )=1 [/math]

jeśli A i B wykluczają się nawzajem, to

[math] P(A\cup B)=P(A)+P(B) [/math]

Oznaczmy symbolem [math]\overline{A}[/math] dopełnienie zdarzenia [math]A[/math] do przestrzeni [math]\Omega[/math]. Wtedy (1) i (2) implikują:

[math] 1=P(\Omega )=P(A\cup \overline{A})=P(A)+P(\overline{A}) [/math]

czyli

[math] \ 0\leq P(A)\leq 1 [/math]

(Ten wniosek bywa dołączany jako czwarty aksjomat.)

Ta definicja jest już formalnie poprawna, jednak nie dostarcza żadnego przepisu na sposób obliczania definiowanej wielkości, co uniemożliwia jej praktyczne zastosowanie. Z kolei różne od klasycznego, Bayesowskie podejście do statystyki określa prawdopodobieństwo jako miarę wiary w możliwość wystąpienia danego zdarzenia — jego obliczanie również bywa niełatwe.

Pojęcie prawdopodobieństwa leży u podstaw klasycznej teorii statystyki, stąd problemy z jego ścisłą definicją mogą rzucać cień na wiarę w jej spójność. Z drugiej strony, jak zauważa J.L. Simon:

(...) dyskusja ta przypomina kontrowersje wokół pojęcia czasu (czym czas naprawdę "jest"), które powstrzymywały postęp w fizyce, dopóki Einstein nie powiedział, że czas powinniśmy zdefiniować po prostu jako to, co odczytuje się z zegara.

Przykład

Spróbujmy określić prawdopodobieństwo zdarzenia, że poprowadzona w sposób przypadkowy cięciwa okręgu będzie miała długość większą od promienia.

Rozwiązanie:

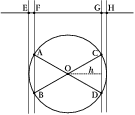
Jak "przypadkowo" poprowadzić cięciwę? Narysujmy dowolną prostą i wybierzmy na niej losowo punkt. Przez ten punkt prowadzimy prostopadłą, której punkty przecięcia z okręgiem będą wyznaczać cięciwy. Oczywiście nie wszystkie punkty na prostej dadzą prostopadłe, które będą miały w ogóle punkty wspólne z okręgiem — tylko punkty z odcinka E–H rys.%i 1. Z tych punktów graniczną cięciwę o długości równej promieniowi będzie wyznaczał punkt F, dla którego trójkąt AOB będzie równoboczny. Analogicznie z drugiej strony dla punktu G i trójkąta COD. Tak więc wszystkie punkty z odcinka EH będą generować cięciwy, a punkty z odcinka FG — cięciwy dłuższe od promienia. Prawdopodobieństwo "wylosowania" cięciwy dłuższej niż promień będzie równe stosunkowi długości odcinka FG do EH. Jeśli pamiętamy wzór na wysokość trójkąta równobocznego, łatwo znajdziemy jego wartość: [math]\frac{\sqrt{3}} 2[/math].

Jak poprowadzić przypadkowo cięciwę okręgu: sposób pierwszy.

Inne rozwiązanie:

Wybieramy losowo punkt wewnątrz okręgu, i prowadzimy przez niego prostą prostopadłą do promienia przechodzącego przez ten sam punkt. Jak widać z rys.%i 2, prosta ta wyznaczy cięciwę dłuższą niż promień, jeśli punkt będzie położony w odległości mniejszej niż [math]\frac{\sqrt{3}}{2}[/math] od środka. Wyznacza to wnętrze okręgu o promieniu [math]\frac{\sqrt{3}}{2}[/math], którego pole wyniesie [math]\frac{3\pi}{4}[/math] (przyjmujemy jednostkowy promień ,,dużego okręgu). Szukane prawdopodobieństwo jest stosunkiem tej wielkości do pola ,,dużego okręgu, czyli wynosi [math]\frac{3}{4}[/math].

Jak poprowadzić przypadkowo cięciwę okręgu: sposób drugi.

Jeszcze inne rozwiązanie:

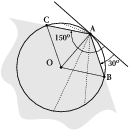
Wyznaczmy na okręgu punkt, z którego będziemy prowadzić cięciwy (punkt A na rys.%i 3). Parametrem określającym jednoznacznie cięciwę będzie kąt między styczną do okręgu w danym punkcie a jej kierunkiem, od [math]0^\circ[/math] do [math]180^\circ[/math]. Cięciwy o długości większej niż długość promienia będą wyznaczone przez kąty od [math]30^\circ[/math] do [math]150^\circ[/math] (trójkąty BOA i COA na rys.%i 3 są równoboczne). Stanowi to dwie trzecie zakresu kątów wyznaczających cięciwy, więc szukane prawdopodobieństwo wynosi [math]\frac{2}{3}[/math].

Jak poprowadzić przypadkowo cięciwę okręgu: sposób trzeci.

???

Co się nie zgadza? Przykład ten nie podważa bynajmniej idei geometrycznej interpretacji prawdopodobieństwa w ogóle; po prostu wynik zależy od przepisu na "przypadkowe" przeprowadzenie cięciwy — każde z rozwiązań zakłada losowanie według równomiernego rozkładu innego parametru (położenia punktu na prostej, położenia punktu wewnątrz okręgu, kąta). Można więc powiedzieć, że problem nie został ściśle sformułowany.

Prawdopodobieństwo warunkowe i zdarzenia niezależne

Zapis [math]P(A\mid B)[/math] oznacza prawdopodobieństwo zdarzenia [math]A[/math] liczone w sytuacji, gdy mamy pewność wystąpienia zdarzenia [math]B[/math]. Odpowiada to w pewnym sensie wystąpieniu obydwu zdarzeń ([math]A\cap B[/math]), jednak prawdopodobieństwo tej sytuacji należy obliczać inaczej niż [math]P(A\cap B[/math]).

Przyklad

Niech [math]A[/math] oznacza wyrzucenie szóstki, a [math]B[/math] — wyrzucenie parzystej liczby oczek w rzucie kostką. Wtedy [math]A\cap B[/math] oznacza wyrzucenie szóstki, [math]P(A\cap B)=\frac{1}{6}[/math]. Jednak jeśli bierzemy pod uwagę tylko te przypadki, w których wyrzucono parzystą liczbę oczek (2, 4 lub 6), to [math]P(A\mid B)=\frac{1}{3}[/math].

Rozważmy [math]P(A\mid\Omega)[/math]; dla dowolnego [math]A[/math] mamy

[math] P(A)=P(A\mid\Omega)=P(A\cap\Omega)[/math]

bo oczywiście [math]A\in\Omega[/math]. Rozbijając przestrzeń wszystkich możliwych zdarzeń [math]\Omega[/math] na część odpowiadającą zdarzeniu [math]B[/math] i pozostałą [math]\overline B[/math] ([math]\Omega=B\cup\overline{B}[/math]), dostajemy:

[math] P(A)=P(A\mid\Omega)=P\left(A\cap(B\cup\overline{B})\right)=P\left((A\cap B)\cup(A\cap\overline{B})\right)=P(A\cap B) + P(A\cap\overline{B}),[/math]

czyli prawdopodobieństwo zdarzenia [math]A[/math] jest równe sumie prawdopodobieństw zajścia [math]A[/math], jeśli zaszło również [math]B[/math], oraz prawdopodobieństwa zajścia [math]A[/math], jeśli [math]B[/math] nie zaszło. Jeśli wiemy, że zaszło zdarzenie [math]B[/math] (wszak liczymy [math]P(\cdot\mid B)[/math]), to drugi człon znika ([math]P(\overline{B})=0[/math]). Aby uzyskać wzór na [math]P(A\mid B)[/math], pozostały człon musimy podzielić przez [math]P(B)[/math] (aby dla [math]B=A[/math] było [math]P(A\mid A)=1[/math]):

[math] P(A\mid B)=\frac{P(A\cap B)}{P(B)} [/math]

Jeśli wystąpienie zdarzenia [math]B[/math] nie ma żadnego wpływu na prawdopodobieństwo wystąpienia zdarzenia [math]A[/math], czyli [math]P(A\mid B)=P(A)[/math], to mówimy, że zdarzenia [math]A[/math] i [math]B[/math] są niezależne. Z (%i 5) wynika, że dla zdarzeń niezależnych A i B [math] P(A\cap B)=P(A)P(B). [/math]

---