FizykaI FMiN/Dynamika inertials
Dynamika: układy nieinercjalne
Układ inercjalny
Sformułowana przez Newtona Zasada bezwładności
"Każde ciało trwa w swym stanie spoczynku lub ruchu prostoliniowego i jednostajnego, jeśli siły przyłożone nie zmuszajż ciała do zmiany tego stanu."
nie jest spełniony w dowolnym układzie odniesienia.
Szczególną klasę układów odniesienia, w których jest ona spełniona nazywamy układami inercjalnymi
Zasada bezwładności jest równoważna z postulatem itnienia układu inercjalnego.
W układzie inercjalnym ruch ciała jest jednoznacznie zadany przez działające na nie siły zewnętrzne (równanie ruchu)
- [math] m \; \frac{d^2 \vec{r}(t)}{dt^2} \; = \; \vec{F}(\vec{r}, \vec{v}, t) \; + \; \vec{F}_R [/math]
oraz warunki początkowe
- [math] \vec{r}(t_0)= \vec{r}_0 [/math]
- [math] \vec{v}(t_0)= \vec{v}_0 [/math]
Układy nieinercjalne
Opis ruchu
Przyjmijmy, że układ związany ze stolem laboratoryjnym jest układem inercjalnym.
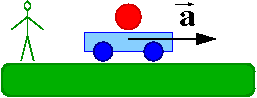
Na stole stoi wózek, a na nim spoczywa drugi ciało, które może się swobodnie poruszać (w doświadczeniu była to kulka). W pewnej chwili wózek zaczyna poruszać się z przyspieszenien [math]\vec{a}[/math] względem stołu.
Z punktu widzenia obserwatora związanego ze stołem kulka pozostaje w spoczynku. Wynika to z zasady bezwładności - siły działające na kulkę równoważą się
- [math]\vec{F}=0 \; \Leftrightarrow \; \vec{a}=0[/math]
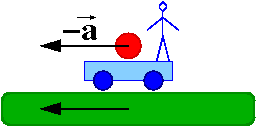
Z punktu widzenia obserwatora związanego z wózkiem kulka porusza się z przyspieszeniem [math]-\vec{a}[/math], mimo, że nie działają na nią żadne zewnętrzne siły.
Wynika z tego, że w układzie tym zasada bezwładności Newtona nie jest spełniona!
Układ ten nie jest więc układem inercjalnym.
Jeśli dwa układu odniesienia poruszają się względem siebie z przyspieszeniem to przynajmniej jeden z nich nie jest układem inercjalnym!
Prawa ruchu
Przyjmijmy, że układ O' porusza się z przyspieszeniem [math]\vec{a}_\circ[/math] względem układu inercjalnego O.
Zakładamy, że osie obu układów pozostają cały czas równoległe (brak obrotów).
Niech [math]\vec{r}_\circ(t)[/math] opisuje położenie układu O' w O.
Możemy z tego wyznaczyć przyspieszenie układu O' względem układu O:
- [math]\vec{a}_\circ = \frac{d^2 \vec{r}_\circ}{dt^2}[/math]
Ruch punktu materialnego mierzony w układach O
i O':
- [math] \vec{r} \; = \; \vec{r}\;' \; + \; \vec{r}_\circ [/math]
Przyspieszenie punktu materialnego mierzone w układach O i O':
- [math]\vec{a} \; = \; \vec{a}\;' \; + \; \vec{a}_\circ [/math]
Prawa ruchu w układzie inercjalnym O:
- [math] m \vec{a} \; = \; \vec{F}(\vec{r},\vec{v},t) \; + \; \vec{F}_R [/math]
Z tego wynika, że w układzie nieinercjalnym O':
- [math] m \vec{a}\;' \; = \; \vec{F}(\vec{r}\;',\vec{v}\;',t) \; + \; \vec{F}_R \; \; - \; m \vec{a}_\circ [/math]
Oznacza to, że w układzie nieinercjalnym musimy wprowadzić siłę pozorną zwaną siłą bezwładności:
- [math]\vec{F}_b \; = \; - m \vec{a}_\circ[/math]
Ruch poziomy
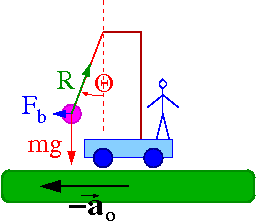
Rozważmy wahadło w układzie nieinercjalnym poruszającym się z przyspieszeniem [math]\vec{a}_\circ[/math] względem układu inercjalnego. Niech przyspieszenie to będzie skierowane poziomo.
Oprócz siły ciężkości [math]m\vec{g}[/math] i reakcji [math]\vec{R}[/math] w opicie ruchu wahadła musimy uwzględnić pozorną siłę bezwładności [math]\vec{F}_b = - m \vec{a}_\circ[/math]
Działanie sił bezwładności jest nierozróżnialne od siły grawitacji. Opis ruchu można uprościć wprowadzając efektywne przyspieszenie ziemskie:
- [math] \vec{g}\;' \; = \; \vec{g} - \vec{a}_\circ[/math]
Obserwujemy odchylenie położenia równowagi (kierunku "pionu", czyli efektywnego pola grawitacyjnego):
- [math] \tan \theta \; = \; \frac{a_\circ}{g} [/math]
oraz przyspieszenie drgań (wzrost wartości efektywnego przyspieszenie ziemskiego):
- [math] \omega'\;^2 \; = \; \frac{g'}{l} \; = \; \frac{\sqrt{g^2 + a^2}}{l} [/math]
Jeśli przyspieszenie układu [math]a_\circ \ll g[/math]
([math]\vec{a}_\circ \perp \vec{g}[/math])
obserwujemy tylko pozorną zmianę
kierunku działania siły ciężkości, natomiast
zmiana jej wartości jest znikoma.
Równia
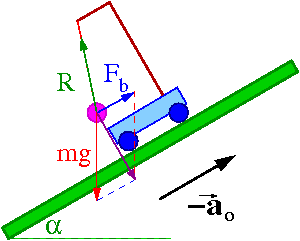
Rozważmy teraz wahadło w układzie nieinercjalnym związanym z wózkiem, który zsuwa się bez tarcia po równi pochyłej. Zaniedbując ruch obrotowy kół przyspieszenie wózka:
- [math] a_\circ \; = \; g \; \sin \alpha [/math]
W układzie związanym z wózkiem działająca na wahadło siła bezwładności jest równa co do wartości (lecz przeciwnie skierowana) równoległej składowej ciężaru.
Na wahadło działa więc pozorna siła ciężkości prostopadła do powierzchni równi.
- [math] g' \; = \; g_{\perp} \; = \; g \; \cos \alpha \; \lt \; g [/math]
Obserwujemy więc powolnienie drgań.
Spadek swobodny
W układzie odniesienia poruszającym się z przyspieszeniem [math]\vec{a}_\circ |\!| \vec{g}[/math] obserwujemy pozorną zmianę wartości przyspieszenie grawitacyjnego:
- [math] \vec{g}\;' \; = \; \vec{g} - \vec{a}_\circ[/math]
W układzie związanym z ciałem spadającym swobodnie [math]\vec{a}_\circ = \vec{g}[/math]
- [math] \vec{g}\;' \; = \; 0 [/math]
czyli obserwujemy stan nieważkości
W statkach kosmicznych stronauci nie dla tego znajdują się w stanie nieważkości, że siła ciężkości przestaje na nich działać. Znajdują się w nieinercjalnym układzie odniesienia, który porusza się z przyspieszeniem równym (lokalnemu) przyspieszeniu ziemskiemu (zakładając, że silniki rakietowe są wyłączone).
Układy obracające się
Układ inercjalny
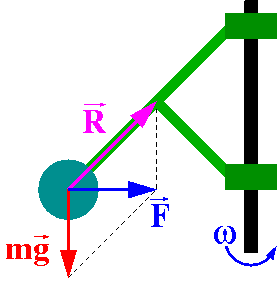
Rozważaliśmy już poprzednio ciała poruszające się po okręgu (przykłady:
regulator Watta, kulka w wirującej sferze). W układzie inercjalnym,
zgodnie z zasadami dynamiki Newtona, do utrzymania ciała w ruchu po
okręgu konieczna jest siła dośrodkowa.
W wymienionych przkładacj siła dośrodkowa jest tu wypadkową
siły reakcji i siły ciężkości (patrz rysunek):
- [math]\vec{F} \; = \; m \vec{g} \; + \; \vec{R}[/math]
Układ obracający się
Rozważmy powyższe przykłady we współobracającym się układzie odniesienia.
Niech układ O' obraca się z prędkością kątową [math]\vec{\omega}[/math] względem układu inercjalnego O. Dla uproszenia przyjmijmy, że początki obu układów pokrywają się.
Rozważmy ruch punktu materialnego spoczywającego w układzie O'. Z punktu widzenia obserwatora O ciało porusza się po okręgu i musi na nie dzialać siła dośrodkowa:
- [math] \vec{F} \; = \; - m \; \omega^2 \; \vec{r}_{\perp} [/math]
W układzie O' ciało pozostaje w spoczynku. Aby spełniona była zasada bezwładności działające na nie siły muszą się równoważyć. Musimy do opisu wprowadzić siłę bezwładności:
- [math] \vec{F}_b \; = \; + m \; \omega^2 \; \vec{r}_{\perp} [/math]
Siłę tą nazywamy siłą odśrodkową.
Siła odśrodkowa, tak jak siła bezwładności (w przypadku przyspieszenia liniowego) jest siłą pozorną, wynikającą z nieinercjalnego charakteru układu odniesienia. Pojawia się niezależnie od tego czy ciało w tym układzie spoczywa, czy też porusza się.
Nie wolno jej mylić z siłą dośrodkową, która konieczna jest do utrzymania ciała w ruchu po okręgu.
Siła odśrodkowa
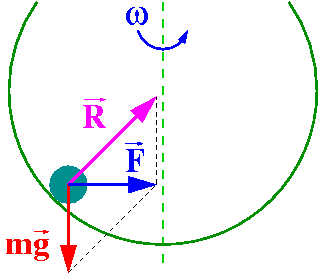
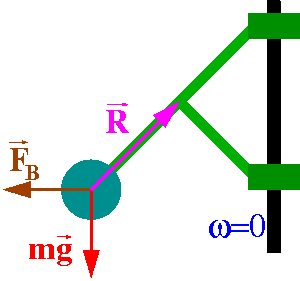
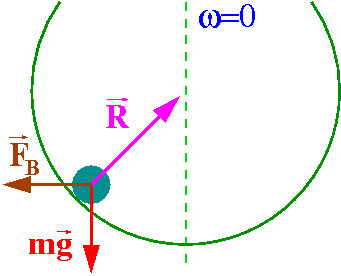
W rozważanych przykładach ciała spoczywają w układzie obracającym się:
 |
|
Siła odśrodkowa zapewnia równowagę sił w układzie obracającym się:
| [math] m \vec{g} \; + \; \vec{R} \; + \; \vec{F}_b \; = \; m \vec{a}\;' \; = \; 0 [/math] |
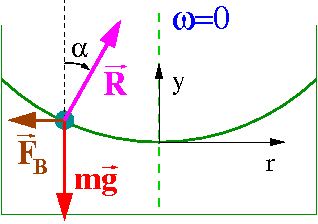
Innym przykładem jest też ciecz w wirującym naczyniu.
Powierzchnia cieczy przyjmuje kształt paraboliczny
Równowaga drobiny na powierzchni cieczy (rozważamy tylko składową równoległą do powierzchni cieczy):
- [math]m g \sin \alpha - m \omega^2 r \cos \alpha \; = \; 0 [/math]
Możemy z tego równania wyznaczyć pochodną funkcji opisującej kształt powierzchni cieczy:
- [math] \frac{dy}{dr} \; = \; \tan \alpha \; = \; \frac{\omega^2}{g} \; r [/math]
Całkując wyrażenie na pochodną otrzymujemy równanie paraboli:
- [math] y \; = \; \frac{\omega^2}{2g}\cdot r^2 + y_\circ [/math]
Ruch obrotowy Ziemi
Jak już wspomniano powyżej, układ związany z powierzchnią Ziemi (lub np. stołem laboratoryjnym). Nie jest ściśle inercjalny. Głównym powodem jest ruch obrotowy Ziemi z prędkością kątową:
- [math] \omega \; \approx \; \frac{2 \pi}{23^h \; 56^m \; 04^s} \; \approx \; 7.3 \cdot 10^{-5}\; \frac{1}{s} [/math]
W przypadku ciał nieruchomych względem powierzchni Ziemi siła odśrodkowa powoduje zmianę efektywnego przyspieszenia ziemskiego zwiazana z ruchem obrotowym Ziemi:
- [math] \Delta g \; = \; - \; \omega^2 r_\perp \; \cos \phi =
- \; \omega^2 r_Z \; \cos^2 \phi [/math]
- [math] \; \approx \; - 0.033 \frac{m}{s^2} \cdot \cos^2 \phi [/math]
gdzie [math]\phi[/math] - szerokość geograficzna.
Wyniki pomiarów:
miejsce [math]g[/math] biegun N 9.83216 [math]\frac{m}{s^2}[/math] Warszawa 9.81230 [math]\frac{m}{s^2}[/math] równik 9.78030 [math]\frac{m}{s^2}[/math]
Efekt jest większy od oczekiwanego ze względu na spłaszczenie Ziemi.
Siła Coriolisa
Spoczynek
Tak jak poprzenio rozważamy układ O', który obraca się z prędkością kątową [math]\vec{\omega}[/math] względem układu inercjalnego O.
Zastanówmy się teraz nad opisem ruchu punktu materialnego spoczywającego w układzie O. Wiemy więc, że na ciało nie działa żadna siła (albo działające siły równoważą się).
Z punktu widzenia obserwatora O' ciało porusza się po okręgu i musi na nie dzialać siła dośrodkowa:
- [math] \vec{F} \; = \; - m \; \omega^2 \; \vec{r}_{\perp} [/math]
W układzie O' działa tymczasem pozorna siła odśrodkowa:
- [math] \vec{F}_b \; = \; + m \; \omega^2 \; \vec{r}_{\perp} [/math]
Siła ta nie może powodować ruchu po okręgu bo ma zwrot przeciwny do siły dośrodkowej!
Aby "uratować" równania ruchu w układzie obracającym się musimy wprowadzić kolejną siłę:
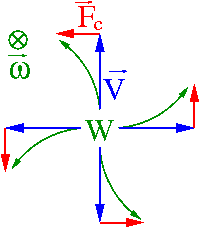
- [math] \vec{F}_c \; = \; - 2 \; m \; \omega^2 \; \vec{r}_{\perp} [/math]
Pojawia się uzasadnione pytanie, czy to w ogóle ma sens?
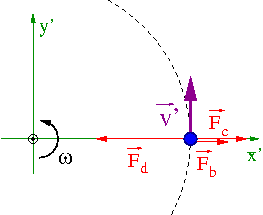
Ruch po okręgu
Rozważmy przypadek bardziej ogólny: punkt materialny poruszający się po okręgu w układzie inercjalnym O z prędkością [math]V[/math]. Do utrzymania ciała w tym ruchu potrzebne jest działanie siły dośrodkowej
- [math]F_d = m \frac{V^2}{r}[/math]
W układzie obracającym się O' prędkość punktu wynosi
- [math]V' = V - \omega \; r[/math]
Siła wypadkowa w O':
- [math] F'_d \; = \; m \frac{{V'}^2}{r} \; = \; m \frac{(V' + \omega r)^2}{r} - 2 m \omega V' - m \omega^2 r \; = \; F_d - F_c - F_b [/math]
Dodatkowa siła pozorna [math]\vec{F}_c[/math] (siła Coriolisa) konieczna jest do poprawnego opisania ruchu po okręgu w O'.
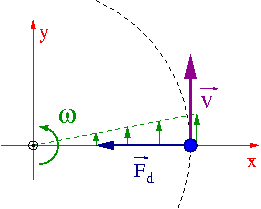
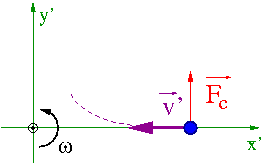
Ruch radialny
Rozważmy teraz punkt materialny poruszający się radialnie w układzie O'.
W inercjalnym układzie O zbliżający się do centrum układu punkt materialny zaczyna "wyprzedzać" punkty układu O', gdyż ich prędkość w ruchu obrotowym maleje...
Pozorna siła Coriolisa pojawia się w układzie obracającym się (nieinercjalnym), żeby opisać odchylenie od toru prostoliniowego...
Przypadek ogólny
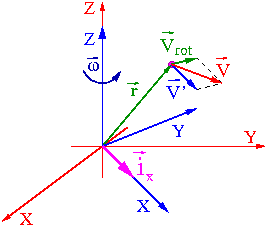
Układ O' obraca się z prędkością kątową [math]\vec{\omega}[/math] względem układu inercjalnego O.
Dodawanie prędkości możemy zapisać w postaci:
- [math] \vec{v} \; = \; \vec{v}\;' \; + \; \vec{v}_{rot} \; = \; \vec{v}\;' \; + \; \vec{\omega} \times \vec{r}\;' [/math]
Wynika z tego wzór na transformację przyspieszenie (z pochodnej iloczynu):
- [math] \vec{a} \; = \; \frac{d\vec{v}}{dt} \; = \; \frac{d\vec{v}\;'}{dt} \; + \; \frac{d\vec{\omega}}{dt} \times \vec{r}\;' \; + \; \vec{\omega} \times \frac{d\vec{r}\;'}{dt} [/math]
Kluczowe w tym momencie jest zauważenie, że pochodna wektora z układu O' ([math]\vec{r}\;'[/math] i [math]\vec{v}\;'[/math]; dla uproszczenia oznaczmy wektor przez )[math]\vec{o}'[/math] zmienia się przy zmianie układu odniesienia. Licząc pochodną w układzie O musimy dodatkowo uwzględnić fakt, że osie układu O' (względem których mierzony jest wektor [math]\vec{o}'[/math]) obracają się w układzie O. Związek między pochodnymi możena zapisać w postaci:
- [math] \frac{d \vec{o}\;' }{dt} \; = \; \frac{d \vec{o}\;'}{dt'} \; + \; \vec{\omega} \times \vec{o}\;' [/math]
gdzie przez [math] \frac{d}{dt}[/math] oznaczyliśmy symbolicznie pochodną w układzie O, a przez [math] \frac{d}{dt'}[/math] pochodną wyznaczaną w O'. Człon [math] \vec{\omega} \times \vec{o}\;' [/math] opisuje wkład związany z obrotem osi układu.
Uwzględniając powyższą zależność między pochodnymi otrzymujemy ogólny związek między przyspieszeniem ciała w układach O i O':
- [math] \vec{a} \; = \; \vec{a}\;' \; +\; \frac{d\vec{\omega}}{dt} \times \vec{r}\;' \; +\; \vec{\omega} \times ( \vec{\omega} \times \vec{r}\;' ) \; +\; 2 \cdot \vec{\omega} \times \vec{v}\;' [/math]
gdzie kolejne człony odpowiadają przyspieszeniu ciała w układzie O', ew. przyspieszeniu kątowemu układu O', przyspieszeniu dośrodkowemu i przyspieszeniu Coriolisa.
Równanie ruchu
W układzie inercjalnym O ogólne równanie ruchu ma postać:
- [math] m \vec{a} \; = \; \vec{F}(\vec{r},\vec{v},t) \; + \; \vec{F}_R [/math]
W obracającym się ze stałą prędkością kątową układzie nieinercjalnym O' otrzymaliśmy związek (patrz wzór na przyspieszenie powyżej):
- [math] m \vec{a}\;' \; = \; \vec{F}(\vec{r}\;',\vec{v}\;',t) \; + \; \vec{F}_R \; - \; m \; \vec{\omega} \times ( \vec{\omega} \times \vec{r}\;') \; - \; 2 \cdot m \; \vec{\omega} \times \vec{v}\;' [/math]
W układzie obracającym się wprowadzamy dwie pozorne siły bezwładności:
- siłę odśrodkową
- [math]\vec{F}_{o} = - m \; \vec{\omega} \times ( \vec{\omega} \times \vec{r}\;') = + m \; \omega^2 \; \vec{r}_{\perp}\;' [/math]
- siłę Coriolisa
- [math]\vec{F}_{c} = - 2 \cdot m \; \vec{\omega} \times \vec{v}\;'[/math]
Ruch obrotowy Ziemi
Siła Coriolisa pojawia się w szczególności gdy rozważamy ruch ciał w układzie związanym z powierzchnią ziemi.
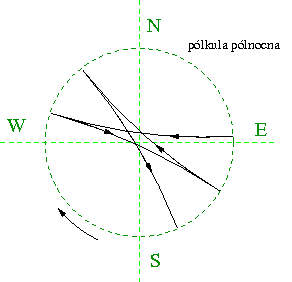
W przypadku spadku swobodnego z dużej wysokości odchyla tor ciała w kierunku wschodnim (zawsze! zarówno na półkuli północnej jak i południowej).
Dla przykładu, przy spadku z prędkością [math]v \approx 55[/math] m/s (dla uproszczenia przyjmijmy, że prędkość jest stała, np. w wyniku oporów ruchu):
- [math] a_c \; = \; 2 \; \omega \; v \; \cos \phi [/math]
- [math] \; \approx \; 0.008 \; \frac{m}{s^2}\cdot \cos \phi [/math]
Spadek z wysokości h=5.5 km
zajmie w tym przypadku[math]t = 100\; s[/math].
Końcowe odchylenie toru od pionu (ruch jednostajnie przyspieszony w
kierunku poziomym) wyniesie:
- [math] \Delta \; = \; \frac{a_c \; t^2}{2} \; \approx \; 40 \; m \cdot \cos \phi [/math]
w Warszawie około 25 m.
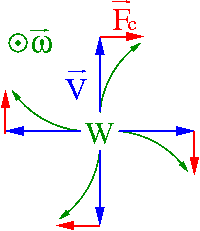
Wpływ siły Coriolisa jest wyraźnie widoczny gdy oglądamy prognozę pogody. To siła Coriolisa powoduje odchylenie prądów powietrza płynących od wyżu do niżu. Wiatry wiejące od wyżu zakręcają inaczej na półkuli północnej i południowej. Wiąże się to z inną oriętacją wektora prędkości obrotowej Ziemi.
- [math]\vec{F}_{c} = - 2 \cdot m \; \vec{\omega} \times \vec{v}\;'[/math]
- Półkula północna
- Wiatry zakręcają "w prawo", wyż "kręci się" zgodnie z ruchem wskazówek zegara
- Półkula południowa
- Wiatry zakręcają "w lewo", wyż "kręci się" przeciwnie do ruchu wskazówek zegara
Wahadło Foucault'a
Najbardziej spektakularnym efektem związanym z siłą Coriolisa jet tzw. Wahadło Foucault'a. Jest to zwykłe wahadło matematyczne w którym płaszczyzna drgań może się zmieniać (dwa stonie swobody), a opory ruchu są na tyle małe, że możemy obserwować wahania przez wiele godzin.
Dla obserwatora związanego z powierzchnią Ziemi płaszczyzna ruchu wahadła obraca się z prędkością kątową
- [math] \omega_1 \; = \; \omega \cdot \sin \phi [/math]
w Warszawie ([math]\phi = 52^\circ[/math]) obserwujemy obrót z prędkością kątową
- [math]\omega_1^{WAW} \approx 12^\circ /h[/math]