FizykaII NI/Ćwiczenia V
Zadanie 1
Potraktuj elektron jako kulę o promieniu [math]a[/math], na powierzchni której znajduje się ładunek. Znaleźć energię pola elektrycznego elektronu. Przyjmując, że energia ta jest równa energii spoczynkowej elektronu określ promień kuli (elektronu).
Zadanie 2
Oblicz energię potencjalną kuli naładowanej powierzchniowo, korzystając z definicji natężenia pola elektrycznego jako gradientu potencjału.
Zadanie 3
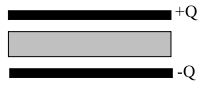
Dany jest kondensator płaski o polu powierzchni okładek [math]S = \unit{115}{ cm^2}[/math] i odległości między okładkami [math]d = \unit{1,24}{cm}[/math]. Do okładek przyłożono różnicę potencjałów [math]U_0 = \unit{85,5}{V}[/math]. Następnie odłączono źródło i między okładki wsunięto płytę o grubości [math]b = \unit{0,78}{ cm}[/math] i przenikalności dielektrycznej [math]\epsilon = 2,61[/math], jak pokazano na poniższym rysunku.
- Ile wynosi pojemność [math]C_0[/math] kondensatora przed włożeniem płyty dielektrycznej?
- Jaki ładunek swobodny znajduje się na okładkach?
- Ile wynosi natężenie pola elektrycznego [math]E_0[/math] w szczelinach między okładkami i płytą dielektryczną?
- Ile wynosi natężenie pola elektrycznego [math]E_1[/math] w płycie dielektrycznej?
- Ile wynosi różnica potencjałów [math]U[/math] między okładkami kondensatora po wsunięciu płyty?
- Ile wynosi pojemność kondensatora [math]C_1[/math] z płytą dielektryczną między okładkami?
Zadanie 4
Znaleźć pojemność kondensatora płaskiego o odległości między okładkami [math]d[/math], powierzchni okładek [math]S[/math], długości okładek [math]l[/math], miedzy które na głębokość [math]x[/math] wsunięty jest dielektryk o przenikalności [math]\epsilon[/math]. Policz siłę wciągającą dielektryk do kondensatora przy różnicy potencjałów na okładkach kondensatora [math]U[/math].