Pochodne 2

Pochodna funkcji odwrotnej

Niech będzie dana w przedziale [math][a,b]\;[/math] funkcja różniczkowalna i różnowartościowa [math]y=f(x)\;[/math]. Wiadomo, że istnieje wówczas funkcja odwrotna [math]f^{-1}\;[/math] (którą oznaczymy tu [math]g\;[/math] : [math]x=g(y)\;[/math] ), ciągła w przedziale [math][f(a), f(b)]\;[/math] (lub [math][f(b), f(a)]\;[/math] — zależnie od tego, czy [math]f\;[/math] jest rosnąca czy malejąca). Pokażemy, że w tym przedziale funkcja [math]g\;[/math] też jest różniczkowalna, a przy okazji wyprowadzimy wzór na pochodną funkcji odwrotnej. Mianowicie mamy

Twierdzenie

Jeśli [math]f(x)=y\;[/math] tzn. [math]x=g(y)\;[/math], to

[math] g'(y)\equiv \frac{d g(y)}{d y} = \frac{1}{f'(x)} =\frac{1}{\frac{d f(x)}{d x}}. \;[/math]

przy założeniu że [math]f'(x)\ne 0\;[/math].

Dowód

Przy zadanym [math]x\;[/math] weźmy [math]k= f(x+h)-f(x)\;[/math]. Mamy więc [math]f(x+h)=y+k\;[/math], tzn. [math]x+h=g(y+k)\;[/math], skąd [math]h=g(y+k)-g(y)\;[/math]. Możemy więc traktować [math]h\;[/math] jako funkcję [math]k\;[/math]. Ze względu na ciągłość funkcji [math]g\;[/math], mamy [math]\lim_{h \to 0} h(k)=0\;[/math], a ponadto dla [math]k\ne 0\;[/math] mamy [math]h\ne 0\;[/math], ponieważ funkcja [math]g\;[/math] jest różnowartościowa. Mamy więc:

[math] g'(y)=\lim_{k\to 0}\frac{g(y+k)-g(y)}{k} =\lim_{h \to 0}\frac{h}{f(x+h)-f(x)} =\frac{1}{f'(x)}. \;[/math]

Przy drugiej równości powyżej korzystaliśmy z faktu, iż dla funkcji ciągłych [math]F(x)\;[/math], [math]G(y)\;[/math] mamy: Jeśli [math]y_0 = F(x_0)\;[/math], to [math]\lim_{x\to x_0} G(F(x)) = \displaystyle\mathop{\lim}_{y \to y_0} G(y)\;[/math].

CBDO

Uwaga

Twierdzenie powyższe ma ilustrację/interpretację geometryczną. Rozpatrzmy krzywą daną równaniem [math]y=f(x)\;[/math]. Poprowadźmy w jakimś punkcie [math](x_0,y_0\;[/math] (tu [math]y_0=f(x_0)\;[/math]) styczną do tej krzywej i znaczmy przez [math]\alpha\;[/math] kąt utworzony przez styczną z osią [math]OX\;[/math], a przez [math]\beta;[/math] — kąt utworzony przez styczną z osią [math]OY\;[/math]. Oczywiście [math]\alpha=\frac{\pi}{2}-\beta\;[/math]. Wówczas [math]\tg\; \beta = \ctg\; \alpha\;[/math] czyli [math]\tg\;\beta=\frac{1}{\tg\;\alpha}\;[/math] — zgodnie z wzorem (1). Za pomocą powyższego twierdzenia policzymy pochodne kolejnych funkcji elementarnych.

Twierdzenie

[math](e^x)'=e^x\;[/math] i, ogólniej, [math](a^x)'= a^x \ln a\;[/math].

Dowód

Weźmy [math]y=f(x)=e^x\;[/math] ; wtedy [math]x=f^{-1}(y)\equiv g(y)=\ln y\;[/math]. Mamy: [math]g'(y)=\frac{1}{y}=\frac{1}{e^x}=\frac{1}{f'(x)}\;[/math], a ostatnia równość to właśnie [math]f'(x)=(e^x)' =e^x\;[/math].

W ogólniejszym przypadku [math](a^x)'\;[/math], bierzemy [math]y=f(x)=a^x\;[/math], a dla funkcji odwrotnej [math]x=g(y)=\log_a y\;[/math]. Pamiętamy, że [math]g'(y)=\frac{1}{y\ln a}=\frac{1}{f'(x)}\Longrightarrow f'(x)=a^x\ln a\;[/math].

CBDO

Twierdzenie

1. [math](\arcsin x)'=\frac{1}{\sqrt{1-x^2}}\;[/math]
2. [math](\arccos x)'=-\frac{1}{\sqrt{1-x^2}}\;[/math].

Dowód

1. Weźmy [math]y=f(x)=\arcsin x\;[/math] i wtedy [math]x=g(y)=\sin\; y\;[/math]. Mamy: [math]g'(y)=\cos\; y =\sqrt{1-\sin\;^2 y}=\sqrt{1-x^2}=\frac{1}{f'(x)}\;[/math], (znak pierwiastka to plus, bo [math]x\in[-\frac{\pi}{2},+\frac{\pi}{2}]\;[/math] ), a ostatnia równość to [math]f'(x)=(\arcsin x)'= \frac{1}{\sqrt{1-x^2}}\;[/math].
2. Rozważania są analogiczne: [math]y=f(x)=\arccos x\;[/math], [math]x=g(y)= \cos\; y\;[/math] ; jedyna różnica jest w znaku, bo [math]g'(y)=-\sin\; y\;[/math] i dalej jak w a), z wynikiem końcowym [math](\arccos x)'=-\frac{1}{\sqrt{1-x^2}}\;[/math].

CBDO

Twierdzenie

[math](arctg x)' = \frac{1}{1+x^2}\;[/math].

Dowód

Dla [math]y=f(x)=arctg x\;[/math] jest [math]x=g(y)=\tg\; y\;[/math], [math]g'(y)=\frac{1}{\cos\;^2 y}\;[/math] ; stąd [math]f'(x)=\cos\;^2 y=\frac{1}{1+\tg\;^2 y}=\frac{1}{1+(\tg\;(arctg(x))^2}= \frac{1}{1+x^2}\;[/math].

Ekstrema funkcji. Twierdzenie Rolle'a

Maksimum i minimum

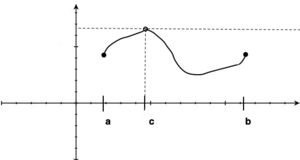
Niech funkcja [math]f\;[/math] będzie określona w otoczeniu punktu [math]a\;[/math] (tzn. w jakimś przedziale otwartym, zawierającym [math]a\;[/math] ). Jeśli istnieje takie [math]\delta\gt 0\;[/math], że

[math] \forall_{h: |h|\lt \delta}: f(a+h)\leq f(a), \;[/math]

to mówimy, że funkcja [math]f(x)\;[/math] ma maksimum w punkcie [math]a\;[/math]. Jeśli zaś przy analogicznych założeniach mamy nierówność:

[math] f(a+h)\geq f(a), \;[/math]

to mówimy, że funkcja [math]f(x)\;[/math] ma minimum w punkcie [math]a\;[/math].

Innymi słowy, w punkcie [math]a\;[/math] występuje maksimum (minimum), jeśli istnieje takie otoczenie [math]U\;[/math] punktu [math]a\;[/math], że [math]f(a)\;[/math] jest największą (najmniejszą) liczbą w zbiorze wartości, jakie funkcja [math]f\;[/math] przyjmuje na [math]U\;[/math].

Jeśli we wzorach (2) i (3) zastąpić znaki [math]\geq\;[/math] ([math]\leq\;[/math] ) przez [math]\gt \;[/math] ([math]\lt \;[/math] ), to mamy do czynienia z maksimum (minimum) właściwym.

Przykłady

1. Funkcja [math]x^2\;[/math] posiada minimum w punkcie [math]x=0\;[/math] ;
2. funkcja [math]\cos\; x\;[/math] posiada maksima w punktach [math]2 k \pi\;[/math], [math]k\in \mathbb Z \; \;[/math] oraz minima w punktach [math](2k+1)\pi\;[/math], [math]k\in \mathbb Z \; \;[/math].
3. funkcja [math]|x|\;[/math] posiada minimum w [math]x=0\;[/math].

Esktrema

Maksima i minima obejmujemy wspólną nazwą ekstremów funkcji [math]f\;[/math]. Z pojęciem ekstremum ściśle jest związane (ale różne) pojęcie kresów wartości funkcji na zbiorze. Ekstrema są pojęciami lokalnymi: Aby stwierdzić, czy funkcja posiada ekstremum w danym punkcie [math]a\;[/math], wystarczy znać wartości funkcji w dowolnie małym otoczeniu punktu [math]a\;[/math]. Natomiast wyznaczenie kresów zbioru wartości funkcji na zbiorze [math]X\;[/math] wymaga znajomości funkcji na całym [math]X\;[/math].

Z definicji maksimum wynika natychmiast

Twierdzenie

Jeśli funkcja [math]f\;[/math] określona w przedziale [math][a,b]\;[/math] osiąga kres górny w punkcie [math]c\;[/math] należącym do wnętrza tego przedziału (tzn. [math]a\lt c\lt b\;[/math] ), to funkcja posiada maksimum w [math]c\;[/math]. (analogicznie dla kresu dolnego i minimum).

CBDO

Kresy

Jeśli okaże się, że kres górny funkcji jest osiągany w jednym z końców przedziału [math][a,b]\;[/math] (np. w [math]a\;[/math] ), to nie mówimy, iż w tym punkcie funkcja posiada maksimum, ponieważ funkcja nie jest określona w otoczeniu [math]a\;[/math]. Np. funkcja [math]y=x\;[/math] na zbiorze [math]X=[0,1]\;[/math] posiada kres górny równy 1; nie nazywamy go jednak maksimum.

Twierdzenie

Jeśli funkcja [math]f\;[/math] jest różniczkowalna w punkcie [math]c\;[/math] i posiada w tym punkcie ekstremum, to [math]f'(c)=0\;[/math].

Dowód

Załóżmy, że [math]f\;[/math] posiada w punkcie [math]c\;[/math] maksimum (jeśli minimum, to rozumowanie jest analogiczne). Weźmy więc takie [math]\delta\gt 0\;[/math], aby dla dowolnego [math]h\;[/math] takiego, że[math]|h|\lt \delta\;[/math], zachodziła nierówność [math]f(c+h)-f(c)\leq 0\;[/math]. Dzieląc przez [math]h\;[/math], otrzymujemy

[math]\frac{f(c+h)-f(c)}{h}\leq 0\;\;\;[/math] dla [math]h\gt 0, \;\;\;\frac{f(c+h)-f(c)}{h}\geq 0\;\;\;[/math] dla [math]\;\;\;h\lt 0. \;[/math]

Ponieważ z założenia istnieje pochodna [math]f'(c)\;[/math], to

[math] f'_+(c)=f'_-(c)=f'(c). \;[/math]

Z poprzednich nierówności wynika jednak, że [math]f'_+(c)\leq 0\leq f'_-(c)\;[/math]. Musi więc być

[math] f'_+(c)=0=f'_-(c),\;\;\mbox{co znaczy, ze}\;f'(c)=0. \;[/math]

CBDO

Uwaga

Twierdzenie odwrotne nie zachodzi: Równość [math]f'(c)=0\;[/math] może być spełniona, mimo iż funkcja [math]f\;[/math] nie posiada ekstremum w [math]c\;[/math]. Jest tak np. dla funkcji [math]f(x)=x^3\;[/math] w punkcie [math]x=0\;[/math].

Punkt krytyczny

Jeśli funkcja jest różniczkowalna w [math]x=a\;[/math] i [math]f'(a)=0\;[/math], to punkt [math]x=a\;[/math] nazywamy punktem krytycznym funkcji [math]f\;[/math].

Uwaga

Istnienie ekstremum funkcji różniczkowalnej w punkcie [math]c\;[/math] oznacza, że styczna do krzywej [math]y=f(x)\;[/math] w punkcie [math](c,f(c)\;[/math] jest równoległa do osi [math]OX\;[/math] (z możliwością, że się z tą osią pokrywa).

Twierdzenie (Rolle'a)

Niech funkcja [math]f\;[/math] będzie ciągła w przedziale domkniętym [math][a,b]\;[/math] i różniczkowalna wewnątrz tego przedziału. Jeśli [math]f(a)=f(b)\;[/math], to istnieje takie [math]c\;[/math], że [math]a\lt c\lt b\;[/math] oraz [math]f'(c)=0\;[/math].

Jeżeli funkcja jest ciągła na przedziale domkniętym [a,b] i f(a)=f(b) to istnieje taki punkt c, że [math]f'(c)=0[/math] dla [math] c \in ]a,b[[/math]

Dowód

Jeśli funkcja [math]f\;[/math] jest stała, to [math]\forall_{x\in[a,b]} f'(x)=0\;[/math]. Można wtedy wziąć dowolny [math]x\in]a,b[\;[/math] i teza tw. Rolle'a będzie spełniona.

Załóżmy więc, że funkcja [math]f\;[/math] nie jest stała; np. niech przyjmuje wartości większe od [math]f(a)\;[/math]. Oznaczając przez [math]M\;[/math] kres górny zbioru wartości funkcji na przedziale [math][a,b]\;[/math], mamy: [math]M\gt f(a)\;[/math]. Zatem, z tw. Weierstrassa, istnieje takie [math]c\in[a,b]\;[/math], że [math]f(c)=M\;[/math]. Przy tym [math]a\ne c\ne b\;[/math], ponieważ z założenia [math]f(a)=f(b)\;[/math] ; zatem [math]a\lt c\lt b\;[/math]. To znaczy, że funkcja [math]f\;[/math] osiąga kres górny w punkcjie [math]c\;[/math] położonym wewnątrz przedziału [math][a,b]\;[/math]. Zgodnie z twierdzeniem niedawno udowodnionym funkcja [math]f\;[/math] posiada w punkcie [math]c\;[/math] maksimum, co z kolei implikuje (pamiętając o różniczkowalności [math]f\;[/math] wewnątrz przedziału), że [math]f'(c)=0\;[/math].

CBDO

Uwaga

Twierdzenie Rolle'a można sformułować w następujący sposób:

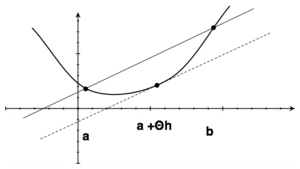
Jeśli [math]f(x)=f(x+h)\;[/math], to istnieje takie [math]\theta: 0\lt \theta\lt 1\;[/math], że

[math] f'(x+\theta h)=0. [/math]

przy tych samych założeniach, tzn. funkcja [math]f\;[/math] ma być różniczkowalna wewnątrz przedziału [math][x,x+h]\;[/math] (lub [math][x+h,x]\;[/math], jeśli [math]h\lt 0\;[/math] ; nie zakładamy tu, że [math]h\gt 0\;[/math] lecz jedynie że [math]h\ne 0\;[/math] ) i ciągła w [math]x\;[/math] oraz [math]x+h\;[/math].

Twierdzenie Lagrange'a i Cauchy'ego

Twierdzenie (Lagrange'a)

Załóżmy (podobnie jak w tw. Rolle'a), że funkcja [math]f\;[/math] jest ciągła w przedziale [math][a,b]\;[/math] i różniczkowalna wewnątrz tego przedziału. Zachodzi wówczas wzór

[math] \frac{f(b)-f(a)}{b-a}=f'(a+\theta h), \;[/math]

Twierdzenie Lagrange'a[math]f'(a+\theta h)=\frac{f(b)-f(a)}{b-a}[/math]

gdzie [math]h=b-a\;[/math] oraz [math]\theta\in]0,1[\;[/math].

Uwaga

Wzór ten nazywany jest też wzorem Lagrange'a na wartość średnią, lub twierdzeniem o przyrostach skończonych. Widać, że szczególnym przypadkiem (gdy [math]f(a)=f(b)\;[/math] ) jest tw. Rolle'a. Okazuje się, że dowód tw. Lagrange'a można sprowadzić do tw. Rolle'a.

Dowód

Weźmy mianowicie funkcję [math] g(x)=f(a)-f(x)+(x-a)\frac{f(b)-f(a)}{b-a} \;[/math] i ponadto [math]g(x)\;[/math] jest ciągła na [math][a,b]\;[/math] i różniczkowalna w [math]]a,b[\;[/math] ; jej pochodna jest

[math] g'(x)=-f'(x)+\frac{f(b)-f(a)}{b-a} \;[/math]

Ponadto [math]g(b)=0=g(a)\;[/math], zatem [math]g(x)\;[/math] spełnia założenia tw. Rolle'a. Skoro tak, to pochodna [math]g'(x)\;[/math] znika w pewnym punkcie między [math]a\;[/math] i [math]b\;[/math]. Możemy to wypowiedzieć tak, że istnieje takie [math]\theta: 0\lt \theta\lt 1\;[/math], że

[math] g'(a+\theta h)=0\;\;\;{\rm tzn.}\;\;\;0=-f'(a+\theta h)+\frac{f(b)-f(a)}{b-a}, \;[/math]

czyli zachodzi wzór z tezy tw. Lagrange'a.

CBDO

Uwaga

W sposób podobny, jak wzór (4) przy tw. Rolle'a, można tezę tw. Lagrange'a sformułować w następujący sposób:

Dla funkcji [math]f\;[/math] różniczkowalnej wewnątrz przedziału [math][x,x+h]\;[/math] i ciągłej na [math][x,x+h]\;[/math] (to dla [math]h\gt 0\;[/math] ; dla [math]h\lt 0\;[/math] jest to przedział [math][x+h,x]\;[/math] ) istnieje takie [math]\theta: 0\lt \theta\lt 1\;[/math], że

[math] f(x+h)=f(x)+f'(x+\theta h) \cdot h. \;[/math]

Wnioski wypływające z twierdzenia Lagrange'a

Z tw. Lagrange'a wypływają dwa wnioski, bardzo ważne dla rachunku całkowego:

Twierdzenie

Jeśli [math]\forall_{x\in ]a,b[}\;[/math] zachodzi [math]f'(x)=0\;[/math], to funkcja w tym przedziale jest stała.

Dowód

Na mocy udowodnionego dopiero co wzoru (6), mamy bowiem dla każdego [math]x\;[/math] i [math]h\;[/math]: [math]f(x)=f(x+h)\;[/math], co oznacza, że [math]f(x)=\;[/math] const.

CBDO

Twierdzenie

Jeśli [math]\forall_{x\in ]a,b[}\;[/math] zachodzi [math]f'(x)=g'(x)\;[/math], to [math]f(x)=g(x)+\;[/math] const.

Dowód

Mamy: [math](f(x)-g(x))'= f'(x)-g'(x)=0\;[/math], czyli funkcja [math]f(x)-g(x)\;[/math] ma pochodną równą zeru. Na mocy dopiero co udowodnionego twierdzenia znaczy to, że [math]f(x)-g(x)\;[/math] jest stała, tzn. [math]f(x)=g(x)+\;[/math] const.

CBDO

Twierdzenie (Cauchy'ego; (czasem z przydomkiem: O wartości średniej))

Jeśli funkcje [math]f\;[/math] i [math]g\;[/math] są ciągłe na przedziale [math][a,b]\;[/math] i różniczkowalne wewnątrz oraz jeśli [math]\forall_{x\in ]a,b[}\;[/math] jest [math]g'(x)\ne 0\;[/math], to istnieje takie [math]\theta\in]0,1[\;[/math], że

[math] \frac{f(b)-f(a)}{g(b)-g(a)} = \frac{f'(a+\theta h)}{g'(a+\theta h)}, \;[/math]

gdzie [math]h=b-a\;[/math].

Przed dowodem

Uwaga

Twierdzenie Lagrange'a otrzymuje się z tw. Cauchy'ego, jeśli podstawić [math]g(x)=x\;[/math]. Okazuje się, że także tw. Cauchy'ego wynika z tw. Lagrange'a, ale tu trzeba zaargumentować następująco:

Dowód

Weżmy funkcję

[math] G(x)= f(a)-f(x) + (g(x)-g(a)) \frac{f(b)-f(a)}{g(b)-g(a)} \;[/math]

(mianownik [math]g(b)-g(a)\;[/math] jest różny od zera ze względu na założenie, że wszędzie w przedziale [math]]a,b[\;[/math] mamy [math]g'(x)\ne 0\;[/math] i tw. Rolle'a).

Funkcja [math]G(x)\;[/math] spełnia założenia tw. Rolle'a: Jest różniczkowalna i ciągła jak trzeba, oraz [math]G(a)=0=G(b)\;[/math]. Pochodna funkcji [math]G(x)\;[/math] jest

[math] G'(x)=-f'(x) + g'(x) \frac{f(b)-f(a)}{g(b)-g(a)}; \;[/math]

zatem (z tw. Rolle'a) istnieje takie [math]\theta\in]a,b[\;[/math], że [math]G'(a+\theta h)=0\;[/math]. Podstawiając [math]x=a+\theta h\;[/math] we wzorze (8), otrzymujemy (7).

Analogicznie do sposobu, w jaki tw. Rolle'a i Lagrange'a były wyrażane wzorami (4) i (6), można tw. Cauchy'ego sformułować tak: Istnieje [math]\theta\in]0,1[\;[/math] takie, że

[math] \frac{f(x+h)-f(x)}{g(x+h)-g(x)}=\frac{f'(x+\theta h)}{g'(x+\theta h)}. \;[/math]

Uwaga

W powyższym wzorze [math]\theta\;[/math] jest TO SAMO w liczniku i mianowniku.

Różniczkowanie funkcji złożonych

Niech [math]y=f(x)\;[/math], [math]z=g(y)\;[/math], przy tym funkcja [math]g\;[/math] jest określona na zbiorze wartości funkcji [math]f\;[/math] ; ponadto niech [math]f\;[/math] i [math]g\;[/math] będą różniczkowalne, a pochodna [math]g'\;[/math] niech będzie ciągła. Następujący wzór wyraża pochodną funkcji złożonej [math]g(f(x))\;[/math] przez pochodne [math]f'\;[/math] i [math]g'\;[/math].

Twierdzenie

[math](g(f(x)))' = f'(x) \cdot g'(f(x)), \;\;\;[/math] tzn. [math]\frac{d (g(f(x))}{d x} = \frac{d f(x)}{d x} \cdot \left[\frac{d g(y)}{d y}\right]_{y=f(x)}. \;[/math]

Dowód

Przy danych [math]x\;[/math] i [math]h\ne 0\;[/math] weźmy [math]k=f(x+h)-f(x)\;[/math], tzn. [math]f(x+h)=y+k\;[/math]. Zastosujmy teraz wzór Lagrange'a na wartość średnią w wersji (6) do funkcji [math]g\;[/math] ; otrzymamy

[math] \frac{g(f(x+h)) - g(f(x))}{h}=\frac{g(y+k)-g(y)}{h}=g'(y+\theta k)\cdot \frac{k}{h}=g'(y+\theta k) \cdot \frac{f(x+h)-f(x)}{h}. [/math]

dla pewnego [math]\theta \in ]0,1[\;[/math] (pamiętajmy, że [math]\theta\;[/math] jest pewną funkcją [math]h\;[/math] ). Co stanie się z powyższym wyrażeniem, gdy weźmiemy jego granicę przy [math]h\to 0\;[/math]? Otóż ze względu na ciągłość funkcji [math]g\;[/math], mamy [math]\displaystyle\mathop{\lim}_{h\to 0} k =0\;[/math], a ponieważ [math]0\lt \theta\lt 1\;[/math], to również [math] \displaystyle\mathop{\lim}_{h\to 0} \theta k =0\;[/math]. Skoro tak, to [math]\displaystyle\mathop{\lim}_{h\to 0} (y+\theta k)=y\;[/math], co — w połączeniu z ciągłością funkcji [math]g'\;[/math] — daje

[math] \displaystyle\mathop{\lim}_{h\to 0} g'(y+\theta k)= g'(y) =g'(f(x)). \;[/math]

Mamy więc:

[math] \frac{d g(f(x))}{d x}=\displaystyle\mathop{\lim}_{h\to 0} \frac{g(f(x+h))-g(f(x))}{h} =\displaystyle\mathop{\lim}_{h\to 0} g'(y+\theta k) \displaystyle\mathop{\lim}_{h\to 0}\frac{f(x+h)-f(x)}{h}=g'(f(x))\cdot f'(x). \;[/math]

Przykłady

1. [math](\sin\;^2 x)'\;[/math] na dwa sposoby:
   1. [math](\sin^2(x))'=(\sin(x) \sin(x))'=\sin(x) \cos(x) + \cos(x) \sin(x) = 2\sin(x) \cos(x) \;[/math]
   2. (różniczkowanie funkcji złożonej) [math](\sin^2(x))' = (\sin(x))' 2(\sin(x)) = 2\sin(x) \cos(x)\;[/math]
2. [math](e^{\sin(x)})'=(\sin(x))'e^{\sin(x)} = \cos(x) e^{\sin(x)}\;[/math]
3. Udowodnimy teraz anonsowany wcześniej wzór [math] (x^a)'=a x^{a-1}\;\;\;{\rm dla}\;\;\; a\in\mathbb R \; . \;[/math]

   Dow. Napiszmy [math]x^a\;[/math] w postaci: [math]x^a=e^{a\ln x}\;[/math] i ze wzoru na pochodną funkcji złożonej

   [math] (x^a)'=(e^{a\ln x})' =\frac{d e^{a\ln x}}{d x}=\frac{d a \ln x}{d x} \cdot \left. \frac{d e^y}{d y}\right|_{y=a\ln x}=a\frac{1}{x} e^y|_{y=a\ln x}= a x^{-1}x^a =a x^{a-1} [/math] CBDO

Niejednokrotnie trzeba kilkakrotnie zastosować twierdzenie o pochodnej funkcji złożonej. Mamy np. pochodną funkcji trzykrotnie złożonej:

[math] h(g(f(x)))' = f'(x) \cdot g'(f(x)) \cdot h'(g(f(x)) \;[/math]

Sztuczka mnemoteczniczna

Wzór powyższy można zapamiętać np. w następujący sposób:

Oznaczmy: [math]y=f(x)\;[/math], [math]z=g(y)\;[/math], [math]w=h(z)\;[/math], oraz [math]W(x)=h(g(f(x)))\;[/math]. Można wtedy napisać

[math] \frac{d W}{d x}= \frac{d w}{d z}\cdot \frac{d z}{d y }\cdot\frac{d y }{d x}, \;[/math]

pamiętając,w jakich punktach są liczone wszystkie pochodne.

W powyższym wzorze pochodne zachowują się jak ułamki. Ale UWAGA! Jest to zbieżność przypadkowa; inne pochodne (zwł. cząstkowe) już siętak nie zachowują!

Uwaga — wzór na pochodną funkcji odwrotnej

ze wzoru na pochodną funkcji złożonej: [math]f^{-1}(f(x))=x,\;[/math] biorąc pochodną: [math]f'(x)(f^{-1})' (f(x))'=1\;[/math] i [math](f^{-1})'(f(x))=\frac{1}{f'(x)}[/math] lub [math](f^{-1})'(x)=\frac{1}{f'(f^{-1}(x))}\;[/math]

Związek między znakiem pochodnej a monotonicznością funkcji

Z tw. Lagrange'a wynika następujący związek pomiędzy znakiem pochodnej a tym, czy funkcja rośnie, czy maleje.

Twierdzenie *

Jeśli [math]\forall_{x\in [a,b]}\;[/math] zachodzi nierówność [math]f'(x)\gt 0\;[/math], to funkcja [math]f\;[/math] jest w tym przedziale ściśle rosnąca. Jeśli mamy [math]f'(x)\lt 0\;[/math], to funkcja [math]f\;[/math] jest ściśle malejąca.

Dowód

Ze wzoru (6) mamy, dla [math]h\gt 0\;[/math] : [math]f(x+h)\gt f(x)\;[/math] jeśli w przedziale [math][x,x+h]\;[/math] pochodna jest stale dodatnia, bądź [math]f(x+h)\lt f(x)\;[/math], jeśli pochodna jest stale ujemna. Czyli funkcja jest ściśle rosnąca w pierwszym przypadku, a ściśle malejąca w drugim.

CBDO

Uwaga

Jeśli założyć, że zachodzi nierówność nieostra [math]f'(x)\geq 0\;[/math] ([math]f'(x)\leq 0\;[/math] ), to w tezie mamy, że funkcja jest rosnąca (malejąca).

Zachodzi również twierdzenie odwrotne do powyższego:

Twierdzenie

Jeśli funkcja [math]f\;[/math] jest różniczkowalna w punkcie [math]c\;[/math] i rośnie (maleje) w jakimś przedziale [math]]a,b[\;[/math] zawierającym ten punkt, to [math]f'(c)\geq 0\;[/math] (odpowiednio [math]f'(c)\leq 0\;[/math] ).

Dowód

Jeśli [math]f\;[/math] rośnie, to dla [math]h\gt 0\;[/math] mamy

[math] f(c+h)-f(c)\geq 0 \Longrightarrow \frac{f(c+h)-f(c)}{h}\geq 0 \;[/math]

i przechodząc do granicy [math]\displaystyle\mathop{\lim}_{h\to 0}\;[/math] otrzymujemy [math]f'(c)\geq 0\;[/math].

Jeśli funkcja [math]f\;[/math] maleje, to rozumowanie jest analogiczne.

CBDO

Z tw. *(https://brain.fuw.edu.pl/edu/Matematyka:Pochodne1#Twierdzenie_.2A) wynika

Twierdzenie (wynikające z tw. *)

Jeśli [math]f'(c)\gt 0\;[/math] i pochodna [math]f'(x)\;[/math] jest ciągła w punkcie [math]c\;[/math], to funkcja [math]f\;[/math] jest ściśle rosnąca w pewnym otoczeniu punktu [math]c\;[/math].

Analogicznie: Jeśli [math]f'(c)\lt 0\;[/math] i pochodna [math]f'(x)\;[/math] jest ciągła w punkcie [math]c\;[/math],to funkcja [math]f\;[/math] jest ściśle malejąca w pewnym otoczeniu punktu [math]c\;[/math].

Dowód

Ponieważ funkcja [math]f'(x)\;[/math] jest ciągła w [math]c\;[/math], to nierówność [math]f'(c)\gt 0\;[/math] mówi, że w pewnym otoczeniu punktu [math]c\;[/math] funkcja [math]f'(x)\;[/math] jest dodatnia: [math]\exists_{\delta\gt 0}: \forall_{h\lt \delta}: f'(c+h)\gt 0\;[/math]. Znaczy to, że pochodna [math]f'\;[/math] jest dodatnia [math]\forall_x: c-h\lt x\lt c+h\;[/math]. Na mocy https://brain.fuw.edu.pl/edu/Matematyka:Pochodne1#Twierdzenie_.2A, funkcja [math]f\;[/math] jest rosnąca w tym przedziale.

CBDO

Uwaga

Powyższe twierdzenie można przeformułować w następujący sposób:

1. Jeśli [math]f'(c)\ne 0\;[/math], to (przy założeniu ciągłości pochodnej) funkcja [math]f\;[/math] jest różnowartościowa w pewnym otoczeniu punktu [math]c\;[/math], tzn. dla [math]]c-\delta, c+\delta[\;[/math] ([math]\delta \gt 0\;[/math] ). Skoro tak, to funkcja [math]f\;[/math] posiada w tym przedziale funkcję odwrotną [math]x=g(y)\;[/math], czyli równanie: [math]y=f(x)\;[/math] posiada w tym przedziale dokładnie jedno rozwiązanie..
2. Jak wiemy, pochodna tejże funkcji odwrotnej [math]g'(y)\;[/math] jest odwrotnością pochodnej funkcji [math]f'(x)\;[/math].
3. Powyższe fakty: Przy założeniu [math]f'(c)\ne 0\;[/math] istnieje w otoczeniu punktu [math]f(c) \;[/math] funkcja odwrotna, lub że równanie: [math]y=f(x)\;[/math] ma dokładnie jedno rozwiązanie w otoczeniu punktu [math]c\;[/math] — przenoszą się na wyższe wymiary, tzn. zachodzą dla odwzorowań [math]\mathbb R \; ^n \to \mathbb R \; ^n\;[/math]. Oczywiście konieczne jest stosowne uogólnienie pojęć. Będzie o tym mowa w semestrze II.

Wyrażenia nieoznaczone i reguła de l'Hospitala

Często zdarza się konieczność obliczania granic postaci następującej: [math]\displaystyle\mathop{\lim}_{x\to a} \frac{f(x)}{g(x)}, \;\;\;\; {\rm gdzie}\;\;\; f(a)=0=g(a).\;[/math] Wyrażenia tego rodzaju noszą nazwę wyrażeń nieoznaczonych typu [math]\frac{0}{0}\;[/math].

Twierdzenie

Jeśli funkcje [math]f\;[/math] i [math]g\;[/math] są ciągłe w przedziale domkniętym [math][a,b]\;[/math] i są różniczkowalne wewnątrz tego przedziału i jeśli [math]f(a)=0=g(a)\;[/math], to

[math] \displaystyle\mathop{\lim}_{x\to a^+} \frac{f(x)}{g(x)} =\displaystyle\mathop{\lim}_{x\to a^+} \frac{f'(x)}{g'(x)} \;[/math]

przy założeniu, że ta ostatnia granica istnieje.

Dowód

Kluczem do dowodu jest twierdzenie Cauchy'ego o wartości średniej.

Oznaczmy: [math]x=a+h\;[/math]. Należy dowieść, że [math] \lim_{h\to 0^+} \frac{f(a+h)}{g(a+h)} =\lim_{h \to 0^+} \frac{f'(a+h)}{g'(a+h)}.\;[/math] Ale: Równości: [math]f(a)=0=g(a)\;[/math] i wzór Cauchy'ego (7) dają:

[math] \frac{f(a+h)}{g(a+h)}= \frac{f(a+h)-f(a)}{g(a+h)-g(a)}=\frac{f'(a+\theta h)}{g'(a+\theta h)} \;[/math]

dla pewnego [math]\theta\in]0,1[\;[/math].

Oznaczmy [math]F(x)=\frac{f'(x)}{g'(x)}\;[/math]. Z założenia [math]\displaystyle\mathop{\lim}_{h\to 0^+} F(a+h)\;[/math] istnieje.

Ponieważ zaś [math]\displaystyle\mathop{\lim}_{h\to 0^+} x= 0 \;[/math], to też [math]\displaystyle\mathop{\lim}_{h\to 0^+} x\theta= 0 \;[/math] i, co za tym idzie, [math]\displaystyle\mathop{\lim}_{x\to 0^+} F(a+\theta h)\;[/math] też istnieje i jest równe [math]\displaystyle\mathop{\lim}_{x\to 0^+} F(a+ h)\;[/math]; mamy więc

[math] \displaystyle\mathop{\lim}_{x\to 0^+} \frac{f'(x+\theta h)}{g'(x+\theta h)} = \displaystyle\mathop{\lim}_{x\to 0^+} \frac{f'(x+h)}{g'(x+h)} \;[/math]

skąd otrzymujemy wzór (de l'Hospitala).

CBDO

Analogiczne twierdzenie mamy w przypadku granicy lewostronnej.

Wzór de l'Hospitala

W przypadku, gdy pochodne [math]f'\;[/math] i [math]g'\;[/math] są ciągłe w punkcie [math]a\;[/math], a ponadto [math]g'(a)\ne 0\;[/math], ze wzoru (10) (plus jego odpowiednika dla granicy lewostronnej) natychmiast wynika wzór de l'Hospitala:

[math] \displaystyle\mathop{\lim}_{x\to a} \frac{f(x)}{g(x)} = \frac{f'(a)}{g'(a)} \;[/math]

Uwaga

Po prawej stronie powyższego wzoru nie ma granicy!

Analogiczne wzory mamy w przypadku granic jednostronnych i pochodnych jednostronnych.

Przykład

[math] \begin{matrix} \displaystyle\mathop{\lim}_{x\to 0}\frac{\ln(1+x)}{x}= \displaystyle\mathop{\lim}_{x\to 0}\frac{\frac{1}{1+x}}{1}=1\\ \displaystyle\mathop{\lim}_{x\to 0}\frac{e^x-1}{x} = \displaystyle\mathop{\lim}_{x\to 0}\frac{e^x}{1}=1 \end{matrix} [/math]

Uwaga

Jeśli zdarzy się, że po prawej stronie wyrażenia (12) mamy [math]f'(a)=g'(a)=0\;[/math], to tegoż wzoru nie daje się stosować. Ale można postępować rekurencyjnie! tzn. badać wyższe pochodne.

Uwaga

Powyższe twierdzenia dotyczyły wyrażeń typu [math]\frac{0}{0}\;[/math]. Przez sztuczki z zamianą zmiennych i inne, można też liczyć inne wyrażenia nieoznaczone: [math]\frac{\infty}{\infty}\;[/math] ; [math]\infty-\infty\;[/math] ; [math]1^\infty\;[/math] ; [math]0^0\;[/math] ; [math]\infty^0\;[/math].