Reprezentacje czas-częstość
AS/ Reprezentacje czas-częstość
Transformata Wignera daje jako pierwotny wynik estymatę gęstości energii sygnału w przestrzeni czas-częstość; jej pełny obraz zawiera rzędu [math]N^2[/math] wartości — dla sygnału o długości [math]N[/math] punktów mamy w każdym punkcie [math]N/2[/math] częstości. Z kolei przekształcenia Fouriera czy falkowe opisują sygnał w kategorii współczynników określających "dopasowanie" sygnału do konkretnych funkcji: [math]e^{i\omega t}[/math], [math]g(t)e^{i\omega t}[/math] czy [math]\psi(\frac{t-u}s)[/math]. Liczba tych funkcji, których iloczyn z sygnałem będziemy traktować jako jego reprezentację, ustalamy właściwie dowolnie, ale zwykle jest ona bliższa rozmiarowi sygnału [math]N[/math] niż [math]N^2[/math]. W szczególnym przypadku bazy ortogonalnej, którą można stworzyć z funkcji [math]e^{i\omega t}[/math] lub falek [math]\psi(\frac{t-u}s)[/math], będzie ich dokładnie [math]N[/math].
Z tych współczynników możemy również utworzyć mapę gęstości energii sygnału w przestrzeni czas-częstość. Każdy iloczyn określa zawartość energii sygnału w pewnym przedziale czasu i częstości. Ze względu na zasadę nieoznaczoności, iloczyn tych przedziałów ("pole") nie może być dowolnie mały. Dla spektrogramu będą to jednolite przedziały o rozmiarach wyznaczonych przez szerokość okna [math]g(t)[/math]. Z kolei w przypadku transformacji falkowej wzrost częstości funkcji związany jest ze zmianą skali [math]s[/math], czyli "rozciąganiem" [math]\psi[/math], dlatego funkcje o niższej częstości będą zajmowały większy przedział czasu.
Okazuje się, że tworzone w ten sposób estymaty gęstości energii są równoważne pewnym sposobom uśredniania transformaty Wignera.
Która z tych metod jest najlepsza? Przede wszystkim musimy ustalić, co w tym miejscu znaczy "lepszy". Mamy do czynienia z reprezentacjami sygnału w postaci iloczynów z ustalonymi zestawami funkcji; najlepsza będzie taka reprezentacja, dla której większość z tych iloczynów jest bliska zeru. Dlaczego? Przede wszystkim oznacza to, że najważniejsze (lub raczej najsilniejsze) cechy sygnału udało się wyrazić z pomocą niewielu znanych funkcji, których iloczyny z sygnałem są istotnie różne od zera. Tak zwięzły opis sygnału odkrywa zwykle jego podstawowe cechy i ułatwia dalszą analizę. Poza poznaniem głównych cech badanego sygnału, wymiernym celem jest często kompresja.
Jeśli funkcje używane do analizy sygnału tworzą bazę ortogonalną, jak w przypadku transformaty Fouriera czy niektórych falek, to reprezentacj w takiej bazie zawiera dokładnie ilość informacji potrzebną do odtworzenia sygnału. Jeśli ilość funkcji wybranych do reprezentacji jest większa niż wymiar bazy, to mamy do czynienia z redundancją, ale odtworzenie sygnału z wartości iloczynów jest zwykle również możliwe. Tak więc jeśli zapiszemy tylko wartości większych iloczynów, to odtworzony z nich sygnał powinien być podobny do oryginału — jest to kompresja stratna, stosowana np. w popularnych formatach mp3 czy jpeg.
Problem wyboru reprezentacji pozostaje otwarty:
- transformata Fouriera opisuje zwięźle sygnały stacjonarne, w których dominuje niewielka ilość częstości (sinusoidalnych),
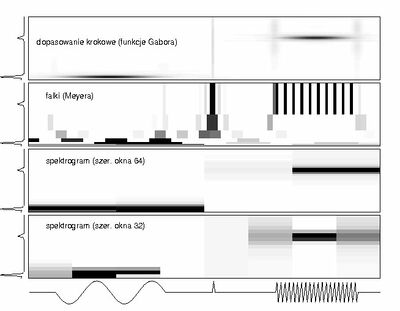
- w krótkoczasowej transformacie Fouriera trudno odgadnąć dla nieznanego sygnału optymalną szerokośc okna (por. dolne wykresy na rys. %i 1),
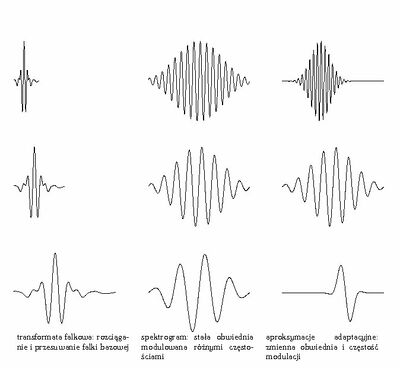
- w reprezentacji falkowej (a z różnych falek możemy konstruować różne reprezentacje) zwięźle opiszemy krótkie struktury przejściowe (ang. transients ), ale np. długi sinus będzie dawał duże wartości iloczynów z wieloma falkami (rys. %i 1),
- i tak dalej[math]\ldots[/math].
Dla każdego sygnału zwięzłą reprezentację możemy uzyskać wyrażając go w innym zestawie funkcji. A gdyby tak dopasować reprezentację do sygnału, wybierając odpowiednie funkcje z ogromnego (względem rozmiaru bazy, czyli redundantnego) zestawu? To podejście opisane jest w rozdziale o Matching Pursuit