TI/Metody numeryczne
Spis treści
Wprowadzenie
Jak już wiemy, aby móc zastosować komputer do rozwiązywania różnorodnych zagadnień musimy mu dokładnie przestawić plan działania — program. Program piszemy w oparciu o algorytm, który opisuje sposób rozwiązania danego problemu. Ten sposób musimy znaleźć sami, ale często możemy wykorzystać fakt, że podobne problemy ktoś już kiedyś rozwiązał. Uwaga ta dotyczy w szczególności całej gamy zagadnień obliczeniowych; algorytmy rozwiązywania typowych problemów znane są w literaturze właśnie jako metody numeryczne. Jest to też osobna dziedzina wiedzy: wiele problemów można rozwiązywać na kilka sposobów, próbuje się więc odpowiedzieć kiedy warto zastosować który sposób, który z nich jest najszybszy lub najdokładniejszy.
W tym rozdziale zaprezentujemy kilka przykładów problemów oraz wybrane sposoby ich rozwiązania. Oczywiście programy rozwiązujące te zagadnienia można znaleźć w gotowych bibliotekach i pakietach oprogramowania. Tutaj raczej skupimy się nie na wyniku, ale na sposobie jego otrzymania.
Precyzja obliczeń
Rozwinięcie dziesiętne ułamka
Zastanówmy się nad sposobem liczenia rozwinięcia dziesiętnego ułamka, na przykład 1/7. Gdy użyjemy do tego celu operatora dzielenia np. w Pythonie, otrzymamy wynik podobny do przedstawionego poniżej:
- >>> 1./7.
- 0.14285714285714285
Sprawa wydaje się prosta, widzimy, że mamy do czynienia z ułamkiem dziesiętnym okresowym 0,(142857). Ale jeśli przyjdzie nam policzyć:
- >>> 1./113.
- 0.0088495575221238937
to nie wiemy, czy widzimy cały okres ułamka, czy nie. Co możemy w tej sytuacji zrobić? Znamy ze szkoły algorytm dzielenia liczb, który pozwala policzyć dowolnie wiele cyfr rozwinięcia dziesiętnego. Jest to właśnie metoda numeryczna, której używamy nawet bez komputera. Musimy tylko zapisać ten algorytm (w uproszczonej wersji przedstawiony poniżej) w postaci programu komputerowego.
- policz c = a // b;
- zapisz c jako kolejną cyfrę wyniku;
- jeśli a < b to niech a = a * 10; w przeciwnym razie niech a = a % b * 10;
- jeśli nie zebraliśmy pożądanej ilości cyfr to idź do punktu 1.
Co się stanie, gdy w którymś momencie a będzie równe zero?
Zadania
Napisz program znajdujący zadaną (np. 100) liczbę cyfr rozwinięcia dziesiętnego ułamka. Znajdź okres rozwinięcia dziesiętnego ułamka 1/1245.
Oblicz wartość π (czyli tytułową ludolfinę) korzystając ze wzorów
- [math] \frac{\pi }{4} = \operatorname{arc\,tg\,}{1} [/math]
oraz
- [math] \operatorname{arc\,tg\,}{x} = \sum _{n=0}^{\infty } (-1)^n \frac{x^{2n+1}}{2n+1} = x - \frac{x^3}{3} + \frac{x^5}{5} - \frac{x^7}{7} + \cdots [/math]
z dokładnością ε = 10−20. Jak ocenić ile wyrazów ciągu należy policzyć, aby uzyskać zadaną dokładność?
Porównaj swój wynik z rozwinięciami ułamków: [math]\frac{22}{7}[/math], [math]\frac{335}{113}[/math], [math]\frac{104348}{33215}[/math].
Porównaj wynik z wartością z biblioteki cmath lub z tym wynikiem.
Oblicz wartość [math]\pi [/math], korzystając ze wzoru z poprzedniego zadania i zależności:
- [math] \frac{\pi }{4} = 4\, \operatorname{arc\,tg\,}\frac{1}{5} - \operatorname{arc\,tg\,}\frac{1}{239} [/math]
z dokładnością ε = 10−20.
Uwaga: Tutaj w liczniku każdego wyrazu szeregu nie stoi już jedynka. Ponieważ liczymy funkcję od argumentu ułamkowego, efektywnie zwiększa się za każdym razem wartość mianownika każdego wyrazu.
Oblicz z dokładnością ε = 10−20 sumę szeregu
- [math] a_n = \frac{1}{n^2}\text{.} [/math]
Oblicz z dokładnością ε = 10−20 wartość funkcji sin(0,5) korzystając z rozwinięcia w szereg:
- [math] \sin x = x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+...=\sum _{n=0}^\infty \frac{(-1)^{n}x^{2n+1}}{(2n+1)!} [/math]
Pewne zagadnienia algebry liniowej
Rozwiązywanie układu równań liniowych — metoda eliminacji Gaussa
Metoda eliminacja Gaussa to ładna nazwa na odejmowanie liniowych równań parami, aż do uzyskania formy w której z lewej strony mamy tylko jedną zmienną.
Rozważmy następujący układ równań, który chcemy rozwiązać:
Przepiszmy go w postaci macierzowej:
Metoda będzie polegała na odejmowaniu równań od siebie tak, aby uzyskać postać trójkątną. Ponieważ odejmujemy jednocześnie obie strony równań, połączmy macierze w jedną, wygodną do przekształceń. Mamy wtedy
Odejmujemy pierwszy wiersz od pozostałych, mnożąc elementy pierwszego wiersza tak, żeby w pierwszej kolumnie otrzymać zero dla wszystkich następnych wierszy. Po takiej operacji układ wygląda tak:
Zostawiamy pierwszy wiersz i przechodzimy do drugiego. Powtarzamy odejmowanie tak, aby w drugiej kolumnie uzyskać same zera (poza drugim wierszem). Dla większych macierzy postępujemy podobnie dla wszystkich kolejnych wierszy. Otrzymujemy:
Numeryczna stabilność algorytmu
Numeryczna stabilność algorytmu (odporność na błędy w wyniku w momencie występowania w macierzy jednocześnie małych i dużych liczb), poprawia się, jeśli do naszego algorytmu dołożymy zamianę wierszy. Jako wiersz do zamiany z [math]i[/math]-tym wierszem wybieramy wiersz [math]i[/math] lub wiersz leżący poniżej o największym elemencie w [math]i[/math]-tej kolumnie.
Cały algorytm wygląda więc tak (niech [math]N[/math] będzie liczbą równań)
for [math]i[/math] = 0, 1, …, N−1:
- biorąc pod uwagę wiersze [math]i[/math], …, N−1 znajdź numer [math]i_{\text{max}}[/math] wiersza o największym współczynniku w kolumnie [math]i[/math]
- zamień wiersze [math]i[/math] i [math]i_{\text{max}}[/math],
- podziel nowy wiersz [math]i[/math] przez [math]M_{ii}[/math],
- odejmij* nowy wiersz [math]i[/math] od wierszy i+1, …, N−1.
* Wiersz do odjęcia powinien zostać przemnożony przez element [math]M_{ki}[/math] z kolumny [math]i[/math] każdego z tych wierszy, tak by wyzerować ten element [math]M_{ki}[/math]. Zwróć uwagę na to, że [math]M_{ki}[/math] zmienia się w trakcie odejmowania, i wartość mnożnika trzeba zachować w zmiennej tymczasowej.
Po przekształceniu otrzymanej macierzy do postaci trójkątnej (dzieląc każdy wiersz przez element na przekątnej) w macierzy występują:
- zera poniżej przekątnej;
- jedynki na przekątnej;
- rozmaite wartości w górnym trójkącie.
- [math] \left[ \begin{matrix} 1 & \frac{1}{2} & -\frac{1}{2} \\ & 1 & 1 \\ & & 1 \end{matrix} \left| \begin{matrix} 4 \\ 2 \\ -1 \end{matrix}\right. \right] [/math]
Aby uzyskać rozwiązanie oryginalnego układu równań należy wyzerować górny trójkąt macierzy. Zaczynamy od ostatniego wiersza (który ma już pożądaną formę) i odejmujemy go od pozostałych mnożąc tak, aby przy odejmowaniu wyzerował się element w ostatniej kolumnie każdego wiersza powyżej ostatniego. Powtarzamy tę operację dla wszystkich wierszy aż do pierwszego.
for [math]i[/math] = N−1, …, 0:
- for [math]j[/math] = N−1, …, i+1:
- odejmij wiersz i+1 od wiersza [math]i[/math], tak by wyzerować element [math]M_{ij}[/math]
Proszę zwrócić uwagę, że w trakcie powyższego przekształcenia, przez
cały czas, wiersze o numerach większych od [math]i[/math] mają tylko jeden
element niezerowy wsród elementów leżących w kolumnach 0, …, N−1.
Wracając do powyższego przykładu
I w końcu
Czyli mamy rozwiązanie układu:
- [math] \left\{ \begin{matrix} x&=&2\\y&=&3\\z&=&-1 \end{matrix} \right. [/math]
Napisz funkcję rozwiązującą układ równań liniowych metodą eliminacji Gaussa z zamianą wierszy.
Znajdowanie macierzy odwrotnej
Powyższy algorytm można też wykorzystać do tego, by znaleźć macierz odwrotną. Z prawej strony macierzy „połączonej” należy wstawić macierz jednostkową
- [math] \left[ \begin{matrix} 2 & 1 & -1 \\ -3 & -1 & +2 \\ -2 & +1 & +2 \end{matrix} \left| \begin{matrix} 1 & & \\ & 1 & \\ & & 1 \end{matrix} \right.\right] [/math]
a następnie dokonywać przekształcenia w identyczny sposób jak powyżej. W momencie kiedy z lewej strony uzyskuje się macierz jednostkową, to z prawej strony uzyskuje się macierz odwrotną.
Napisz funkcję znajdującą macierz odwrotną.
Znajdowanie miejsc zerowych funkcji
W rozdziale tym zapoznamy się z prostymi algorytmami znajdowania miejsc zerowych funkcji ciągłych lub rozwiązania równań z jedną niewiadomą czyli znajdowania jego pierwiastków. Obie te operacje są sobie równoważne, gdyż znalezienie miejsca zerowego funkcji f(x) odpowiada rozwiązaniu równania f(x) = 0. Metody opisane poniżej są szczególnie istotne w przypadku funkcji nieliniowych, gdy znalezienie pierwiastków równania metodami analitycznymi jest poważnie utrudnione.
Metoda bisekcji (równego podziału)
Szukamy pierwiastków funkcji w zadanym obszarze. Korzystamy z twierdzenia:
Jeżeli funkcja f(x) jest
ciągła i ma na końcach przedziału domkniętego wartości różnych znaków,
to wewnątrz tego przedziału istnieje co najmniej jeden pierwiastek
równania [math]f(x)=0[/math] (tw. Bolzano-Cauchy'ego).
Rozważmy naszą funkcję ciągłą f. Stwierdzenie „co najmniej jeden pierwiastek” oznacza, że wybierając przedział [a;b], w którym będziemy poszukiwać pierwiastka, musimy się upewnić, że jest on tam tylko jeden. Jeśli tego nie zrobimy, nie będziemy wiedzieli, do którego z pierwiastków procedura będzie zdążać, jeśli w ogóle algorytm będzie w tym przypadku zbieżny. Zauważmy, że warunek ten odpowiada warunkowi stałości znaku pierwszej pochodnej w zadanym przedziale.
Procedura bisekcji jest iteracyjna i polega na znalezieniu środka xs przedziału [math][a;b][/math] oraz sprawdzeniu, czy pierwiastek znajduje się w lewej czy w prawej połowie tego przedziału. Następnie wybieramy nowy przedział biorąc za jeden z końców znaleziony właśnie środek xs, a za drugi taki z końców a lub b oryginalnego przedziału, aby funkcja miała na nowych końcach wartości przeciwnych znaków. Procedurę kończymy po osiągnięciu zadanej dokładności, gdy wartość funkcji w znalezionym punkcie lub różnica pomiędzy dwoma końcami przedziału nie przekracza [math]\epsilon[/math].
Napisz program rozwiązujący zadane równanie metodą bisekcji. Znajdź rozwiązania równań:
- cos(x) = tg(x) dla x ∈ [0, π/2);
- sin(x) = ln(x) − 1;
- x7 − 3x5 − 2x + 8 = 0 dla x ∈ [−2, −1], x ∈ [1, 2] oraz dla x ∈ [35, 40];
z dokładnością 10−5. Czy w każdym z zastosowanych przedziałów spełnione są założenia metody?
Metoda Newtona
Metoda ta również jest iteracyjna, i, podobnie jak poprzednio, wymaga znalezienia przedziału, dla którego funkcja ma na jego końcach różne wartości oraz stałą pierwszą pochodną wewnątrz przedziału. Dodatkowo wymagamy stałości drugiej pochodnej, czyli funkcja nie może mieć w tym przedziale punktu przegięcia.
Stosując metodę Newtona powinniśmy znać również pochodną naszej funkcji. Wybieramy punkt startowy na brzegu przedziału i wyznaczamy współrzędne prostej stycznej do naszej funkcji w tym punkcie. Punkt przecięcia tej stycznej z osią OX jest naszym przybliżonym rozwiązaniem. Jeśli wartość funkcji w tym punkcie nie jest dostatecznie bliska zera (<ε), to punkt ten wybieramy jako nowy punkt startowy i powtarzamy obliczenia.
Napisz program rozwiązujący zadane równanie metodą Newtona. Rozwiąż te same równania metodą Newtona i metodą bisekcji. Porównaj liczbę zastosowanych iteracji dla zadanej dokładności.
Pierwiastkowanie metodą Isaaca Newtona
Można pokazać, że kolejne iteracje w metodzie Newtona mogą być opisane wzorem
- [math]x_{n+1}=x_n-\frac{f(x_n)}{f^\prime(x_n)}[/math]
Jeżeli rozwiązujemy równanie [math]x^k=a[/math], to naszą funkcją jest [math]f(x)=x^k-a[/math] i otrzymujemy
Czyli metodą tą możemy wyliczyć pierwiastek danej liczby a stopnia k. Uwaga: słowo „pierwiastek” ma tu inne znaczenie niż w poprzednim rozdziale. Teraz [math]a[/math] to liczba pierwiastkowana, [math]x_n[/math] to wartość „poprzednia” pierwiastka, a xn+1 to wartość „ulepszona”.
W szczególności, dla [math]k=2[/math],
Korzystając ze wzoru %i 9 napisz funkcję liczącą [math]\sqrt{a}[/math].
Korzystając ze wzoru %i 8 napisz funkcję liczącą [math]\sqrt[n]{a}[/math].
Interpolacja
Interpolacja wielomianowa
W praktyce doświadczalnej często zachodzi potrzeba analizy wyników zebranych podczas eksperymentu. Podstawowym krokiem analizy jest zbadanie, jaka zależność opisuje nasze wyniki, czy pasują one do przyjętej hipotezy. W tym celu niezwykle użyteczne jest sporządzenie wykresu i próba dopasowania zakładanej zależności funkcyjnej do posiadanych danych. W najprostszym przypadku poszukujemy zależności liniowej, czyli poszukujemy takiej prostej, która najlepiej opisuje nasze wyniki. Oczywiście możemy dopasowywać nie tylko prostą, ale praktycznie każdą funkcję opisaną zestawem modyfikowalnych parametrów.
Próba opisu zależności funkcyjnej danych, gdy znane są wartości tylko w niektórych punktach nosi nazwę:
- interpolacji, gdy staramy się oszacować wartości funkcji pomiędzy posiadanymi punktami;
- ekstrapolacji, gdy staramy się oszacować wartości funkcji na zewnątrz obszaru obejmowanego przez posiadane przez nas punkty.
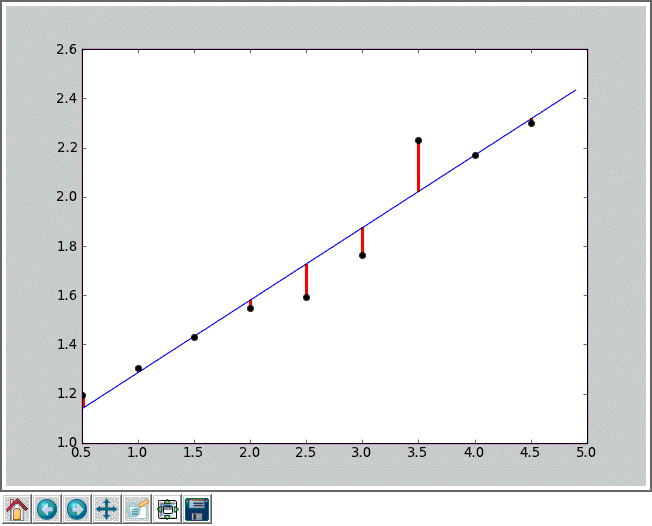
Wyobraźmy sobie, że nasze wyniki rzeczywiście są od siebie zależne liniowo i powinny układać się na wykresie na prostej. Ponieważ jednak są one obarczone błędami pomiarowymi, w rzeczywistości ich położenia są rozrzucone wokół położeń teoretycznych. Na rysunku widzimy punkty doświadczalne (czarne), teoretyczną prostą, na której ich oczekiwaliśmy (niebieska) i różnice w położeniu (czerwone).
Różnicę odległości i-tego punktu doświadczalnego (xi, yi) od punktu (xi, ỹi) leżącego na prostej y = A + B x możemy więc zapisać jako |yi − (A + B xi)| — to jest długość czerwonej kreski na wykresie. Jeżeli potraktujemy sumę tych różnic ei jako błąd doświadczalny e, możemy spróbować policzyć, dla jakich wartości parametrów prostej A i B błąd ten jest najmniejszy. Taką prostą będziemy traktować jako najlepiej opisującą nasze punkty doświadczalne.
Mamy więc błąd doświadczalny w postaci:
- [math]e=\sum_{i=1}^{n}e_i=\sum_{i=1}^{n}|y_i-\tilde{y}_i|=\sum_{i=1}^{n}|y_i-(A+Bx_i)|[/math]
Aby znaleźć minimum tej funkcji (od A i B) należy policzyć pochodne po obu parametrach i przyrównać je do zera. Ponieważ funkcja wartości bezwzględnej nie ma w zerze pochodnej, korzystamy z trochę innego podejścia, minimalizując nie wartość bezwzględną, ale kwadrat sumy błędów doświadczalnych:
- [math]e^2=\sum_{i=1}^{n}(e_i)^2=\sum_{i=1}^{n}(y_i-(A+Bx_i))^2[/math]
Jako, że będziemy szukać minimum sumy kwadratów błędów, metoda nazywa się metodą najmniejszych kwadratów. Zapiszmy jeszcze parametry prostej jako wektor [math]a=\left(\begin{matrix} A\\B \end{matrix} \right)[/math] oraz wprowadźmy jeszcze
- [math]X=\left(\begin{matrix} 1&x_1\\1&x_2\\\vdots&\vdots\\1&x_n\end{matrix} \right)[/math] , [math]e=\left(\begin{matrix} e_1\\e_2\\\vdots\\e_n\end{matrix} \right)[/math] oraz [math]Y=\left(\begin{matrix} y_1\\y_2\\\vdots\\y_n\end{matrix} \right)[/math].
Wtedy
- [math]e=y-Xa[/math]
i mamy (w zapisie wektorowym)
- [math]e^2=e^{\mathrm{T}}e=(y-Xa)^\mathrm{T}(y-Xa)=y^\mathrm{T}y-y^\mathrm{T}Xa-(Xa)^\mathrm{T}y+(Xa)^\mathrm{T}(Xa)[/math].
Ponieważ wynik (e2) jest skalarem, wszystkie elementy powyższej sumy też są skalarami i transpozycja nie zmieni ich wartości. Stosując wzór na transpozycję iloczynu [math](AB)^\mathrm{T}=B^\mathrm{T}A^\mathrm{T}[/math] oraz powyższą uwagę do [math]y^\mathrm{T}(Xa)=(y^\mathrm{T}(Xa))^\mathrm{T}=(Xa)^\mathrm{T}y[/math] dostajemy
- [math]e^2=y^\mathrm{T}y-2(Xa)^\mathrm{T}y+(Xa)^\mathrm{T}(Xa)=y^\mathrm{T}y+a^\mathrm{T}X^\mathrm{T}Xa-2a^\mathrm{T}X^\mathrm{T}y[/math].
Różniczkując to wyrażenie po [math]a[/math] i przyrównując do zera dostajemy warunek
- [math]2X^\mathrm{T}Xa-2X^\mathrm{T}y=0[/math].
Dostajemy więc ostatecznie równanie
- [math]X^\mathrm{T}Xa=X^\mathrm{T}y[/math],
które jest układem równań liniowych i umiemy je rozwiązać (na przykład metodami przedstawionymi w niniejszym rozdziale).
Uwaga: patrząc na to równanie można by powiedzieć, że możemy je sprowadzić do postaci [math]Xa=y[/math]. Taka postać, choć wydaje się prostsza, nie da się rozwiązać metodami przeznaczonymi dla układów równań liniowych, gdyż macierz [math]X[/math] nie jest w ogólności kwadratowa. Dopiero macierz [math]X^\mathrm{T}X[/math] jest kwadratowa, i, jeśli jej wyznacznik jest różny od zera, układ ma rozwiązanie.
Uwaga 2: w Matlabie jest do dyspozycji operator lewostronnego dzielenia macierzy, który można wykorzystać do rozwiązania układu [math]Xa=y[/math]. Jeśli skonstruujemy macierze [math]X[/math] i [math]y[/math], poleceniem a = X \ y otrzymujemy rozwiązanie.
Łatwo się przekonać, że ten sam formalizm możemy zastosować do dopasowania (ang. fit) wielomianów dowolnego stopnia. Całe zagadnienie będziemy rozwiązywać w analogiczny sposób, dostając na końcu do rozwiązania identyczne równanie na wektor parametrów — współczynników poszukiwanego wielomianu. Macierz [math]X[/math] nazywa się macierzą Vandermonda:
- [math]X=\left(\begin{matrix} 1&x_1&x_1^2&\dots&x_1^k\\ 1&x_2&x_2^2&\dots&x_2^k\\ \vdots&\vdots&\vdots&&\vdots\\ 1&x_n&x_n^2&\dots&x_n^k\end{matrix} \right)[/math] dla wielomianu [math]y=a_0+a_1x+a_2x^2+\dots+a_kx^k[/math].
Oczywiście możemy minimalizować sumę kwadratów błędów również dla innego typu (niż wielomian) zakładanej teoretycznie funkcji, ale wtedy e = (y − ỹ) ≠ (y − Xa) i różniczkowanie prowadzi do innych wzorów, za każdym razem trzeba je wyprowadzić osobno.
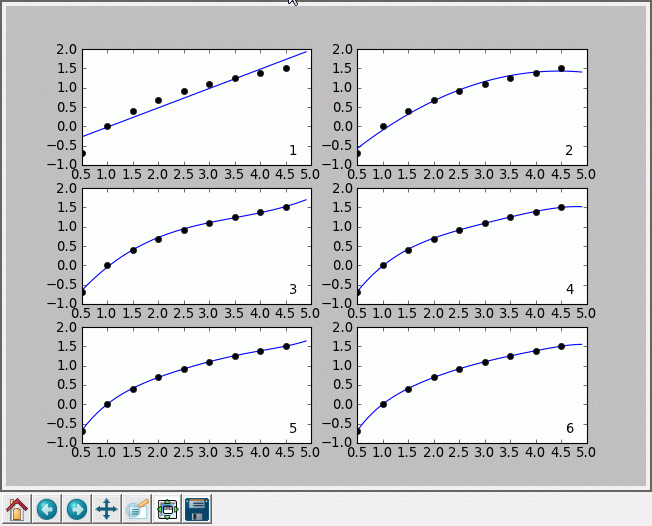
Rysunek poniżej przedstawia wynik dopasowania wielomianów stopni od 1 do 6 do fragmentu funkcji logarytmicznej (na odcinku 0,5-4,5).
Napisz program, który dla danego zestawu punktów na płaszczyźnie:
- skonstruuje macierz Vandermonda;
- rozwiąże odpowiedni układ równań i znajdzie współczynniki wielomianu interpolacyjnego;
- narysuje punkty i wielomian wynikowy.
Napisz program, który dla danego zestawu punktów na płaszczyźnie dopasuje i narysuje wielomian interpolacyjny korzystając z funkcji polyfit i polyval modułu numpy.
Efekt Rungego
Patrząc na przykład dopasowania wielomianów z poprzedniego rozdziału możemy odnieść wrażenie, że im wyższy stopień wielomianu użytego do dopasowania, tym dopasowanie stanie się lepsze (chyba, że dane oryginalnie były zależne liniowo lub wielomianem niższego rzędu). W naszym przykładzie z funkcją logarytmiczną tak rzeczywiście jest — wraz ze zwiększaniem stopnia wielomianu, dopasowanie poprawia się.
Może więc należy zawsze stosować wielomiany wysokiego rzędu? Pomijając fakt sensowności dopasowywania arbitralnie wybieranych funkcji do danych doświadczalnych, z czysto matematycznego punktu widzenia taka procedura również w którymś momencie przestaje dawać dobre wyniki.
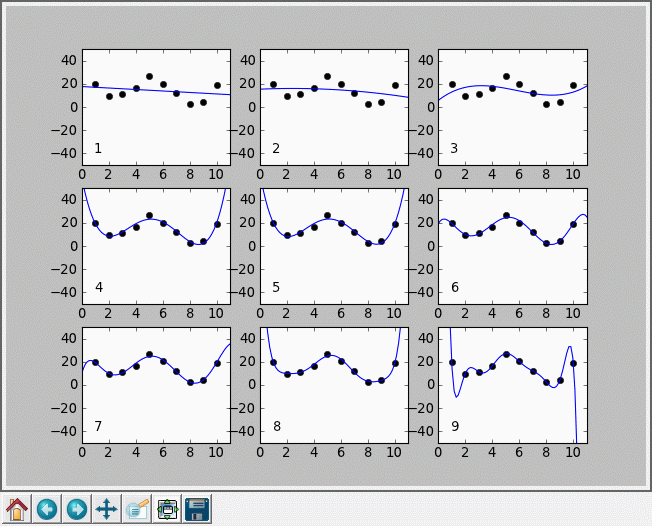
Poniżej narysowane są wielomiany stopnia 1-9 dopasowane do zestawu dziesięciu punktów.
Widzimy, że z początku jakość dopasowania wzrasta. Niestety, zwiększając dalej stopień wielomianu obserwujemy, że chociaż krzywa przechodzi coraz bliżej punktów, to jednocześnie oddala się coraz bardziej od nich w obszarze poza granicami obejmowanymi przez nasze dane. W granicznym przypadku wielomian 9 stopnia, posiadający 10 parametrów, dopasowaliśmy do 10 punktów, wykorzystując wszystkie stopnie swobody do zmiany wartości tych parametrów. Wielomian ten przechodzi dokładnie przez każdy z naszych punktów, ale pomiędzy nimi zdecydowanie nie zachowuje się jak oczekiwana funkcja interpolująca. Zjawisko to jest w szczególności widoczne tym bardziej im bliżej brzegów obszaru jesteśmy. Nazywamy je efektem Rungego (Carl Runge — matematyk niemiecki).
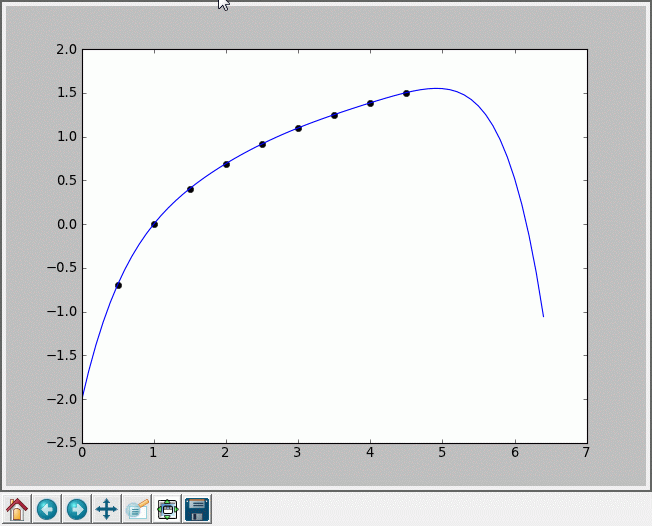
Rysunek poniżej przedstawia wielomian stopnia 6 dopasowany do funkcji logarytmicznej. Ponieważ zakres osi x został rozszerzony w stosunku do obrazka z poprzedniego rozdziału, tutaj też widzimy, że poza obszarem dopasowywanych punktów funkcja nie spełnia naszych oczekiwań.
Napisz program rysujący wykres wielomianu stopnia n−1 dopasowanego do funkcji
- [math]y=\frac{1}{1+x^2}[/math]
obliczonej w n równo oddalonych punktach z przedziału [−5, 5]. Prześledź zachowanie się takich wielomianów dla różnych wartości n.
Funkcje sklejane
Jak widzieliśmy, stosowanie wielomianów do przybliżania różnych skomplikowanych funkcji ma swoje ograniczenia. Możliwe jest jednak inne podejście: rozpatrzmy dwa sąsiadujące punkty danych. Przez każde dwa punkty możemy przeprowadzić prostą otrzymując linię łamaną przechodzącą przez wszystkie nasze punkty. Taka łamana linia jest często stosowanym zgrubnym przybliżeniem złożonych krzywych. Krok dalej stanowi dopasowanie wielomianów wyższego stopnia do kolejnych sąsiednich punktów w taki sposób, aby wypadkowa funkcja przechodziła przez wszystkie punkty, była ciągła oraz miała ciągłą pochodną (lub też ciągłe pochodne do stopnia n−1 w przypadku użycia wielomianu stopnia n) w miejscach styku. W ogólności krzywą taką, powstałą z odcinków wielomianów, nazywamy funkcją sklejaną (ang. spline).
Najbardziej popularne są funkcje sklejane stopnia 3 (ang. cubic splines). W tym przypadku do każdej pary sąsiednich punktów danych dopasowujemy funkcję postaci ax3+bx2+cx+d. Dla wszystkich dopasowywanych funkcji musimy spełnić warunek ciągłości samej funkcji, jej pierwszej i drugiej (n=3, n−1=2) pochodnej. Przy n+1 punktach danych wyznaczamy n różnych funkcji (n przedziałów) czyli 4n współczynników. Ze wszystkich warunków ciągłości na styku przedziałów dostaniemy 3(n−1) równań. Ponieważ mamy też wartości samej funkcji w n+1 punktach (zwanych węzłami, ang. knots), w sumie mamy 4n−2 równań na 4n niewiadomych.
Pozostałe dwa równania musimy określić wybierając warunki brzegowe. Mamy tu kilka typowych możliwości:
- Możemy przyjąć, że druga pochodna naszej funkcji w punktach brzegowych jest równa zero (dwa równania). Otrzymujemy w ten sposób tzw. naturalne funkcje sklejane (ang. natural spline). Czasem nazywa się taki wybór dopasowaniem z końcami swobodnymi.
- Możemy założyć, że funkcja jest okresowa, a nasz zestaw węzłów obejmuje jeden okres. Wtedy zakładamy, że pierwsza i druga pochodna (dwa równania) są sobie równe na obu końcach przedziału (czyli dla x1 i xn+1).
- Możemy wybrać sobie wartości pierwszej pochodnej na obu końcach przedziału (dwa równania). Wybór taki nazywa się dopasowaniem z końcami usztywnionymi. Funkcja poza zakresem dopasowania ma postać linii prostych o zadanych nachyleniach.
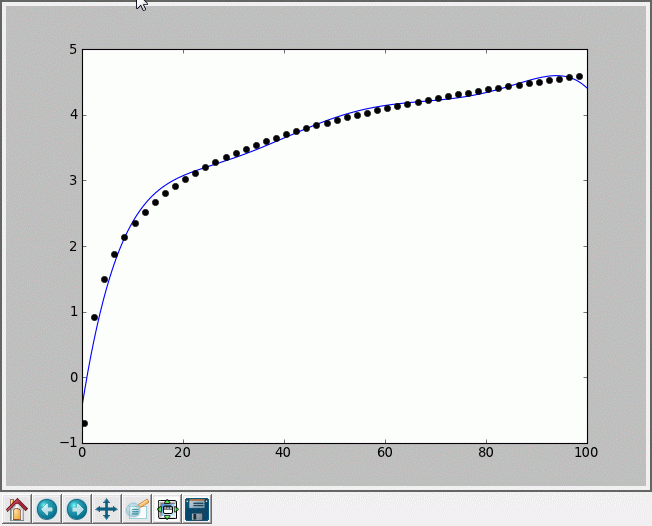
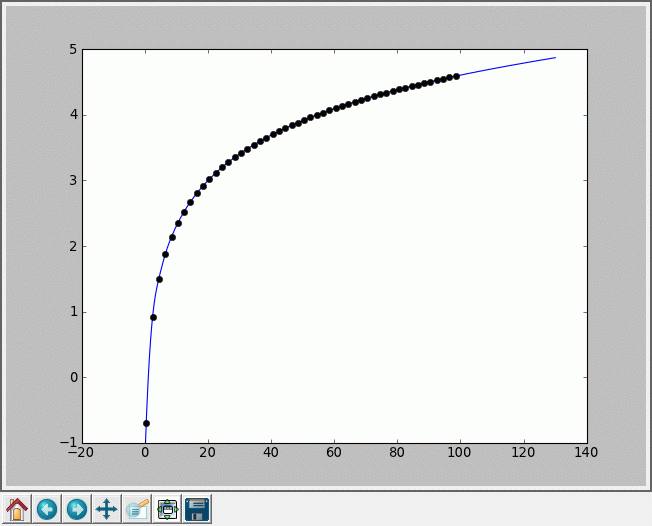
Rysunki poniżej przedstawiają dopasowanie wielomianu stopnia 6 oraz funkcji sklejanej stopnia 3 do funkcji logarytmicznej w zakresie 0,5-100 w kilkudziesięciu punktach. Funkcja sklejana „optycznie” znacznie lepiej dopasowuje badaną krzywą, nawet w części ekstrapolacyjnej, poza zakresem posiadanych punktów.
Napisz program dopasowujący i rysujący funkcję sklejaną stopnia 3 do danego zestawu punktów stosując procedury splrep i splev z modułu scipy.interpolate.
Napisz program dopasowujący funkcję sklejaną stopnia 3 do zbioru punktów pomiarowych opisujących położenie wahadła tłumionego w czasie, zmierzone z błędem (stosując procedury splrep i splev z modułu scipy.interpolate).
Uwaga: czy funkcja sklejana przechodząca przez wszystkie punkty ze zbioru będzie dobrym wyborem?
Czy możemy powiedzieć coś o parametrach tego wahadła na podstawie dopasowanej funkcji sklejanej?
Równania różniczkowe i całkowanie
Równania ruchu
Na zajęciach z „Technologii informacyjnej” zetknęliśmy się już przez chwilę z zagadnieniem rozwiązywania równania różniczkowego na przykładzie równań ruchu. W tym rozdziale powtórzymy podobny przykład, który, mamy nadzieję, pomoże w zrozumieniu tego zagadnienia.
Gdy rozwiązujemy zwykłe równanie z niewiadomą wielkością, jako rozwiązanie otrzymujemy poszukiwaną liczbę. Gdy rozwiązujemy równanie różniczkowe rozwiązaniem jest nie liczba ale funkcja. Na przykład równanie y′ = x ma rozwiązanie w postaci funkcji y = x2/2. Taki zwięzły wynik otrzymujemy, gdy umiemy rozwiązać nasze równanie w sposób analityczny, czyli gdy znamy konkretną postać funkcji będącej rozwiązaniem. My jednak będziemy rozwiązywać równania różniczkowe w sposób numeryczny nawet, gdy nie tylko nie znamy postaci funkcji-rozwiązania, ale nawet nie musimy znać wzoru funkcji występującej w równaniu. To co właściwie wiemy o tych funkcjach? Znamy ich wartości dla pewnego zakresu ich argumentów. Wynikiem też będzie zestaw wartości funkcji-rozwiązania dla pewnego zakresu jej argumentów. Nie będziemy znać wzoru opisującego rozwiązanie, ale będziemy mogli narysować jego wykres.
Poprzednio rozwiązywaliśmy równanie ruchu masy zawieszonej na sprężynie. Teraz rozwiążemy równanie ruchu wahadła matematycznego, bez stosowania przybliżenia małych drgań. Wychodząc z drugiej zasady dynamiki, po przekształceniach pozostaje nam do rozwiązania równanie na kąt α (odchylenia wahadła od pionu):
- [math] \frac{d^2\alpha}{dt^2} = - \omega ^2 \sin\alpha [/math]
Funkcje całkujące równania różniczkowe w SciPy radzą sobie tylko z równaniami i układami równań pierwszego rzędu. Musimy zatem przepisać nasze równanie na układ równań pierwszego rzędu. Można to zrobić wprowadzając dodatkową zmienną. Tą zmienną jest v = dα/dt (prędkość kątowa wahadła). Teraz nasz układ wygląda tak:
- [math] \left\{ \begin{array}{l} \frac{d\alpha}{dt} = v \\ \frac{dv}{dt} = - \omega^2 \sin \alpha \end{array} \right. [/math]
Wprowadzając wektor zmiennych
- [math]\vec{x} = \left( \begin{matrix} \alpha\\ v \end{matrix}\right) [/math]
dostajemy równanie postaci
- [math]\frac{d\vec{x}}{dt} = f(\vec{x}) = f(\alpha,v)[/math]
czyli
- [math]\frac{d}{dt}\vec{x} =\left( \begin{matrix} v\\ -\omega^2 \sin\alpha \end{matrix} \right)[/math]
# -*- coding: utf-8 -*-
from scipy.integrate import odeint
import numpy as np
import pylab as p
def prawa_strona_rownania(w, t, params):
''' Argumenty:
w: wektor stanu - u nas krotka (alfa, v)
t: czas
params: wektor parametrów - u nas krotka (omega_kwadrat,)
W wektorze f funkcja zwraca
obliczone dla danego wektora stanu
wartości prawej strony równania
'''
(alfa,v) = w # dla czytelności równania wypakowuję zmienne z wektora "w"
(omega_kwadrat,) = params # i podobnie z parametrami "params"
# poniżej do tablicy f w kolejnych wierszach wpisuję
# kolejne prawe strony równań stanowiących układ
f = [v, # wartość pochodnej d(alfa)/dt
-omega_kwadrat*np.sin(alfa)] # wartość pochodnej dv/dt
return f
if __name__ == '__main__':
t = np.linspace(0, 10, 101) # punkty czasu, w których obserwujemy wahadło
params = [2] # wartość omega**2 (u nas wynosi 2)
w = [0, 2.82] # warunek początkowy (t=0) dla alfa i v
print "Wektor stanu w chwili początkowej: ",
print prawa_strona_rownania(w, t[0], params)
wynik = odeint(prawa_strona_rownania, w, t, args=(params,) )
# argumentami odeint są:
# - nazwa funkcji,
# - wektor stanu początkowego,
# - wektor zawierający chwile czasu, dla których ma być zwrócony stan układu
# - krotka zawierająca dodatkowe parametry, które mają być przekazane do funkcji
# opisującej prawe strony równań
alfa = wynik[:, 0] # wszystkie wiersze kolumny 0 - położenia
v = wynik[:, 1] # wszystkie wiersze kolumny 1 - prędkości
p.plot(t,alfa, t,v)
p.legend(('$\\alpha$', 'v'))
p.grid(True)
p.show()
Funkcja odeint oczekuje przynajmniej trzech parametrów: funkcji obliczającej pochodną poszukiwanej funkcji (albo pochodne poszukiwanych funkcji w przypadku układu równań), warunku początkowego dla szukanych funkcji oraz sekwencji punktów czasu, w których będzie obliczone rozwiązanie. W naszym przypadku będą to:
- nazwa funkcji obliczającej pochodne — prawa_strona_rownania, zwraca wektor [math][\dot{x},\ \dot{v}][/math], czyli [math][v,\ -\omega ^2 \sin \alpha][/math];
- warunek początkowy — lista w = [0, 2.82], czyli [α(0), v(0)];
- sekwencja punktów czasu — wektor t = np.linspace(0,10,101), czyli [0, 0,1, 0,2,... 9,9, 10].
U nas jest jeszcze czwarty parametr (nazwany, o nazwie args). Powinna być to krotka zawierająca dodatkowe parametry, jakich może potrzebować funkcja obliczająca wartości pochodnych. My mamy jeden taki dodatkowy parametr: ω2, która w naszym programie jest przechowywana w zmiennej params. Tworzymy więc z niej krotkę jednoelementową i przekazujemy ją funkcji odeint jako czwarty parametr. Zostanie ona użyta podczas liczenia prawej strony równań rozwiązywanego układu, czyli w funkcji prawa_strona_rownania.
Uwaga: numeryczne rozwiązywanie równań różniczkowych jest szeroką dziedziną metod obliczeniowych, obejmującą wiele szczegółowych zagadnień dotyczących warunków stosowalności wybranych rozwiązań, uzyskiwanej dokładności czy szybkości algorytmu. O istotności wyboru kroku czasowego na dokładność wyniku mówiliśmy już w kusie „Technologii informacyjnej” (rozdział „Matplotlib”, przykład o ruchu jednostajnie przyspieszonym). W niniejszym rozdziale zdajemy się całkowicie na obliczeniową procedurę biblioteczną, skupiając się na praktycznym jej zastosowaniu.
Jaką różnicę obserwujemy w stosunku do rozwiązania w przybliżeniu małych drgań?
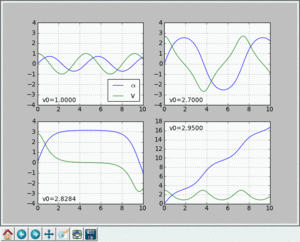
Dodaj do ruchu wahadła tłumienie w postaci siły oporu zależnej od prędkości ze współczynnikiem β = 0,3. Rozwiąż równanie ruchu i zaobserwuj zachowanie się wahadła dla różnych wartości prędkości początkowej.
Zauważ, że dla większych prędkości początkowych po pewnym czasie kąt ustala się na wielokrotności 2π. Co to oznacza?
Zmień wartość tłumienia i zaobserwuj zmiany w zachowaniu wahadła.
Bazując na powyższym przykładzie znajdź zależność od czasu położenia i prędkości piłki o masie m = 300 g spadającej swobodnie w ziemskim polu grawitacyjnym (g = 9,81 m/s2).
Porównaj swoje rozwiązanie z rozwiązaniem analitycznym tego problemu.
Dodaj siłę oporu zależną od prędkości i zaobserwuj zmiany w rozwiązaniu.
Dwie małe jednakowe kulki o masach m = 900 g, naładowane jednakowymi ładunkami elektrycznymi Q = 10−13 C, znajdują się w odległości d = 1 cm od siebie. W chwili początkowej kulki spoczywają. Znajdź zależność od czasu położenia i prędkości jednej z kulek dla t ∈ [0, 1] s.
- Przyjmij [math]k=\frac{1}{4\pi\varepsilon_0}=9\cdot 10^9\ \frac{\mathrm{Nm^2}}{\mathrm{C^2}}[/math].
Całkowanie funkcji metodą trapezów
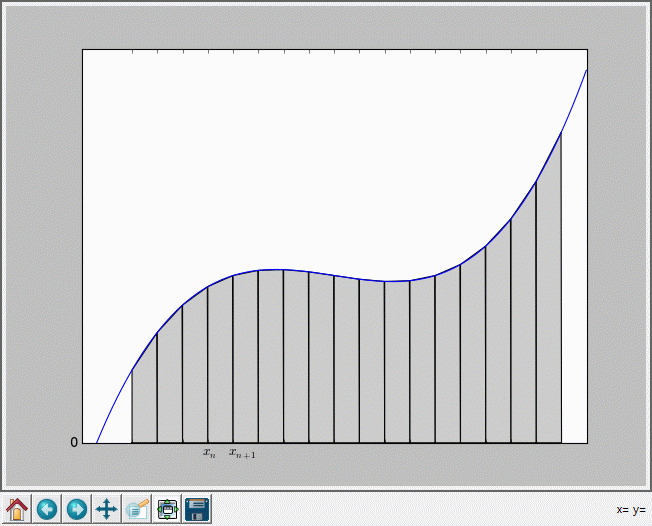
Metoda trapezów jest prostą techniką liczenia całek oznaczonych funkcji o znanej postaci analitycznej lub numerycznej. Ponieważ wartość całki oznaczonej odpowiada polu figury zawartej między osią OX a wykresem funkcji, spróbujmy to pole w przybliżeniu policzyć. Przybliżenie polegać będzie na zastąpieniu oryginalnej funkcji funkcją sklejaną pierwszego stopnia.
Wybieramy więc zestaw n+1 punktów i liczymy dla nich wartości funkcji. W przypadku funkcji zadanej numerycznie, użyjemy po prostu posiadanych wartości. Łączymy sąsiednie wartości funkcji prostymi. Pole pod taką funkcją jest sumą pól w każdym przedziale między kolejnymi parami punktów, zaś pole w każdym z przedziałów to pole odpowiedniego trapezu. Można pokazać, że gdy odległości między punktami zbiegają do zera, pole „całki trapezowej” zbiega do prawdziwej wartości całki oznaczonej danej funkcji ciągłej.
W przypadku funkcji zadanej numerycznie nie możemy po prostu zagęścić siatki punktów, aby polepszyć oszacowanie całki, gdyż nie znamy wartości funkcji pomiędzy posiadanymi punktami. Możemy wtedy interpolować funkcję w obszarze pomiędzy posiadanymi wartościami stosując np. interpolację wielomianową lub funkcjami sklejanymi. Taką sztucznie „zagęszczoną” siatkę punktów wykorzystujemy do polepszenia oszacowania wartości naszej całki.
Napisz program obliczający całkę oznaczoną metodą trapezów dla danego zestawu punktów doświadczalnych.
Napisz program obliczający pole pod zadaną funkcją metodą trapezów. Policz całkę dla wybranej funkcji analitycznej i porównaj wynik z wynikiem otrzymanym za pomocą własnego programu.
Napisz program obliczający całkę oznaczoną metodą trapezów dla danego zestawu punktów doświadczalnych, do których dopasowano
- wielomian;
- funkcję sklejaną.
Policz całkę dla wybranej funkcji analitycznej i porównaj wynik z wynikiem otrzymanym za pomocą własnego programu.