TI/Zadanie zaliczeniowe

Wstęp

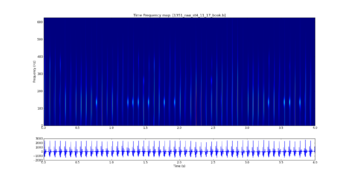
Projekt będzie polegać na napisaniu programu, który wczyta pliki generowane przez dekompozycję Matching Pursuit i następnie narysuje mapę czas-częstość danego sygnału oraz sam sygnał. Efekt powinien wyglądać mniej-więcej jak na rysunku %i 1. Przykładowe pliki po dekompozycji są zalinkowane na końcu.

Pytania proszę kierować na adres Piotra Milanowskiego lub z zapytaniem przyjść na zajęcia/konsultacje.

• UWAGA!!!! Poniżej przedstawione są poprawki do projektu:
  • W sekcji nagłówka: po identyfikatorze nagłówka i rozmiarze nagłówka, jest odpowiedni identyfikator pola nagłówka (adres, data, informacja o sygnale i dekompozycji) a następnie rozmiar pola W FORMACIE uchar (1 bajt) (a nie jak w zadaniu projektu uint32). Rozmiar ten dotyczy tylko pól adres i data; pola informacja o sygnale i dekompozycji zajmują odpowiednio 10 i 13 bajtów (float32, float32, uint16 = 4+4+2 bajty i float32, float32, float32, char = 4+4+4+1 bajty)

(Błąd dostrzeżony przez Wojciecha Raszkę)

• • Nie wszystkie parametry atomów są przedstawione w jednostkach SI:
    • pozycja w czasie i skala są zapisane w punktach (do sekund konwertujemy dzieląc przez częstość próbkowania)
    • częstotliwość zapisana w formie znormalizowanej (do hertzów konwertujemy mnożąc przez częstość próbkowania i dzieląc przez 2π)
    • amplituda zapisana jest w punktach (konwersja do mikrowoltów polega na podzieleniu przez liczbę punktów na mikrowolt)
    • modulus i faza nie wymagają konwersji
  • Plik 1351_raw_st4_106_5_book.b zawiera błędny nagłówek. Proszę testować na pliku 1351_raw_st4_11_17_book.b.
  • Dane są zapisane w formacie BIG ENDIAN. Oznacza to, że korzystając z funkcji struct.unpack trzeba do napisu oznaczającego format danych dodać na początku symbol '>'. Na przykład chcąc przeformatować napis na floaty: struct.unpack(">f", napis)
  • Implementacja delty diracka na mapie M(t,f) czas częstość to: [math]M(t0, f) = (a_iK_i)^2[/math]np.ones(#rozdzielczosć w częstotliwości), gdzie [math]a_i, K_i, t0[/math] to dane odczytane z pliku (modulus, amplituda, pozycja w czasie)
  • Implementacja delty diracka na mapie M(t,f) czas częstość to: [math]M(t, f0) = (a_iK_i)^2[/math]np.ones(#rozdzielczosć w czasie), gdzie [math]a_i, K_i, f0[/math] to dane odczytane z pliku (modulus, amplituda, pozycja w częstości)
  • Do narysowania atomu typu delta Diracka należy wszystkie odczytane parametry atomu wstawić do wzoru Gabora%i 1. Kilka z nich będzie 0, ale proszę się tym nie przejmować.
  • Rozmiar atomu jest podany w formacie uchar

Przykład działania programu. Górny rysunek to mapa czas-częstość sygnału widocznego na dolnym rysunku.

Opis plików dekompozycji

Matching Pursuit

Sama metoda dekompozycji Matching Pursuit powinna być dobrze znana po zajęciach z Analizy Sygnałów; nie będzie więc tutaj omawiana w szczegółach. Wystarczające będzie przypomnienie, że sygnał dekomponowany jest na sumę funkcji Gabora, tj. na funkcje o wzorze:

[math]g_\gamma \left(t\right) = K\left(\gamma \right)\exp \left(-{\pi }\frac{\left(t-u\right)^2}{\sigma ^2}\right) \cos \left(2{\pi }f_0\left(t-u\right)+\phi \right)[/math]

gdzie [math]\gamma =\left\lbrace u,f_0,\sigma ,\phi \right\rbrace [/math] oznacza zbiór parametrów funkcji, odpowiednio: przesunięcia w czasie ([math]u[/math]), częstotliwości ([math]f_0[/math]), pewnej miary szerokości w czasie ([math]\sigma [/math]) i fazy ([math]\phi [/math]). Parametr [math]K(\gamma )[/math] normalizuje funkcję.

Mapy czas–częstość

Mając sygnał w postaci sumy [math]M[/math] funkcji gabora, można przedstawić gestość jego energii w przestrzeni czas-częstość. Jeśli mamy sygnał w postaci:

[math]s\left(t\right) = \sum ^M_{i=1}a_ig_{\gamma _i}\left(t\right)[/math]

to gęstość energii wynosi:

[math]\begin{matrix} E_s\left(t,f\right) &=& \sum ^M_{i=1}a_i^2W_{\gamma _i}\left(t,f\right) \end{matrix}[/math]

gdzie [math]W_{\gamma _i}(t,f)[/math] to transformata Wigner-Villa:

[math]W_s\left(t,f\right) = \int _{\mathbb {R}}s\left(t+\frac{\tau }{2}\right)s\left(t-\frac{\tau }{2}\right)e^{-2{\pi }i{f}\tau }d\tau [/math]

a [math]a_i[/math] to pewien współczynnik i-tej funkcji gabora wyznaczony przy dekompozycji.

Transformata Wigner-Villa funkcji Gabora wnosi:

[math]\begin{matrix} W_{\gamma }\left(t,f\right) &=& K\left(\gamma \right)^2\sqrt{2{\pi }}\sigma e^{-2\sigma ^{-2}(t-u)^2}e^{-2{\pi }^2\sigma ^2(f_0 - f)^2} \end{matrix}[/math]

Opis pliku .b

Wynik działania algorytmu MP zapisywany jest do plików z rozszerzeniem .b. Są to pliki binarne; każdy można podizelić na 3 części opisane poniżej.

Początek

Pierwsze 6 bajtów pliku to litery (w ASCII) oznaczające wersję programu dekomponującego. Następnie może być komentarz: kolejny bajt pliku to idetyfikator (uchar); jeśli wartość tego bajtu to 1, następne 4 bajty (uint32) to długość komentarza. Potem jest komentarz o zadanej długości.

Nagłówek

Następny bajt to kolejny identyfikator. Jeśli jego wartość wynosi 2, mamy do czynienia z nagłówkiem. Następne 4 bajty (uint32) określają rozmiar nagłówka (w bajtach).

W sekcji nagłówka mogą być następujące pola, każde poprzedzone odpowiednim identyfikatorem (uchar) i rozmiarem pola (uint32):

• identyfikator 3: adres www - napis o zadanym rozmiarze
• identyfikator 4: data - napis o zadanym rozmiarze
• identyfikator 5: informacja o sygnale - kolejno częstość próbkowania (4 bajty - float32), liczba punktów na mikrowolt (4 bajty - float32), liczba kanałów (2 bajty - uint16)
• identyfikator 6: informacja o dekompozycji - kolejno wyjaśniony procent energii (4 bajty - float32), maksymalna liczba iteracji (4 bajty - uint32), rozmiar słownika (4 bajty - uint32), typ słownika (1 bajt - char)

Dane

Identyfikator danych to 7. Następnie jest długość tego segmentu danych (uint32). Potem liczba określająca numer epoki i rozmiar epoki (odpowiednio uint16 i uint32).

Teraz może być albo sygnał przed dekompozycją (identyfikator 8) albo atomy (identyfikator 9).

• W przypadku sygnału, po identyfikatorze jest rozmiar pola, a następnie numer kanału (uint16). Następnie jest sygnał zapisany w formacie float32 i ma rozmiar określony przez rozmiar epoki.
• W przypadku atomów, kolejnym bajtem po identyfikatorze i rozmiarze jest numer kanału (uint16) Następnie po kolei są atomy. Każdy zaczyna się od identyfikatora określającego typ atomu (dirac: 10, gauss: 11, sinus: 12, gabor: 13). Potem jest liczba (uchar) określająca rozmiar atomu. Następnie są parametry atomu, każdy w formacie float32: modulus (współczynnik [math]a_i[/math] przy dekompozycji %i 2), amplituda (współczynnik normujący [math]K(\gamma )[/math] w %i 3), pozycja w czasie, skala, pozycja w częstości i faza. Należy zauważyć, że w zależności od typu atomu, nie wszystkie parametry będą zapisane. Dla delty Diraca są tylko pierwsze trzy (modulus, amplituda, pozycja w czasie); dla funkcji Gaussa pierwsze cztery (modulus, amplituda, pozycja w czasie i skala); dla funcji sinus modulus, amplituda, pozycja w częstości i faza. Tylko dla funkcji Gabora zapisane są wszystkie parametry.

Podsumowanie

Podsumowując każdy segment informacji zaczyna się od identyfikatora i długości danego segmentu. Identyfikatory to:

1. Komentarz
2. Nagłówek
3. Adres www
4. Data
5. Informacje o sygnale
6. Informacje o dekompozycji
7. Dane
8. Początkowy sygnał
9. Atomy
10. Delta Diraca
11. Funkcja Gaussa
12. Sinus
13. Funkcja Gabora

Wskazówki

Rysowanie atomów

Na mapie czas-częstość funkcja delta Diraca to pionowa linia o stałym czasie i przebiegająca wszystkie częstości. Jej wartość to odczytana z pliku wartość modulus podniesiona do kwadratu razy amplituda podniesiona do kwadratu.

Podobnie sinus: na mapie czas-częstość to pozioma linia o stałej częstotliwości i przebiegająca wszystkie czasy.

Gausa można narysować korzystając z równania %i 3 przyjmując jako częstotliwość i fazę 0.

Wyliczanie mapy czas-częstość

Za pomocą równań %i 2 i %i 3 można wyznaczyć gęstość energii sygnału. Do wyznaczenia mapy pojedynczego atomu (korzystając z %i 3) można wykorzystać fakt, że mnoży się tu funkcję zależną tylko od czasu (nazwijmy ją [math]f(t)[/math]) przez funkcję zależną tylko od częstotliwości ([math]g(\omega )[/math]). Można więc najpierw policzyć wartości funkcji [math]f(t)[/math] dla zadanych chwil czasowych, następnie wartości funkcji [math]g(\omega )[/math] dla zadanych częstotliwości i przemnożyć te dwa wektory albo korzystając z funkcji liczącej iloczyn zewnętrzny, albo korzystając z reguł broadcastingu numpy.