Uczenie maszynowe i sztuczne sieci neuronowe/Wykład Ocena jakości klasyfikacji

powrót

Ocena klasyfikatorów binarnych

Klasyfikatory binarne to te, których zadaniem jest przypisanie danemu przykładowi jednej z dwóch możliwych klas. Przykładem takiego klasyfikatora jest znana już nam regresja logistyczna.

Jako przykład roboczy rozważmy problem klasyfikowania osób na zdrowe i chore na podstawie objawów. Klasyfikator jako cechy przyjmuje na wejściu objawy (przedstawione w postaci numerycznej) i zwraca wynik klasyfikacji (testu). Zakładamy, że mamy dane zawierające zarówno objawy O jak i faktyczny stan osoby W dla pewnej grupy osób (W może mieć dwie wartości: zdrowy, chory). Mamy też pewien klasyfikator, który realizuje odwzorowanie: [math] H(O) \rightarrow K [/math] I tu podobnie, wynik klasyfikatora K może przyjąć jedną z dwóch wartości: zdrowy lub chory. W praktyce medycznej najczęściej mówimy, że pozytywny wynik testu wskazuje na chorobę.

Typy błędów

Porównując wyniki W i K możemy mieś cztery sytuacje, :

		Stan faktyczny		Razem
		chory	zdrowy
wynik klasyfikacji	chory (wynik testu pozytywny)	TP: prawidłowa decyzja pozytywna	FP (błąd I typu: wynik fałszywie pozytywny)	P'
	zdrowy (wynik testu negatywny)	FN (błąd II typu: wynik fałszywie negatywny)	TN: prawidłowa decyzja negatywna	N'
Razem		P	N

Anglojęzyczna nomenklatura często stosowana do opisu tych możliwości to:

• TP: true positive, hit
• TN: true negative, correct rejection
• FP: false positive, false alarm, Type I error
• FN: false negative, with miss, Type II error

Miary

Jeśli mamy zbiór uczący o pewnej liczebności to dla każdego z elementów zbioru uczącego zachodzi jedna z powyżej opisanych możliwości. Dla całego zbioru uczącego mamy konkretne ilości przypadków każdego typu. Zliczenia tych przypadków są podstawą do stworzenia pewnych miar pozwalających na ocenę klasyfikatora. Miary oparte na tych definicjach to:

Czułość i specyficzność

• czułość: (inne spotykane nazwy: sensitivity, true positive rate TPR, hit rate, recall). Można ją interpretować jako prawdopodobieństwo, że klasyfikacja będzie poprawna pod warunkiem, że przypadek jest pozytywny. Prawdopodobieństwo, że test wykonany dla osoby chorej wykaże, że jest ona chora.

[math]TPR = \frac{TP}{ P} = \frac{TP} { TP+FN}[/math]

• specyficzność: (specificity (SPC), True Negative Rate). Prawdopodobieństwo, że klasyfikacja będzie poprawna, pod warunkiem, że przypadek jest negatywny. Prawdopodobieństwo, że dla osoby zdrowej test nie wykryje choroby.

[math]SPC = \frac{TN}{ N} = \frac{TN} { FP + TN} = 1 - FPR [/math]

Fałszywe alarmy

• częstość fałszywych alarmów ( false positive rate (FPR), fall-out): Jak dużej frakcji osób zdrowych test wyjdzie pozytywnie?

[math]FPR = \frac{FP}{ N} = \frac{FP}{ FP + TN} = 1-SPC[/math]

• częstość fałszywych odkryć: (false discovery rate (FDR)): Jak duża frakcja spośród pozytywnych wyników testu jest fałszywa?

[math]FDR = \frac{FP}{ FP + TP}[/math]

Własności predykcyjne: Precyzja

• precyzja pozytywna: (positive predictive value (PPV), precision). Odpowiada on na pytanie: Jeśli wynik testu jest pozytywny, jakie jest prawdopodobieństwo, że osoba badana jest chora?

[math]PPV = \frac{TP}{ TP + FP}[/math]

• precyzja negatywna: (negative predictive value (NPV).) Odpowiada on na pytanie: Jeśli wynik testu jest negatywny, jakie jest prawdopodobieństwo, że osoba badana jest zdrowa?

[math]NPV = \frac{TN }{ TN + FN}[/math]

Efekt częstości występowania

Częstość występowania ma znaczący wpływ na opisane powyżej wartości predykcyjne. Jako przykład przypuśćmy, że mamy test na pewną chorobę i charakteryzuje się on 99% czułością i 99% specyficznością. Załóżmy, że testowanych jest 2000 osób i częstość występowania choroby (w próbie) wynosi 50%, to znaczy 1.000 z nich są chore a 1000 z nich są zdrowe. W takiej sytuacji spodziewamy się około 990 wyników TP i 990 TN oraz około 10 wyników FP i 10 FN. Dodatnie i ujemne wartości predykcyjne będą 99%, tak więc możemy mieć wysokie zaufanie do wyniku.

Jednakże, w przypadku gdy częstość występowania choroby będzie wynosiła tylko 5%, czyli z 2000 osób tylko 100 jest chorych, wartości predykcji znacznie się zmienią. Prawdopodobnym rezultatem jest 99 TP, 1 FN, 1881 TN i 19 FP. Spośród 19 + 99 osób pozytywnych, tylko 99 naprawdę są chorzy - to znaczy, intuicyjnie, że biorąc pod uwagę, że wynik badania pacjenta jest dodatni, jest tylko PPV =0.84 szans, że jest on naprawdę chory. Z drugiej strony biorąc pod uwagę ujemny wynik testu pacjenta, jest tylko 1 szansa na 1882 (NPV= 0,0005 ), że ​​pacjent cierpi na chorobę, mimo ujemnego wynik testu.

Miary zbalansowane

Powyżej rozważane miary były sparowane, tzn. trzeba obie jednocześnie brać pod uwagę przy ocenie testu/klasyfikatora. Poniżej są definicje popularnych miar sprowadzonych do jednej liczby, która w pewnym stopniu opisuje całościowo wyniki.

• dokładność ( accuracy (ACC)): Prawdopodobieństwo prawidłowej klasyfikacji.

[math]ACC = \frac{TP + TN}{P + N}[/math]

• F1-score: średnia harminiczna z precyzji i czułości:

[math]F_1= 2 \frac{PPV \cdot TPR}{PPV+TPR}= \frac{2TP}{ 2TP+FP+FN}[/math]

Miara ta daje ocenę balansu między czułością a precyzją. Miara ta nie uwzględnia wyników prawdziwie negatywnych.

• [math]F_\beta[/math] jest uogólnieniem powyższej miary, które pozwala regulować za pomocą parametru [math]\beta[/math] wagę jaką przykładamy do PPV:

[math]F_\beta = (1+ \beta^2) \frac{PPV \cdot TPR}{PPV \beta^2 +TPR} [/math]

• współczynnik korelacji Matthews ( Matthews correlation coefficien)t:

[math] \text{MCC} = \frac{ TP \times TN - FP \times FN } {\sqrt{ (TP + FP) ( TP + FN ) ( TN + FP ) ( TN + FN ) } } [/math]

Ten współczynnik uwzględnia wyniki zarówno prawdziwie jaki i fałszywie pozytywne i negatywne i jest na ogół uważany jako zrównoważona miara, która może być stosowana nawet wtedy, gdy klasy są bardzo różnej liczebności. MCC jest w istocie współczynnikiem korelacji pomiędzy obserwowanymi i przewidywanymi klasyfikacjami binarnymi; zwraca wartość od -1 do +1. Współczynnik +1 odpowiada idealnej klasyfikacji, 0 nie lepiej niż losowe przypisanie wyniku i -1 oznacza całkowitą niezgodę między klasyfikacją i stanem faktycznym.

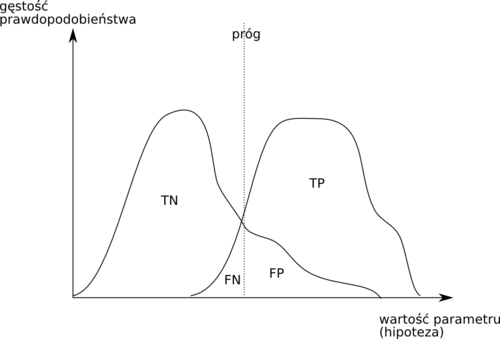
Klasyfikator z progiem

Powyżej rozważaliśmy test/klasyfikator dający wynik binarny. Łatwo jest sobie wyobrazić, że klasyfikator ma ciągłe wyjście, które po porównaniu z pewną wartością progową daje dopiero ostateczny wynik. W takiej sytuacji warto mieć metodę pozwalającą na świadomy wybór optymalnego progu i na ocenę klasyfikatora, abstrahując od konkretnej wartości progu. Takich możliwości dostarcza analiza ROC.

Prawdopodobieństwa podejmowania każdego rodzaju decyzji będą się zmieniały wraz z przesuwaniem progu podejmowania decyzji, czyli wartości hipotezy przy której zaliczamy przypadek do klasy 1.

Krzywe charakterystyki roboczej odbiorcy (ROC)

Krzywa ROC

każdy punkt na tej krzywej otrzymywany jest dla ustalonej wartości progu i ma współrzędne (1−specyficzność, czułość).

Demo ilustrujące powstawanie krzywej ROC: [1]

Krzywa ROC przydaje się do porównywania różnych klasyfikatorów oraz do wyboru punktu pracy (progu)

AUC: Pole powierzchni pod krzywą ROC ma interpretację probabilistyczną: jest to prawdopodobieństwo tego, że klasyfikator przydzieli wyższą rangę dla losowo wybranego przypadku pozytywnego niż negatywnego (zakładając, że wynik pozytywny ma wyższą rangę niż negatywny), w tym sensie jest ono blisko związane ze statystyką Wilcoxona [2]

Literatura

1. Fawcett, Tom (2006). "An Introduction to ROC Analysis". Pattern Recognition Letters 27 (8): 861–874. doi:10.1016/j.patrec.2005.10.010.
2. Powers, David M W (2011). "Evaluation: From Precision, Recall and F-Measure to ROC, Informedness, Markedness & Correlation" (PDF). Journal of Machine Learning Technologies 2 (1): 37–63.
3. O'Reilly, Christian and Nielsen Tore (2015). "Automatic sleep spindle detection: benchmarking with fine temporal resolution using open science tools" Front. Hum. Neurosci., 24 June 2015 | http://dx.doi.org/10.3389/fnhum.2015.00353 [3]

Kros-walidacja

Generalizacja: O co tu chodzi?

Schemat ilustrujący koncepcję generalizacji

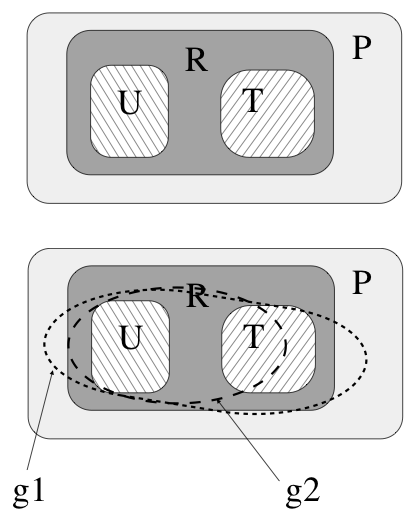
Na rysunku obok przedstawiona jest schematycznie koncepcja generalizacji. Wyobraźmy sobie, że jest pewna przestrzeń P, która zawiera pary, np. liczb {((a,b), c)}. W tym przykładzie jest to przestrzeń wszystkich odwzorowań [math]\mathcal{R}^2 \rightarrow \mathcal{R}[/math]. Niektóre z tych par reprezentują pewną konkretną relację R: np. są to pary spełniające warunek [math]c=\sqrt{a^2 +b^2}[/math]. Wyobraźmy sobie dalej, że mamy dane dwa skończone zestawy par, które tą relację spełniają, ale oczywiście nie są w stanie obejmować wszystkich możliwych par. Jeden z nich oznaczymy U, a drugi T. Załóżmy, że mamy dwie wersje sieci, które uczymy na zbiorze U (mogą się one różnić architekturą, albo punktem startu procedury uczącej, albo ilością iteracji algorytmu uczącego itp.). Po procesie uczenia sieci te mają mały i porównywalny błąd na zbiorze U, ale jedna z nich nauczyła się relacji wskazanej na rys. jako g1 a druga relacji g2. Na podstawie rezultatów odtwarzania przykładów ze zbioru testowego mówimy, że sieć druga ma gorszą generalizację niż sieć pierwsza.

Porównywanie klasyfikatorów na podstawie błędów generalizacji.

Najlepiej byłoby mieć możliwie mały błąd generalizacji — jak go oszacować? Można zastosować następujące techniki:

• wiele zbiorów testowych: trzeba mieć dużo danych, żeby wystarczyło na rozsądny zbiór treningowy i kilka testowych
• kros-walidacja: najprostsza wersja (leave-one-out):
  • wybierz przypadek do odrzucenia
  • trenuj klasyfikator na wszystkich przypadkach oprócz tego jednego — na tym jednym oblicz błąd generalizacji
  • powtarzaj to dla każdego przypadku
    Zaleta — można efektywnie użyć całego zbioru danych do uczenia i testowania,
    Cena — wielokrotne uczenie sieci