WnioskowanieStatystyczne/Testy permutacyjne
Wnioskowanie_Statystyczne_-_wykład
Spis treści
Testy permutacyjne
Jednym z najczęstszych zastosowań statystyki jest pytanie o istotność różnicy. Omówimy je na następującym przykładzie:
Przykład
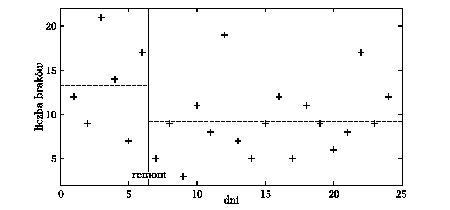
Linia produkcyjna mikroprocesorów w kolejnych dniach dawała następujące liczby wadliwych elementów: 12, 9, 21, 14, 7, 17. W związku z tym dokonano remontu, po którym przez pierwsze sześć dni liczby braków wyniosły: 5, 9, 3, 11, 8, 19. Czy na podstawie tych danych można stwierdzić, że remont zmniejszył średnią ilość braków?
Na początek obliczmy średnie liczby braków na dzień: średnia z dni przed remontem wynosi około 13,3, a z dni po remoncie — 9,2. Jak widać, druga średnia jest mniejsza o ponad 4, ale może to tylko dzieło przypadku? Wszak wśród dni „po remoncie” zdarzają się liczby braków większe niż w „lepszych” dniach sprzed remontu — tak duży jest rozrzut tych wyników. Jak ocenić istotność tej różnicy?
Załóżmy, że remont linii produkcyjnej nie miał żadnego wpływu na ilość wypuszczanych braków. Wtedy obydwie otrzymane serie będą wynikiem tego samego procesu. Inaczej można powiedzieć, że oba zestawy liczb zostały wylosowane z tej samej populacji. Co je tak naprawdę rozróżnia? Jedne z tych liczb przypisane są do stanu „przed remontem”, a drugie — „po” (zakładamy, że kolejność ich występowania nie ma tu znaczenia). Inaczej możemy powiedzieć, że dysponujemy zestawem dwunastu liczb oraz ich przypisaniem do stanu „przed” lub „po” — określmy te stany jako A i B:
| liczba | 3 | 5 | 7 | 8 | 9 | 9 | 11 | 12 | 14 | 17 | 19 | 21 |
| stan | B | B | A | B | B | A | B | A | A | A | B | A |
Jeśli uznamy, że remont nic nie zmienił, to liczby przypisane do stanu „po remoncie” (B) możemy uznać za wylosowane z tej samej populacji, co liczby przypisane do stanu „przed remontem” (A). A skoro losowanie jest przypadkowe, to różnice wartości średnich tych dwóch zestawów liczb mogą przyjmować przeróżne wartości. Na ile prawdopobne jest losowanie, w którym różnica wartości średnich wyniesie 4,2 lub więcej? Według wniosków z rozdziału Monte Carlo należy powtórzyć wiele takich losowań, i prawdopodobieństwo obliczyć jako proporcję. A skoro nie możemy powtarzać losowań z całej populacji, to zgodnie z wnioskami z rozdziału o Bootstrapie będziemy losować z dostępnej nam próby.
Proces losowania będzie polegał na wrzuceniu wszystkich dwunastu liczb do jednego worka, i wyciąganiu z niego (bez zwracania) sześciu przypadkowych, które zaliczymy do stanu A. Pozostałe w worku sześć liczb zaliczymy do B, po czym obliczymy różnicę wartości średnich.
Liczba sposobów, na które można wylosować sześć liczb z dwunastu, wynosi 924.[1] W tym przypadku nie musimy więc losować „na ślepo” — możemy po prostu sprawdzić wszystkie możliwe przypisania tych liczb stanom A i B. Dla każdego z tych przypisań obliczymy różnicę średnich w zbiorach A i B. Rozkład tych różnic będzie odpowiadać założonej w hipotezie sytuacji, w której między stanami A i B (przed i po remoncie) nie występuje żadna różnica (w liczbie braków), a podział na grupy jest sztuczny (przypadkowy).
Jak te liczby obejrzeć? Nie mamy już do czynienia z sytuacją, w której wynik przyjmuje wyłącznie wartości całkowite, jak na rysunkach z rozdziału o metodzie Monte Carlo i Bootstrapie. Potrzebny będzie nowy sposób prezentacji.
Histogram
Ten sposób prezentacji dużych ilości danych jest bezpośrednim rozszerzeniem idei używanej dotychczas do prezentacji danych dyskretnych (np. liczb wyrzuconych oczek) na przypadek ogólny (ciągły), gdy dane przyjmują dowolne wartości:
Odcinek pomiędzy najmniejszą i największą z wartości przeznaczonych do prezentacji dzielimy na równe przedziały i zliczamy liczbę wyników mieszczących się w każdym z przedziałów.
Oczywiście pojawia się pytanie, na ile przedziałów powinniśmy podzielić zakres zmiennej, gdyż histogramy tych samych danych dla różnych szerokości przedziałów będą oczywiście wyglądały inaczej. W razie wątpliwości warto obejrzeć histogramy dla kilku różnych szerokości i kierować się zdrowym rozsądkiem. Więcej uwag i przepisów dotyczących doboru optymalnej szerokości przedziału histogramu można znaleźć np w "Statystyce dla studentów kierunków technicznych i przyrodniczych" Koronackiego i Mielniczuka.
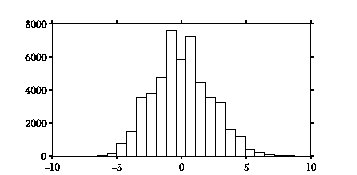
Większość otrzymanych różnic (rysunek %i 2) gromadzi się wokół zera — zgodnie z oczekiwaniami, skoro grupy losujemy przypadkowo z tej samej populacji. Jednak pomimo to widać, że w wielu przypadkach losowanie prowadzi do powstania całkiem dużej różnicy, znacznie przekraczającej otrzymane przez nas 4,2.
Dokładnie 105 (na 924 możliwych) przypadków daje wartości różnic średnich grup większe lub równe 4,2. Odpowiada to prawdopodobieństwu 0,11, czyli średnio w 11 przypadkach na sto — bez dokonywania żadnego remontu — zapisując dwie serie liczb braków w kolejnych sześciu dniach, możemy uzyskać nie mniejszą różnicę średnich. I to jest właśnie poprawne sformułowanie ostatecznego wyniku — choć zwykle używa się "mądrzej" brzmiących terminów. Spróbujemy je "oswoić" w następnym rozdziale.
Weryfikacja hipotez statystycznych — terminologia
Podsumujmy opisane powyżej postępowanie z użyciem "oficjalnej" terminologii:
- analiza problemu doprowadziła nas do sformułowania hipotezy (zwanej zwykle "hipotezą zerową") o domniemanym braku różnic między dwoma grupami liczb (A i B), odpowiadającymi liczbom braków w kolejnych dniach przed i po remoncie; przyjęcie tej hipotezy odpowiada stwierdzeniu braku efektywności remontu, zaś jej zaprzeczenie potwierdza istotne zmniejszenie liczby braków,
- jako miarę badanego efektu ("statystykę testową") wybraliśmy różnicę wartości średnich grup A i B,
- dla hipotezy zerowej rozkład tej statystyki odpowiadał będzie przypadkowym różnicom między średnimi z dowolnych dwóch sześciodniowych okresów, nie rozdzielonych remontem,
- rozkład tej statystyki (w populacji składającej się ze wszystkich możliwych zestawów liczb braków A i B zliczanych w tym samym stanie działania linii produkcyjnej) oszacowaliśmy, obliczając jej wartości dla wszystkich możliwych podziałów danych, którymi dysponujemy, na dwie sześcioelementowe próby,
- uzyskany histogram (rys. %i 2) określa rozkład wybranej statystyki testowej w przypadku, gdy prawdziwa jest hipoteza braku różnic między grupami,
- najbardziej prawdopodobną wartością dla tej statystyki jest oczywiście zero, ale, jak widać, również wartości większe od uzyskanej w analizowanym przypadku (4,2) zdarzają się całkiem często — w 105 przypadkach na 924 możliwe sposoby "pomieszania" dostępnych danych.
Poziom istotności testu
Wróćmy do postawionego na początku tego rozdziału pytania o istotność różnicy średniej liczby braków przed i po remocie. Odpowiedź na to pytanie jest dość złożona. Jednak pomimo to, zwykle oczekuje się od statystyki (statystyków) "konkretnej" odpowiedzi.
Aby takiej odpowiedzi udzielić, musimy się najpierw zdecydować, jaki błąd możemy popełnić. Za miarę badanego efektu przyjęliśmy różnicę średnich, ale jak widać duże różnice średnich (czyli wartości statystyki) mogą również wyniknąć z przypadku. Jeśli uznamy, że różnica 4,2 świadczy o tym, że grupy nie pochodzą z tej samej populacji, to musimy być świadomi, że w 11% przypadków grupy pochodzące z tej samej populacji mogą dać różnice co najmniej tak duże. Jest to prawdopodobieństwo odrzucenia hipotezy prawdziwej.[2]
Zwykle postępujemy odwrotnie:
- Najpierw ustalamy poziom istotności testu, czyli dopuszczalne prawdopodobieństwo odrzucenia hipotezy prawdziwej. Najczęściej przyjmuje się w tym miejscu 5% lub 1%, ale liczby te nie są wcale jakimiś wyróżnionymi wielkościami: pierwsza z nich dopuszcza pomyłkę w jednym przypadku na dwadzieścia, a druga — w jednym na sto.
- Dla dalszych kroków niezbędna jest znajomość rozkładu wybranej statystyki dla testowanej hipotezy. W tym przypadku hipotezą jest brak różnic, czyli losowanie obu grup z jednej populacji, a rozkład różnicy średnich przybliżyliśmy metodą właściwą dla testów permutacyjnych.
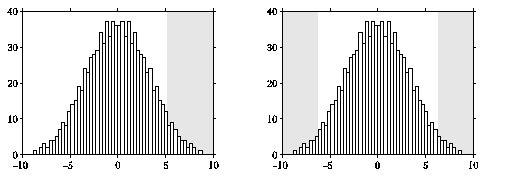
- Poziom istotności testu wyznacza obszar krytyczny statystyki, czyli takie wartości statystyki (w tym przypadku różnicy wartości średnich), dla których odrzucimy hipotezę (o braku różnic). Jeśli poziom istotności ustalimy na 5%, co odpowiadało około 45 przypadkom z 924, to obszar krytyczny będzie na prawo od wartości 5,2 — właśnie 45 przypadków ze wszystkich 924 daje wartości statystyki (różnicy średnich) większe niż 5,2. Przedział na lewo od tej wartości krytycznej stanowić będzie w tym przypadku obszar akceptacji. Na rysunku %i 3 ciemniejszym tłem zaznaczono obszar krytyczny.
- Ponieważ zaobserwowana przez nas wartość statystyki, czyli różnica średnich liczb braków przed i po remoncie (4,2) leży w obszarze akceptacji, stwierdzamy, że na poziomie istotności 5% hipotezę o braku różnic.
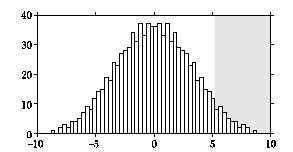
Pojęcie obszaru krytycznego i obszaru akceptacji pochodzą z teorii klasycznej, w której rozkłady prawdopodobieństwa opisane są zwykle w postaci funkcji, a nie histogramów. Tutaj właściwie możemy się bez nich obejść, gdyż łatwiej obliczyć od razu proporcję liczby przypadków, dla których statystyka przekracza wartość uzyskaną w badanym przypadku (w tym przykładzie 4,2). Odpowiada to największemu poziomowi istotności, na którym możemy zaakceptować hipotezę. Jeśli jest ona mniejsza od założonego na początku poziomu istotności testu (np. 5%) hipotezę odrzucamy.
Testy permutacyjne dla większych liczebności
Z wykonanych obliczeń wynika, że hipotezę o braku różnic między liczbami braków przed i po remoncie możemy przyjąć na założonym poziomie istotności 5%[3]. Czyli posiadane dane nie pozwalają na stwierdzenie, że remont zmienił średnią ilość wypuszczanych braków. Co można zrobić w tej sytuacji?
Można zebrać więcej danych. Liczby pomiarów sprzed remontu nie da się już niestety zwiększyć, pozostaje śledzić wyniki w kolejnych dniach po remoncie.
Dla dokładniejszego sprawdzenia hipotezy z przykładu 19, zmierzono liczby braków w dwunastu następnych dniach po remoncie. Wyniosły one: 7, 5, 9, 12, 5, 11, 9, 6, 8, 17, 9 i 12. Daje to, w sumie z poprzednimi, 18 pomiarów po remoncie i 6 przed: przed remontem: 12, 9, 21, 14, 7, 17; po remoncie: 5, 9, 3, 11, 8, 19, 7, 5, 9, 12, 5, 11, 9, 6, 8, 17, 9 i 12.
Co można powiedzieć o wyniku remontu w świetle tych danych?
Na początek raz jeszcze obliczmy różnicę średnich liczb braków przed i po remoncie. Uzyskujemy dokładnie ten sam wynik co poprzednio: 4,2. Jednak różnica wartości średnich nie jest jedyną informacją, która decyduje o istotności różnic między grupami — ważne jest to, czy wartość taka mogła się pojawić "przypadkiem".
Spróbujmy więc zastosować raz jeszcze opisany w poprzednim rozdziale test różnic. Razem mamy 24 liczby; liczba sposobów, na które możemy podzielić 24 elementy na zbiory sześcio- i osiemnastoelementowy, wynosi ponad 130 tysięcy. Dla oceny prawdopodobieństwa nie jest konieczne zbadanie rozkładu różnic dla wszystkich możliwych kombinacji — wystarczy ich część. Musimy tylko pamiętać, aby wybrana część była reprezentatywną próbą populacji wszystkich możliwych przypisań -- zapewni to przypadkowy proces losowania.
Powtórzmy raz jeszcze ogólny schemat:
- ustalamy poziom istotności testu — na przykład 5%
- jako statystykę testową przyjmujemy różnicę wartości średnich w grupach,
- aby uzyskać rozkład tej statystyki:
- wszystkie wyniki (przed i po remoncie) "wrzucamy do jednego worka",
- losujemy (np. 50000 razy) bez zwracania zbiory o liczebnościach równych wejściowym (6 i 18),
- dla każdego losowania obliczamy wartość różnicy średnich (czyli wybranej statystyki),
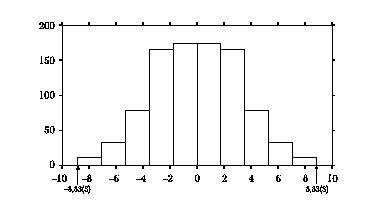
- rozkład tych wielkości (najwygodniej oglądać go na histogramie — rys. %i 5) przybliża rozkład prawdopodobieństw wystąpienia różnych wielkości różnicy średnich w przypadku słuszności hipotezy zerowej, czyli braku różnic między grupami,
- liczba losowań, w których różnica przekroczyła wartość wyliczoną dla danych wejściowych (4,2) dzielimy przez całkowitą ilość losowań; daje to maksymalny poziom istotności, na którym możemy przyjąć hipotezę o braku różnic,
- jeśli poziom ten jest mniejszy niż założony na początku poziom istotności wykonywanego testu, odrzucamy hipotezę o braku różnic między grupami.
W wyniku tej procedury dostajemy 3,8% jako maksymalny poziom istotności dla hipotezy o braku różnic. Oznacza to, że na założonym poziomie istotności 5% należy odrzucić tę hipotezę, co dowodzi istotnego zmniejszenia liczby braków po remoncie.
Test jedno- i dwustronny
Warto zwrócić uwagę na fakt, że w tym przypadku interesował nas tylko efekt zmniejszenia liczby braków w wyniku remontu (test jednostronny). Jeśli hipoteza dotyczyłaby ogólnie różnicy — dodatniej lub ujemnej — wartości średnich (test dwustronny), za podważające hipotezę o braku różnic powinniśmy uznawać również różnice o dużej wartości bezwzględnej i ujemnym znaku. Wtedy poziom istotności będzie odpowiadał sumie liczby przypadków, w których wartość bezwzględna statystyki (wartość bezwzględna różnicy średnich) przekroczyła wartość bezwzględną obserwowaną w eksperymencie. W stosunku do testu jednostronnego o tym samym poziomie istotności i rozkładzie statystyki zmieni to obszar krytyczny, tak jak na rys. %i 6.
Ile razy losować?
Opisane powyżej metody opierają się na losowaniu: prób z populacji o zadanym rozkładzie (Monte Carlo), losowaniu ze zwracaniem elementów samej próby (bootstrap) czy wreszcie losowaniu przyporządkowania elementów prób do dwóch grup (testy permutacyjne). Te losowania mają nam zastąpić wiedzę o całej populacji, czyli wszystkich możliwych wynikach takich losowań. Jednak z wyjątkiem repróbkowania niewielkich grup (w praktyce o liczebności do kilkudziesięciu elementów), wzięcie pod uwagę wszystkich możliwych kombinacji jest niemożliwe. Efekt gwałtownego wzrostu liczby kombinacji z liczebnością grupy określa się mianem "eksplozji kombinatorycznej". Prowadzi on, już dla całkiem niewielkich liczb, do szacunkowych czasów obliczeń, które mogą np. przekraczać wiek Wszechświata — bliżej opisuje to Dodatek 136.
Skoro nie można sprawdzić wszystich możliwości, to ile ich potrzeba, aby nie popełnić za dużego błędu? Cóż, można by tu posłużyć się bezpośrednio prezentowaną ideą: jeśli badamy np. poziom istotności danego testu, losując tysiąc kombinacji, sprawdźmy, na ile będą się różnić między sobą wyniki otrzymane dla kolejnych tysięcy. Jednak taka procedura (szczególnie dla większych liczb) drastycznie zwiększa koszt obliczeniowy całej operacji. Z drugiej strony, nie zawsze potrzebne nam jest dokładne oszacowanie prawdopodobieństwa.
Błąd wynikający z faktu, że nie bierzemy w obliczeniach pod uwagę wszystkich możliwych kombinacji będzie na pewno mniejszy niż błąd, który możemy popełnić stosując w ogóle nieadekwatną do danego problemu metodę.[4] Wiadomo też, że błąd będzie tym mniejszy, im większa liczba losowań. Efron i Tibshirani podają w klasycznej pracy, że dla testów permutacyjnych liczba powtórzeń powinna wynieść "przynajmniej tysiąc"; zależy to oczywiście również od tego, na jakim poziomie istotności chcemy badać hipotezę.
Dla określania błędów za pomocą bootstrapu, ci sami autorzy sugerują wartości między 50 a 200. Jednak wybór ten opierają głównie na swoich doświadczeniach, gdyż w tym przypadku dokładny szacunek błędu zależy od rozkładu populacji — sugerowane wartości odpowiadają rozkładom najczęściej spotykanym w praktyce. Sugerują oni jednak ostrożność i kontrolę jakości wyników, np. przez oglądanie histogramu wyników (jak na jednym z rysunków w rozdziale o Bootstrapie). Ogólnie dobrym pomysłem bywa również porównanie wyników dla różnych losowań tej samej liczby powtórzeń: rozrzut wyników przy kolejnych uruchomieniach programu z tymi samymi parametrami daje pojęcie o błędzie.
Co dalej?
Opisane powyżej przykłady ilustrują zastosowanie komputerów do rozwiązywania najczęściej spotykanych problemów statystycznych. Ich zrozumienie (i umiejętność programowania) pozwalają na samodzielne stosowanie statystyki "bez wzorów" w prostych przypadkach — pod warunkiem zachowania zdrowego rozsądku. Mogą w tym pomóc poniższe reguły:
- Najważniejszym elementem każdej analizy statystycznej jest właściwe dobranie metody (modelu, testu) do danego problemu. Opisane w tej części metody są na tyle intuicyjne, że właściwość wyboru nie powinna sprawiać wątpliwości.
- Im więcej powtórzeń (repróbkowania czy symulacji), tym mniejszy błąd procedury.
- Warto oglądać histogramy analizowanych danych.
I to już właściwie wszystko, co można osiągnąć bez użycia wzorów i odwołań do klasycznej teorii statystyki. Przy okazji uzyskaliśmy też intuicyjne wprowadzenie podstawowych pojęć — gdzie tylko było to możliwe bez nadmiernej komplikacji, odnosiliśmy się do terminologii pochodzącej z teorii klasycznej. Powinno to znacznie ułatwić zrozumienie dalszych części książki.
- ↑ Ogólny wzór na liczbę [math]k[/math]-elementowych podzbiorów zbioru [math]N[/math]-elementowego podany jest w rozdziale o rozkładzie dwumianowym.
- ↑ Dokładnie rzecz ujmując, chodzi oczywiście o prawdopodobieństwo odrzucenia hipotezy zerowej w przypadku, gdy jest prawdziwa.
- ↑ Najczęściej przyjmuje się poziom istotności 5% (czasem dla wykazania ewidentnych różnic, 1% lub 0,1%), choć teoretycznie powinien on być świadomie wybierany dla każdego przypadku.
- ↑ Taki "bardzo gruby" błąd jest zaskakująco częsty wśród nie-statystyków, zmuszonych do stosowania metod statystycznych.