Uczenie maszynowe i sztuczne sieci neuronowe/Wykład Ocena jakości klasyfikacji

Kross-walidacja

Porównywanie klasyfikatorów na podstawie błędów generalizacji.

Najlepiej byłoby mieć możliwie mały błąd generalizacji — jak go oszacować? Można zastosować następujące techniki:

• wiele zbiorów testowych: trzeba mieć dużo danych, żeby wystarczyło na rozsądny zbiór treningowy i kilka testowych
• kross-walidacja: najprostsza wersja (leave-one-out):
  • wybierz przypadek do odrzucenia
  • trenuj klasyfikator na wzystkich przypadkach oprócz tego jednego — na tym jednym oblicz błąd generalizacji
  • powtarzaj to dla każdego przypadku
    Zaleta — mażna efektywnie użyć całego zbioru danych do uczenia i testowania,
    Cena — wielokrotne uczenie sieci
• Bootstrapowanie — wielokrotnie losuje się z powtórzeniami z pełnego zbioru dwie próby:
  • do nauki klasyfikatora
  • do testowania.

Krzywe charakterystyki roboczej odbiorcy (ROC)

Rozważmy nasz przykład klasyfikowania kandydatów na przyjętych i nie przyjętych. Możemy podjąć następujące decyzje:

		Stan faktyczny		Razem
		przyjęty	nie przyjęty
wynik klasyfikacji	przyjęty	TP	FP (błąd: wynik fałszywie pozytywny)	P'
	nie przyjęty	FN (błąd: wynik fałszywie negatywny)	TN	N'
Razem		P	N

Anglojęzyczna nomenklatura często stosowana do opisu tych możliwości to:

• TP: true positive, hit
• TN: true negative, correct rejection
• FP: false positive, false alarm, Type I error
• FN: false negative, with miss, Type II error

Miary oparte na tych definicjach to:

• czułość (inne spotykane nazwy: sensitivity, true positive rate TPR, hit rate, recall)

[math]TPR = TP / P = TP / (TP+FN)[/math]

• częstość fałszywych alarmów ( false positive rate (FPR), fall-out)

[math]FPR = FP / N = FP / (FP + TN)[/math]

• dokładność ( accuracy (ACC))

[math]ACC = (TP + TN) / (P + N)[/math]

• specyficzność: (specificity (SPC), True Negative Rate)

[math]SPC = TN / N = TN / (FP + TN) = 1 - FPR [/math]

• precyzja: (positive predictive value (PPV), precision)

[math]PPV = TP / (TP + FP)[/math]

• negative predictive value (NPV)

[math]NPV = TN / (TN + FN)[/math]

• częstość fałszywych odkryć: (false discovery rate (FDR))

[math]FDR = FP / (FP + TP)[/math]

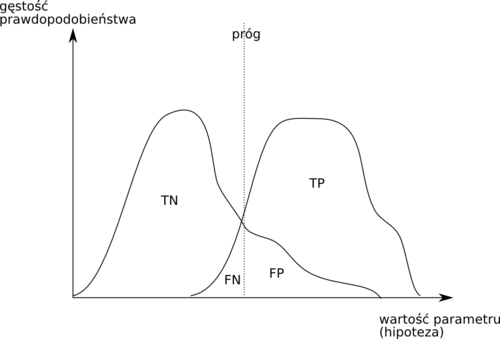
Prawdopodobieństwa podejmowania każdego rodzaju decyzji będą się zmieniały wraz z przesuwaniem progu podejmowania decyzji, czyli wartości hipotezy przy której zaliczamy przypadek do klasy 1.

Krzywa ROC

każdy punkt na tej krzywej otrzymywany jest dla ustalonej wartości progu i ma współrzędne (1−specyficzność, czułość).

Krzywa ROC przydaje się do porównywania różnych klasyfikatorów oraz do wyboru punktu pracy (progu)